政华公考

【答案】B【解析】首先我们需要注意，小芳喝的这65瓶水包括小芳她自己花钱买的和通过兑换得到的。因此，如果我们设小芳花钱买了x瓶水，并且题干中的“8个空瓶可以换一瓶水”，我们用等式来表示可以写成：8个矿泉水空瓶=1瓶矿泉水=1个矿泉水空瓶+1份水（一份水不包括空瓶），可以得：7个矿泉水空瓶=1份水。则小芳通过兑换可以得到x÷7瓶水，因此可以得到x+x÷7=65，解得x=56.875，即至少买56.875瓶水加上兑换的才能保证小芳这个月喝了65瓶，而矿泉水瓶数只能是整数，因此在不小于56.875的整数里选择最小的57，答案选B。

总结：当我们已知规则及喝到的瓶数，求至少应买多少瓶水时，我们只需要利用换水规则列方程求解即可。只不过需要注意的是，当未知数解出来为非整数时，我们需要向上取整。

基本原理

我们通过下面这一道题目来探究一下这类题目的通用解法。

例1：3个空啤酒瓶可以免费换一瓶啤酒，现有32个啤酒空瓶，请问最多可以免费喝多少啤酒（）？

A.13 B.14 C.15 D.16

【答案】D【解析】很多同学拿到这类题目，往往就是一步一步地去换：

第一步：32个空瓶可以拿出30个空瓶来换10瓶啤酒，还剩2个空瓶；

第二步：把这10瓶啤酒喝掉可以得到10个空瓶，那么就一共有12个空瓶，再拿去换4瓶啤酒；

第三步：把这4瓶啤酒喝掉可以得到4个空瓶，拿出3个空瓶换1瓶啤酒，这时还剩下1个空瓶；

第四步：把这1瓶啤酒喝掉可以得到1个空瓶，一共就有了2个空瓶。2个空瓶看似不够换一瓶，但实则我们可以借1个空瓶过来，凑够3个空瓶，换得1瓶啤酒喝掉后再把借来的这1个瓶子还掉就可以了。

这样一共可以免费喝10+4+1+1=16瓶，故选择D选项。

但这个方法非常浪费时间，而且最后这个瓶子是需要借的，很多同学想不到这点。所以为大家带来一种更快解题的方法：

解析：根据题意3个空瓶=1瓶啤酒，我们可以把这1瓶啤酒看成1个空瓶加1份酒，得到3个空瓶=1个空瓶+1份酒，那么等式两边的1个空瓶可以消掉，变成2个空瓶=1份酒，也就是有2个空瓶就可以喝1份酒，那么32个空瓶就可以喝32÷2=16瓶酒，故选择D项。

【模型特征】：已知兑换规则及空瓶数，求最多能喝到的瓶数。

【基本公式】：假设n个空瓶可以换一瓶水，那么m个空瓶最多可以喝到m÷（n-1）瓶水。

灵活考法

为了让大家能够更好地掌握这类题型，我们再一起来了解一下它常见的变形。

例2：某啤酒开展“12个空瓶换1瓶啤酒”的大型促销活动，小张和他朋友在活动期间共喝了245瓶啤酒，那么他们至少需要买多少瓶啤酒？（）

A.223 B.224 C.225 D.226

【答案】C【解析】根据题意小张和他朋友喝的245瓶啤酒包括了花钱买的和通过兑换得到这两部分。因此这道题本质上还是空瓶换水的思路：将一瓶啤酒看成1个空瓶+1份酒，所以根据兑换规则得到12空瓶=1空瓶+1份酒，也就是11空瓶=1份酒，设买了x瓶水，可得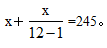：解得想x≈224.6，因为x为正整数且最少为224.6，所以n向上取整为225，故选择C项。

通过这道题可以得到空瓶换水问题的变形总结：已知兑换规则及喝到的水数，求至少买多少瓶。这类题目只需要利用兑换规则列方程求解即可。值得注意的是当未知数解出来为非整数时，记得取整。

例题3：若5个矿泉水空瓶可以免费换1瓶矿泉水，现有132个矿泉水空瓶，最多可以免费喝到几瓶矿泉水？（）

A.31瓶 B.32瓶 C.33瓶 D.34瓶

【答案】C【解析】拿到这道题，很多同学估计已经开始在草稿纸上演算了，一步一步地去换水。先拿132个空瓶去换水，可以换132÷5=26…….2，即换26瓶水且余2个空瓶；26瓶水喝完又有26个空瓶，和之前剩余的2个空瓶此时共有28个空瓶。28个空瓶又可以换28÷5=5……3，即换5瓶水且余3个瓶子；以此类推，8÷5=1……3，此时喝完1瓶水得到1个空瓶，加上剩余的3个空瓶，一共有4个空瓶，到这一步有同学就想手里的瓶子已经不够换水了，那么一共喝到了26+5+1=32瓶。遗憾的是，经过这样一步一步繁琐的过程最终还是做错了，实在可惜。

为什么呢？这样思考本身没有问题，但是易错的地方是最后4个空瓶能否换水呢？此时差一点就可以换到水了，不换岂不有点可惜？那能否想办法换到呢？就差一个空瓶而已，试想一下，我们可否借一个空瓶，那么我们就凑齐了5个空瓶，此时便可换到1瓶水，喝完有1个空瓶，正好可以还回去，两全其美，何乐而不为呢？这样一想，我们完全还可以再喝到1瓶水的，所以我们最多可以喝到33瓶水，正确答案应该选C项。

经过上面这样一步步地思考兑换的过程，我们不难发现，这样去做空瓶换水类的题目太过繁琐，而且一不小心容易出错，那么有没有技巧可以帮助我们避免错误，而且能快速做对类似的题目呢？肯定是有的。实际上，我们根据题干中的交换规则“5个空瓶子换1瓶水”，可得“5空瓶=1瓶水=1空瓶+1份水”，化简为“4空瓶=1份水”，所以最多能免费喝到132÷4=33瓶水，故选择C选项。

结论：若n个空瓶换1瓶水，则n-1个空瓶=1份水。

例题4：某啤酒厂为促销啤酒，开展6个空啤酒瓶换1瓶啤酒的活动，孙先生去年花钱先后买了109瓶该品牌啤酒，期间不断用空啤酒瓶去换啤酒，请问孙先生去年一共喝掉了多少瓶啤酒？（）

A.127瓶 B.128瓶 C.129瓶 D.130瓶

【答案】D【解析】根据题干信息，6个空瓶=1个空瓶+1份啤酒，则5个空瓶=1份啤酒，孙先生买了109瓶该啤酒，也就有109个空啤酒瓶，因此109个空啤酒瓶最多可以换到啤酒109÷5=21.X瓶，所以孙先生去年一共喝掉109+21=130瓶啤酒，故本题选D。

通过上面两道题目，大家不难发现空瓶换水类题目易掌握、易得分，每位同学都可以快速掌握，只要考到了，直接套用公式就可以轻松解决。

空瓶换水里的数学思维

例1：某商店节日促销，以“回收环保，以3换1”的主题售卖饮料。具体规定如下：3个同款饮料空瓶可以免费换1瓶同款饮料。一瓶饮料售价5元。李红现有30元，最多可以喝到几瓶饮料？（）

A.9 B.8 C.6 D.10

【答案】A【解析】易错点：李红首先可以用30元买6瓶饮料，喝完饮料以后得到6个空瓶。这6个空瓶还可以换2瓶饮料，再喝完会剩下2个空瓶，不满足“以3换1”的条件。所以一共可以喝到8瓶饮料。选择B项。但这并不是最优方案，为什么呢？

思路一：其实大家忽略了一种情况，李红可以先向商店“借”1个空瓶，这样加上之前剩下的2个空瓶，就凑够了3个空瓶，再去换一瓶饮料喝掉，最后把喝掉剩下的空瓶还给商店，能够达到“借1还1”的状态。这种数学思维能够达到最多喝9瓶饮料的结果。选择A项。

思路二：思路一可以达到最多的情况，但是只限数值较小的题目，如果这道题变成李红有100元，甚至更多钱，一点一点的推理会非常耗费时间，同时还需要考虑剩下的瓶子、换了以后的瓶子、借瓶子的情况等等。所以接下来的方法才是大家学习的重点。

最终我们需要的是最多能喝多少瓶饮料，所以可以从替换关系入手分析。3个空瓶=1瓶饮料→3个空瓶=1个空瓶+1份饮料（没有瓶子装的饮料）→2个空瓶=1份饮料。这样的替换关系就可以忽略再次换饮料以后还会留下空瓶的过程。现在李红有30元，可以先买30÷5=6瓶饮料，得到6份饮料和6个空瓶，替换关系为2个空瓶=1份饮料，所以其中的6个空瓶=3份饮料，最终最多可以喝到6+3=9份饮料。选择A项。

例2：某商店节日促销，以“回收环保，以5换1”的主题售卖饮料。具体规定如下：5个同款饮料空瓶可以免费换1瓶同款饮料。一瓶饮料售价5元。李红现有100元，最多可以喝到几瓶饮料？

A.20 B.24 C.25 D.26

【答案】C【解析】5个空瓶=1瓶饮料→5个空瓶=1个空瓶+1份饮料（没有瓶子装的饮料）→4个空瓶=1份饮料。现在李红有100元，可以先买100÷5=20瓶饮料，得到20份饮料和20个空瓶，替换关系为4个空瓶=1份饮料，所以其中的20个空瓶=5份饮料，最终最多可以喝到20+5=25份饮料。选择C项。

如何巧解此类题目

例1：某商店为了吸引顾客做一个促销活动，每3个空汽水瓶可以换一瓶汽水，问：小张共有11个空瓶最多可以喝到几瓶汽水？（）

【解析】（1）基本方法：由于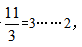可知能换到3瓶汽水还剩2个空瓶，3瓶汽水喝掉后再加剩余的2个空瓶，可得到5个空瓶。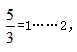能换到1瓶汽水还剩2个空瓶，1瓶汽水喝掉可得到3个空瓶，又能换到1瓶汽水，最终共喝到3+1+1=5瓶汽水。

（2）巧解方法：明确题目中的核心兑换规则，3个空瓶换1瓶汽水，也就是3空瓶=1瓶水=1空瓶+1份水，即2空瓶=1份水。因此，直接用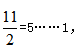最多能喝到5瓶汽水。

【解题方法】直接套用公式——已知规则及空瓶数，问最多能喝到水的瓶数。

例2：若12个空瓶可以免费换1瓶汽水，现有101个空瓶，最多可以免费喝到几瓶汽水？

A.8瓶B.9瓶C.10瓶D.11瓶

【答案】B【解析】明确题目中的兑换规则，12个空瓶换1瓶水，即12空瓶=1瓶水=1空瓶+1份水，即11空瓶=1份水。因此所求为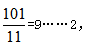最多能喝到9瓶汽水。

例3：商店开展“7个空瓶换一瓶啤酒”的优惠活动。已知张先生在活动促销期间共喝掉347瓶“红星”啤酒，问张先生最少买多少瓶啤酒？（）

A.296 B.298 C.300 D.302

【答案】B【解析】明确题目中的兑换规则，7空瓶=1瓶酒=1空瓶+1份啤酒，即6空瓶=1份啤酒。此时设张先生最少需要买x瓶啤酒，则换回酒的份数为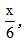由题可得：此时需要分析x的取值，x假设为最少，而啤酒的瓶数一定是整数，需要向上取整，因此最少需要买298瓶啤酒，故选择B选项。

【解题方法】间接套用公式——已知规则及喝到水的份数，求至少应买多少瓶水。

以上即为空瓶换水的巧解方法。以后解决此类问题时，首先需要明确题目中的兑换规则，将兑换规则转化为a空瓶=b份水的形式，再进行求解即可。此类问题在考试中的考查形式相对来讲比较单一，同学们只要明确方法，相信可以轻松解决。