政华公考

【答案】D【解析】本题中要将10名专家安排到10个房间，且每间安排一人。在安排过程中提到两个要求：1.4人要求住2层，2.3人要求住1层。这两个要求就体现了我们说的“有绝对限制条件的元素”。因此我们考虑用优限法解决。共有10人，其中4人要求住2层，从二层的5个房间中选出4个，安排4人入住，其方法数为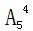，3人要求住一层，从一层的5个房间中选出3个，安排3人入住，其方法数为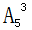，其余3人安排住剩下的3个房间，其方法数为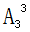，故共有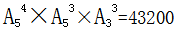种不同的安排方案。

2.捆绑法

适用环境：题干中要求元素相邻或者位置相邻时，考虑捆绑法。

具体操作：先考虑整体的顺序要求，再考虑整体内部的顺序要求。

【例2】为加强机关文化建设某市直机关在系统内举办演讲比赛3个部门分别派出3、2、4名选手参加比赛，要求每个部门的参赛选手比赛顺序必须相连，问不同的参赛顺序的种数在以下哪个范围之内（）？

A.小于1000 B.1000-5000 C.5001-20000 D.大于20000

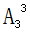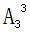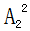【答案】B【解析】本题中要安排3个部门中参赛选手的演出顺序。在安排过程中要求每个部门的参赛选手比赛顺序必须相连。这个要求体现了我们说的“元素相邻”，考虑用捆绑法，首先将三个部门的选手看成3个整体，考虑三个整体的出场顺序，有=6种；其次考虑每个整体内选手的出场顺序，分别有=6种，=2种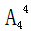，=24种。则不同参赛顺序的种数为6×6×2×24=1728，计算结果显然大于1000小于5000，故此题答案为B。

3.插空法

适用环境：题干中要求元素不相邻时，考虑插空法。

具体操作：先安排其他元素的位置，再将不相邻的元素插空安排。

【例3】由数字1、2、3、4、5组成无重复数字的五位数，两个偶数互不相邻的五位数有几个？

【答案】72个【解析】本题中要用1-5个组成无重复数字的五位数，组数过程中要求两个偶数互不相邻，这体现了我们说的“要求元素不相邻”，考虑用插空法。先安排剩余的3个奇数，有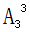=6种，再从奇数形成的4个空位中选2个空将剩余的2个偶数放入，有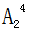=12种，因此所求为6×12=72个。

4.间接法

如果题目直接考虑需要分类比较多，而它的对立面包含情况比较少方便计算，我们可以用总方法数减去对立面方法数进行计算。

练习题

例1：五名优秀组员按顺序做年终总结报告，小张只能第一个或最后一个作报告，一共有多少种报告顺序（）？

A.24 B.36 C.48 D.60

【答案】C【解析】分析题目，其中对于小张而言，有绝对的位置限制，那么这道题应该采用优限法来解题，要优先考虑小张的位置。由于小张只能第一个或最后一个作报告，那他只能从这两个位置中选一个，有2种选择方法。对于其他人而言，题目没有任何限制，那剩余的4人可以任意选择报告位置，有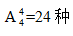选择方法，所以共2×24=48种报告顺序，结合选项，答案就是C。

例2：五名优秀组员按顺序做年终总结报告，同部门的小张和小李顺序相邻，一共有多少种报告方式（）？

A.24 B.36 C.48 D.60

【答案】C【解析】分析题目，小张和小李相邻作报告，所以这道题应该采用捆绑法来解答。假设将小张与小李捆绑在一起，则小张与小李作报告顺序一定相邻。将小张和小李看作一个整体，与剩余三人进行排序，共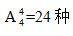报告顺序，但是小张与小李两个人之间也要排序，共2种报告顺序。所以一共有24×2=48种报告顺序，所以答案选C。

例3：五名优秀组员按顺序做年终总结报告，同部门的小张和小李顺序不能相邻，一共有多少种报告顺序（）？

A.64 B.72 C.86 D.98

【答案】B【解析】分析题目，小张和小李不相邻，所以这道题应该采用插空法来解答。插空法的使用原则是先将没有要求的人的顺序排好，再将小张和小李插入这些人形成的空隙中，则小张和小李自然不相邻。根据这个方法，除小张与小李外，还有3个人，3个人排序方法有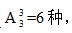3个人形成了4个空位，再从4个空位中选两个出来让小明和小红去插入，有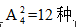顺序，则总的报告顺序有6×12=72种。故答案选B。

例4：某交警大队的16名民警中，男性为10人。现要选4人进行夜间巡逻工作，要求男性民警不得少于2人，问：有多少种选人方法？

A.1605 B.1520 C.1071 D.930

【答案】A【解析】男性民警为10人，则女性民警有6人。现要选四人且男性民警不得少于两人，所以采用间接法，则男民警可以有2人、3人、4人，这三类情况，情况数较多，考虑对立面，男性民警少于2人，即没有男性民警或只有1名男性民警，两类情况，所以我们可以用总的情况数-1男3女的情况数-0男4女的情况数求解，则本题所求为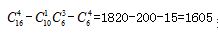种。故本题选A。

排列组合之隔板模型

一、隔板模型的含义及基本公式

隔板模型，即将n个相同元素分给m个不同对象，要求元素全部分完，且每个对象至少分一个元素的模型，可见下题：

例1：现有7个一样的苹果，要分给3个小朋友，每人至少分1个，请问有多少种分法？

【解析】题目要求把7个一样的苹果分给3个小朋友，每人至少分1个。可理解为将7个苹果摆成一排，在中间的6个空中选2个空分别放隔板。此时将苹果分为3堆，对应3个小朋友分到的苹果，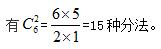

由上题，我们也可以总结出隔板模型的基本公式：将n个相同元素分给m个不同对象，要求元素全部分完，且每个对象至少分一个元素，方法数为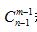种。

二、隔板模型的灵活应用

1.变式一：将n个相同元素分给m个不同对象，要求元素全部分完，且每个对象至少分n个元素。考虑先给每个对象分n-1个元素，再利用基本公式求解。

例2：10个苹果分给3个人，每人至少分2个，有多少种分法？

【解析】10个苹果分给3个人，每人至少分2个。考虑先给每人分1个苹果，那么还剩下7个苹果。问题转化为继续将7个苹果分给3个人，每人至少分1个。根据隔板模型基本公式，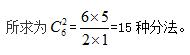

2.变式二：将n个相同元素分给m个不同对象，要求元素全部分完，任意分配。考虑先从每个对象分别借一个元素，再利用基本公式求解。

例3：某幼儿园购买了15瓶饮料，要分给小明、小红、小张3名小朋友。假设这些饮料任意分配给3名小朋友，则共有多少种不同的分配方式？

【解析】15瓶饮料分给3名小朋友，每人至少分0瓶。考虑先从每名小朋友借1瓶饮料，此时共有18瓶饮料，由于要还每人1瓶，所以此题就转换成了将18瓶饮料分给3名小朋友，每人至少分1瓶。根据隔板模型基本公式，所求为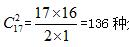分配方式。

行测数量关系隔板“变形计”

排列组合是行测考试中难度较高的一类题型，但是“相同元素分配给不同对象”这类题目有固定的解题方法，那就是“隔板模型”，只要勤加学习，此类题目求解会变得非常容易。然而在实际考试当中，出题人总是会给同学们设置障碍，对基本模型进行变形混淆大家做题的思路。下面就带大家一起来了解一下隔板模型及常见变形题目的解答方法。

例1：将15块相同的糖果分给3个小朋友，每人至少分1块，有多少种分配方法（）？

A.89 B.90 C.91 D.92

【答案】C【解析】把15块相同的糖果放成一排后，糖果间会形成14个空位，在这些空位中插入2个隔板就能将糖果分隔成3堆。因此小朋友们依次以堆为单位分掉糖果即可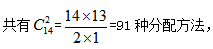，选择C项。

小结1：隔板模型：将n个相同的元素分给m个不同的对象，每个对象至少分1个，分配的方法数为：

例2：将20个相同的篮球分给4个班级，每个班级至少分2个篮球，共有多少种分配方法（）？

A.455 B.441 C.400 D.315

【答案】A【解析】本题与例1相似，但略有不同，区别在于：例1中每个对象至少分1个，而例2中每个对象至少分2个。在分配时，可以每班先分1个，共分掉4个之后，本题就转化成为“将16个相同的篮球分给4个班级，每个班级至少分1个”。所以有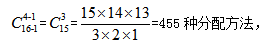选择A项。

小结2：隔板模型变形1：将n个相同的元素分给m个不同的对象，某些对象要求至少分k个元素（k≥2)，先给这些对象分k-1个元素，变型转化为每个对象至少分1个，再进行计算。

例3：将6本相同的作业本分给3名同学，每个同学都可以不分作业本，共有多少种分配方法？（）

A.28 B.36 C.40 D.48

【答案】A【解析】本题与例1相似，但也略有不同，区别在于同学可以不分作业本。因此可以先向每个同学借1本，共借到3本之后，本题就转化成为“将9本相同的作业本分给3名同学，每人至少分1本”。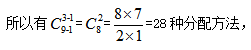选择A项。

小结3：隔板模型变形2：将n个相同的元素分给m个不同的对象，当某些对象可以不分到元素时，先向这些对象分别各借1个，变形转化为每个对象至少分1个，再进行计算。

通过上述例题的介绍，相信同学们对于结合题目的不同变形要求，正确使用隔板模型有了一定的了解。旧书不厌百回读，熟读深思子自知。希望各位同学对于题目能反复练习和琢磨，做到举一反三。