行测数量关系——几何问题详解

行测数量关系中，哪一类题型被严重低估了

众所周知，在行测数量关系考试中，每种类型的题目考查频率和难度有所不同。曾几何时，很多同学认为几何问题考查的不多而且很难，导致几何问题的价值被严重低估。

通过研究近三年省考联考行测科目考查的题型题量发现：数量关系部分均是考查了15道题目。每年都包含4道左右的几何类题目，有的是直接考查，有的是结合了概率等问题。考查的内容主要是直角三角形，相似三角形等基础知识点。以直角三角形考点为例，下面一起来看一下具体的题目。

一、考试中常对含30°和45°角的两个特殊直角三角形三边的比例关系进行考查。

例1：甲、乙、丙、丁四人通过手机的位置共享，发现乙在甲正南方向2千米处，丙在乙北偏西60°方向2千米处，丁在甲北偏西75°方向。若丁与甲、丙的距离相等，则该距离为：（   ）

【答案】B【解析】根据题干中四人的关系，作图如下，连接A、C。在△ABC中，AB=BC=2千米，∠B=60°，则△ABC是等边三角形，AC=2千米，∠BAC=60°。在△ACD中，AD=CD，∠CAD=180°-∠BAC-75°=180°-60°-75°=45°，则∠DCA=45°，∠CDA=90°，△ACD是等腰直角三角形，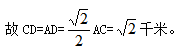

二、常见的勾股数需要掌握3、4、5；5、12、13。同时，勾股数可以等比例扩大，如3、4、5可以扩大为6、8、10。

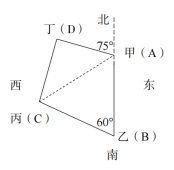
例2：小贾骑车从起点出发向东骑行3千米后，折向南骑行7千米，又向东骑行5千米后，再向北骑行1千米。现在，小贾距离起点的直线距离是多少千米（   ）？

A.6         B.8         C.10    D.16

【答案】C【解析】小贾的骑行路线如图中的线段，起点为A，终点为E，所求为AE。延长DE和AB，使两条线段相交于点F，则AF=AB+BF=AB+CD=3+5=8千米，EF=BC-DE=7-1=6千米。AF和EF为△AEF的两条直角边，由常见的勾股数可知，斜边AE=10。选C。

通过上面的两道题，我们看到实际考试时有的几何类题目难度并不高，如果直接放弃真的是很可惜。公考中每一分都很重要，取舍的同时也要尽量的抓住每个机会。

行测数量关系：神奇三角形在哪里

今天给同学们指一条解答几何问题的明路就是三角形，它的考察频率高，考点技巧通俗易懂，尤其是那神奇的三角形——直角三角形，下面一起来学习吧。

一、几何问题基础知识

1.基础知识：三角形三边关系，即两边之和大于第三边，两边之差小于第三边；三角形周长为三边之和，三角形面积为

2.勾股定理：直角三角形的两条直角边的平方和等于斜边的平方和；常考勾股数有3、4、5，5、12、13，以及成倍数的三边，如6、8、10等。

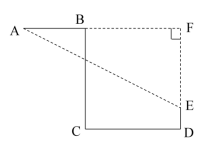
3.特殊直角三角形及三边比例关系：

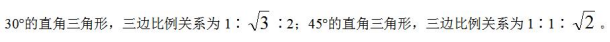
二、神奇三角形——直角三角形

同学们读完上面的内容可能会发现，这些知识点很多都和直角三角形有关系。同学们平时复习的时候可能也会发现，很多几何题目是需要求解一些规则或不规则图形的长度、两地之间距离、物体的高度等，而这些却不能直接求出。而这就需要神奇的直角三角形来帮助我们解题，接下来一起去寻找题目中的神奇直角三角形吧。

三、神奇三角形在哪里

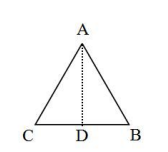
【基础练习】某正三角形边长为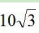，该正三角形的高为多少？

【答案】15【解析】如下图所示构造直角三角形，过A点做AD垂直于BC，垂足为D，则三角形ABD为直角三角形，且∠BAD=30°，满足三边比例为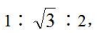，其中

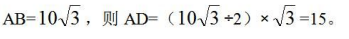
【进阶训练】一个半圆形拱门的宽和高分别为8米和4米。一辆货车拉着宽4.8米、每层高20厘米的泡沫板通过该拱门。如果车斗底部与地面的垂直距离为1.1米，问要通过拱门，每次最多可以装载几层泡沫板？（   ）

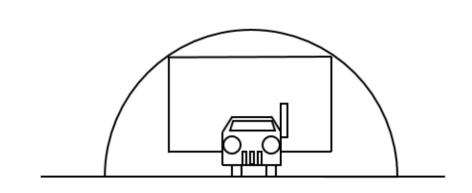
A.9        B.10            C.11        D.12

【答案】B【解析】将原图转化为如下的简易图，当泡沫板的宽正好与拱门接触时，泡沫板的高度和最大，装载泡沫板的数量最多。此时用AB表示泡沫板的宽，O为半圆圆心连接AO，则AO长为4米。过O做OC垂直于AB，垂足为C，则构造了直角三角形AOC，其中AC为AB长度的一半，即2.4米，则根据勾股定理可以求出OC=3.2米。又因为OD=1.1米，则CD=3.2-1.1=2.1米，一层泡沫板高20厘米=0.2米，2.1÷0.2=10.5，所以最多能装载10层泡沫板。故本题选B。

行测数你最“量”——几何中的相似三角形

一、相似三角形的概念

相似三角形：当两个三角形三角对应相等或三边对应成比例，则称这两个三角形为相似三角形。而在我们常见的题目中，相似三角形往往是伴随着平行出现的，比如最常见的两种相似三角形如下图所示：

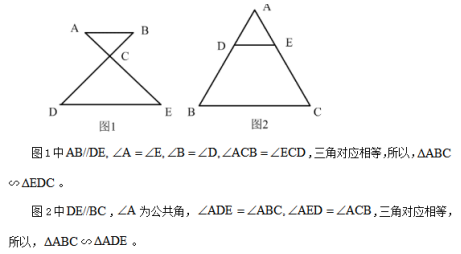
这两种相似三角形不一定单独出现，大多数情况隐藏在其他更复杂的图形里面，所以需要大家对这两种图形有一定的敏感性。

二、相似三角形的性质

1.相似比=边长比=周长比（如两三角形相似比为1：2，则周长比也为1：2）

2.相似比的平方=面积比（如三角形相似比为1：2，则面积比为1：4）

三、相似三角形的应用

我们已经了解了相似三角形的性质，接下来通过几道例题一起来感受一下相似比在题目中的应用吧。

例1：如图所示，梯形ABCD，BC的长度AD是的2倍。

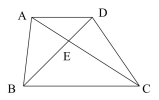
（1）△ADE与△CBE是否是相似图形？为什么？

（2）AD与CB的长度比为________，AE与CE的长度比为________，DE与BE的长度比为________。

（3）△ADE和△CBE的周长之比为________，面积之比为________

【答案】

（1）相似；因为AD∥CB，则△ADE与△CBE的三个角均相等。

（2）1∶2，1∶2，1∶2。

（3）根据相似三角形的性质，所以为1∶2，1∶4

例2：一块三角形农田ABC（如下图所示）被DE、EF两条道路分为三块。已知BD=2AD.CE=2AE.CF=2BF.则三角形ADE、三角形CEF和四边形BDEF的面积之比为：（   ）

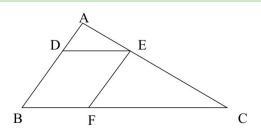
A.1：3：3           B.1：3：4           C.1：4：4         D.1：4：5

【答案】C【解析】由题意可知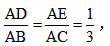，，则△ADE∽△ABC，且相似比为1：3，则△ADE与△ABC面积比为1：9；同理，则△CEF∽△CAB，相似比为2：3，△CEF与△CAB面积之比为4：9。设△ADE的面积为1，那么△ABC的面积为9，△CEF的面积为4，四边形EDEF面积为9-1-4=4，△ADE、△CEF、四边形BDEF的面积之比为1：4：4，故本题选C。

相信通过以上两道例题，各位考生对于相似三角形的应用有了更直观的认识，在做题过程中如遇到类似题目我们便可去应用相似三角形的性质进行作答。

行测数量关系几何问题——相似图形

接下来说一说几何问题中常考的一类题目——相似图形（常考相似三角形）应该如何解决。

首先我们要清楚，在行测考试中，相似图形的证明依据有两个：1.对应角相等；2.对应边成比例，两个条件满足其一即可，我们不需要那些较为麻烦的论证条件去佐证图形的相似，因此，这类题目的难度远远低于我们在初高中接触到的题目。

其次，我们需要明确，通常情况下这类题目的考察只集中在以下两个考点上：

（一）相似多边形边长比等于相似比

例1：如图所示，△ABC是直角三角形，四边形IBFD和四边形HFGE都是正方形，已知AI=1cm，IB=4cm，问正方形HFGE的面积是多少（   ）

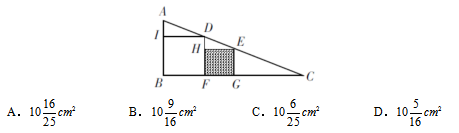
【答案】D【解析】本题中四边形 IBFD和四边形HFGE都是正方形，所以IB=ID=DF=4cm，四边形HFGE边长未知，可以设为x，因此DH=DF-HF=（4-x）cm，观察△AID和△DEH，∠DAI=∠EDH，∠ADI=∠DEH，∠AID=∠DHE，所以△AID∽△DEH，所以一定存在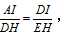代入数字得到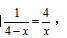交叉相乘解得x=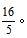所求为正方形HFGE的面积，也就是边长的平方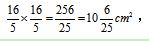，故本题选择D。

（二）相似多边形面积比等于相似比的平方

例2：一块种植花卉的矩形土地如图所示，AD边长是AB的2倍，E是CD的中点，甲、乙、丙、丁、戊区域分别种植白花、红花、黄花、紫花、白花。则种植白花的面积占矩形土地面积的：（   ）

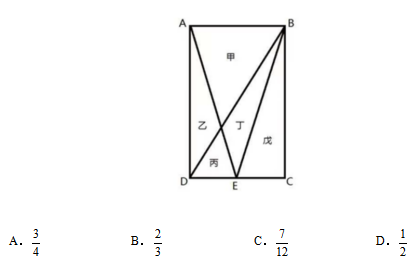
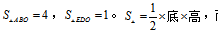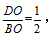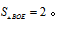【答案】C【解析】根据E为DC中点，可以得到AB：DE=2：1。设AE和BD的交点为点O，在△ABO和△EDO中，∠AOB=∠EOD，∠OAB=∠OED，所以△ABO∽△EDO，相似比为2：1，故面积之比为4：1，因此，设而△EDO和△BOE的高相同，所以面积之比等于相似比，也就是因此同理可证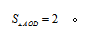△BDE和△BEC等底同高，因此面积相等，即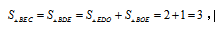因此总面积为1+4+2+2+3=12，种植白花面积“甲+成”为4+3=7，占比为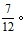。故本题选择C选项。

由上述例题可见，行测当中的相似图形的考察难度并不大，只要熟练掌握相似比与边长（周长）、面积之间的比例关系，就可以轻松解决题目，还不抓紧时间学起来！