行测技巧：数量关系的五种神奇解题方法
一、方程法
方程法是解决数量关系题目的基础方法，是数学运算的第一思维，在考试中应用广泛，也是大家必须熟练掌握的方法。解题步骤一般为，先找到题目中的等量关系，再设未知数列方程，最后解方程得到答案。方程法的核心是找等量关系，即要求我们有将文字语言转化为数学式子的能力。掌握这个方法，再辅以准确计算的能力，我们就能够稳稳拿分。
例题：社区工作人员小张连续4天为独居老人采买生活必需品。已知前三天共采买65次，其中第二天采买次数比第一天多50%，第三天采买次数比前两天采买次数的和少15次，第四天采买次数比第一天的2倍少5次。问：这4天中，小张为独居老人采买次数最多和最少的日子，单日采买次数相差多少次（ ）？
A.9 B.10 C.11 D.12
【思路梳理】
题目描述了四天的采买次数情况，可以利用前三天采买次数加和等于65这一等量关系来列方程求解。同时，这四天的采买次数都直接或间接与第一天相关，所以可设第一天采买次数为x，进而表示出其他三天的次数。
【解析】
设第一天采买了x次，根据题干条件可分别表示出其他三天的采买次数，如下表所示：
则根据前3天采买次数之和为65，可得x+1.5x+2.5x-15=65，解得x=16。即第一天采买16次，则第二天采买1.5×16=24次，第三天采买2.5×16-15=25次，第四天采买2×16-5=27次。其中采买次数最多和最少的分别是第四天（27次）和第一天（16次），两者相差27-16=11次。故本题选C。
通过这道题，大家可以看出方程法的应用难度并不高，但在解题过程中设哪一未知量为x也会影响解题的速度，所以大家在学习的过程中也要在这些细节上多下功夫。
二、整除法
除了较为基础的方程法，数量关系中还有一些优化解题步骤，提高解题速度的技巧性方法。整除就是其中非常受考生喜爱，且难度不高的一种方法。所谓整除法，是指通过题干中所给的信息，判断结果应具备的整除特性，从而帮助我们快速确定答案或排除错误答案的方法。学好整除法，核心是要培养敏感性，确保在读题过程中快速判断结果应该具有的整除特性。
例题：某老旧写字楼重新装修，需要将原有的窗户全部更换为单价90元每扇的新窗户。已知每7扇换下来的旧窗户可以跟厂商兑换一个新窗户。全部更换完毕后共花费16560元且剩余4个旧窗户没有兑换，那么该写字楼一共有多少扇窗户（ ）？
A.214 B.218 C.184 D.188
【思路梳理】
题目中出现了“每7扇换下来的旧窗户……”，结合“每”字和题目中窗户数量为正整数的背景，判断此题可尝试用整除解题。
【解析】
题目求该写字楼的窗户总数，即所有需要重新装修的旧窗户总数。由于窗户数是正整数，且“每7扇换下来的旧窗户可以跟厂商兑换一个新窗户”“全部更换完毕后……剩余4个旧窗户没有兑换”，可知窗户总数减4后是7的倍数。观察选项，只有A选项214-4=210是7的倍数。故本题选A。
整除法的使用不局限于题型，而是要关注出现整除特性的“关键词”，比如特殊的文字“整除、每、平均、倍”字眼，或特殊的数据“分数、百分数、比例”等。
三、特值法
在实际解题过程中，特值法能够帮助我们简化运算，提高解题速度。在解题时，有些未知量它的取值不固定，但无论取何值都不会影响最终的结果，这个时候我们可以把未知量设为方便计算的特殊值，这样就可以大大加快解题速度。
例题：手工制作一批元宵节花灯，甲、乙、丙三位师傅单独做，分别需要40小时、48小时、60小时完成。如果三位师傅共同制作4小时后，剩余任务由乙、丙一起完成，则乙在整个花灯制作过程中所投入的时间是（ ）。
A.24小时 B.25小时 C.26小时 D.28小时
【思路梳理】
工程问题一般围绕工作总量=工作效率×工作时间的关系解题。本题中，已知三人单独完成总工作量的工作时间，可以将设工作总量为各完工时间的公倍数，再得到三人的工作效率，进而求解题目。
【解析】
设工作总量为240（40、48、60的最小公倍数），则甲、乙、丙的工作效率分别为6、5、4。三位师傅共同制作4小时后，剩余任务由乙、丙一起完成，相当于整个工作甲只干了4小时，完成的工作量为4×6=24，剩余的工作量为240-24=216，都是由乙、丙合作完成，需要216÷（5+4）=24小时，即乙一共投入了24小时。故本题选A。
可以尝试将本道题中工作总量设为480或1，甚至设为x，但你会发现题目所求结果均为24小时。这就是未知量的取值不固定，但无论取何值都不影响结果。特值法的应用广泛，且在某些特定题型比如工程问题中，解题思路固定，很容易掌握。
四、比例法
比例法是方程法的一种“进阶”，其方法的应用也是对解方程过程的优化。通过分析题干中的比例关系，找到比例份数与实际量的对应关系，即一份是多少，再去求得问题所问，此为比例法的应用核心。而对于较为复杂的题目，往往先需要进行比例的统一，再用比例法解题。
例题：某单位原拥有中级及以上职称的职工占职工总数的62.5%。现又有2名职工评上中级职称，之后该单位拥有中级及以上职称的人数占总人数的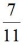
。则该单位原来有多少名职称在中级以下的职工（ ）？
A.68 B.66 C.62 D.60
【思路梳理】
题目中先后出现两个关于中级以上职称职工与职工总人数的比例，需要先进行比例的统一，再找到评上中级职称的2人所对应的比例份数，求出一份的数值，最后根据单位原中级以下职工的份数求出具体数值。解题时可以将题干出现的百分数转化成分数或比例，方便进行不同比例间的统一和对比，同时借助表格的形式更加有利于梳理题干中的比例关系。
【解析】
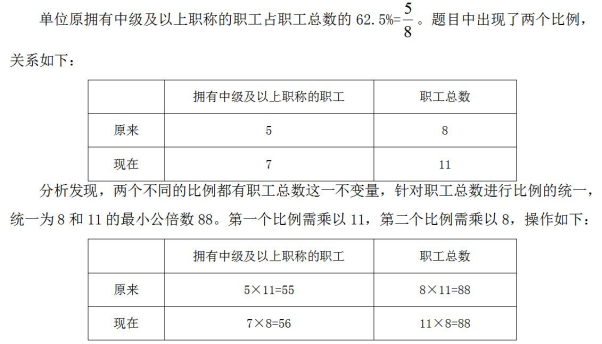
2名职工评上中级职称后，拥有中级及以上职称的职工增加了56-55=1份，即1份对应2人。而原来职称在中级以下的职工有88-55=33份，故对应66人。故本题选B。
五、十字交叉法
十字交叉的本质是盈亏思想，方法应用于比值混合问题。如，浓度混合、平均数混合、普通计算问题中的比值混合等都可以使用。在近些年的考试中经常会出现能够应用此种方法的题目。这种方法的优势在于简化解方程的计算过程，所以熟练掌握这种方法必然会节约考试中的解题时间。
（一）基础知识：
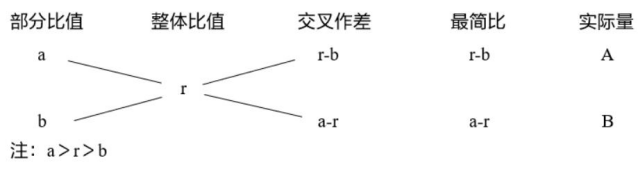
（二）计算关系：
1.三组基本计算关系：
①第一列和第二列交叉作差得到第三列（大数减小数）。
②第三列、第四列和第五列的比值相等。
③第一列的差等于第三列的和。
2.最简比（实际量之比）为部分比值的分母之比。
例题：甲、乙两队举行智力抢答赛，两队平均得分为92分，其中甲队平均得分88分，乙队平均得分94分，则甲、乙两队人数之和可能是（ ）。
A.20 B.21 C.23 D.25
【思路梳理】
平均分=总分÷总人数，即为比值。甲队平均分88和乙队平均分94混合成两队平均分92，即为比值的混合，满足十字交叉法应用环境。而计算平均分时，分母为人数，即为十字交叉模型中的实际量。
【解析】
已知甲、乙两队整体平均分，和甲、乙两队各自的平均分，根据十字交叉法可得：
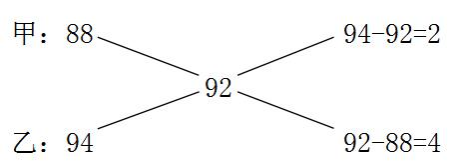
甲、乙两队平均分的分母之比即甲、乙两队人数之比为1∶2，两队人数之和为3份，可知人数和一定为3的倍数，符合的只有B选项。故本题选B。
【贴士】大家在学习过程中要掌握十字交叉法的应用环境和计算模型，在考试的时才能灵活应对解题。
以上便是学好行测数量关系的五大“秘籍”，也希望同学们可以在学习之后多加练习做到熟练应用，在考场更好地发挥。
