政华公考

【答案】C【解析】题干已知多个主体完工时间，可设工作总量为完工时间的公倍数，而为了计算得更加简便，一般设为最小公倍数。由题目已知，甲乙各自的完工时间，那么就设工作总量为10和15的最小公倍数，也就是30。通过公式：工作效率=工作总量÷工作时间，从而得到甲的效率是3，乙的效率是2。最终求合作所需时间，直接用工作总量÷合作工作效率和，即30÷（2+3）=6天，选C。

例2：甲、乙两队完成一项工程的效率比为2∶5。该项工程，若由甲工程队先单独做3天，再由乙工程队单独做4天，最后由甲、乙两个工程队合作6天刚好完成。问若由甲工程队单独完成，需要多少天（）？

A.30 B.32 C.34 D.36

【答案】C【解析】题目直接给了甲乙的效率之比，已知多个主体效率关系时，一般可将效率最简比设为各自的效率，也就是甲的效率是2，乙的效率是5。这道题最终求这项工程由甲工程队单独完成的时间，已知甲工程队的效率，还需知道这项工程的工作总量。梳理一下题干所给的工作方式。甲工程队单独做3天，再由乙工程队单独做4天，最后甲乙两个工程队合作6天刚好完成，所以工程的工作总量为：3×2+4×5+6×（2+5）=68，最终甲工程队单独做所需的时间为68÷2=34天，选C。

例3：有一批工人进行某项工程，每个人的工作效率相同。如果能再调来8个人，10天就能完成；如果能再调来3个人就要20天才能完成。现在只能再调来2个人，那么完成这项工程需要多少天（）？

A.20 B.22 C.25 D.30

【答案】C【解析】设每个人的效率为1，原来有x个工人，所求为t天，则有（x+8）×10=（x+3）×20=（x+2）×t，解得x=2，t=25，选择C。

用特值法搞定多者合作

公式

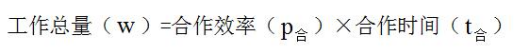
解题技巧

关于多者合作问题我们可以根据题干特征，将常考题型分为三类进行设特值解题。

题型一：设工作总量（W）为特值：题干中已知不同主体单独完成工程的时间，可设工作总量为已知完成工程时间的最小公倍数。

【例1】单独完成某工程，甲、乙、丙三人分别需要10小时、15小时、20小时，开始三人一起干，后因工作需要，甲中途调走了，结果共用了6小时完成了这项工作。那么，甲实际工作了（）小时。

A.2 B.4 C.5 D.3

【答案】D【解析】题目中给出甲、乙、丙三人完成时间分别为10小时、15小时、20小时，设工作总量为10、15、20的最小公倍数60，得到甲、乙、丙的工作效率分别为60÷10=6、60÷15=4、60÷20=3。根据“甲的工作量+乙的工作量+丙的工作量=工作总量”建立等量关系，可以设甲工作的时间为t小时，乙、丙未调走则工作时间均为6小时，可以得到6t+4×6+3×6=60，解方程得到t=3天，选择D项。

题型二：设工作效率（p）为特值：题干中已知工作效率的比值关系，可以设工作效率为已知工作效率比值的最简比。

【例2】一项工程，甲先单独做2天，然后与乙合作7天，这样才能完成工程的一半。已知甲、乙工作效率的比是2:3。如果这项工程由乙单独做，需要（）天才能完成。

A.22 B.23 C.24 D.26

【答案】D【解析】题目给出甲、乙的工作效率比是2:3，则设甲的工作效率为2，乙的工作效率为3，根据“甲的工作量+乙的工作量=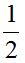工作总量”建立等量关系，已知甲先工作2天，和乙再工作7天，可得工作总量（W）=2×（2×2+2×7+3×7）=78，根据工作量一定，设乙单独完成需要t天，则3t=78，解方程得到t=26天，选择D项。

题型三：设工作效率（p）为特值：题干中已知多个效率相同的人或物共同完成一项工程，可设定单个人或物的工作效率为1。

【例3】某制衣厂有一批衣服要加工完成，假设每个工人每天的效率相同，则计划派180名工人工作12天即可完成。在工作4天后，由于特殊原因需要提前2天完成衣物的加工。问需要增加多少名工人（）？

A.40名 B.50名 C.60名 D.70名

【答案】C【解析】题目中给出多个效率相同的工人，可设每名工人的工作效率为1，180名工作的效率为180，根据工作总量一定，设需要增加n人，可以得到，180×12=180×4+（180+n）×（12-4-2），解方程得到n=60人，选择C项。

通过以上讲解，相信大家对于多者合作问题的三种常见设特值的题型有了一定的了解，大家可以通过做题巩固这类题目，相信熟能生巧以后能够对于我们数量关系得分有一定的帮助。

交替合作干活不累，找准循环效率更高

一、题型特征

背景多与工程问题相关，但工作方式却为多个主体按照一定规律交替轮流去做，如一项工作由甲先做1个小时，再交由乙做1个小时，再交由甲做1个小时，乙做1小时……如此下去，直到完成全部工作，这类问题称为交替合作问题。

二、解题步骤

（一）只有正效率的交替合作

1.确定工作总量和各自工作效率，一般通过特值法运算确定；

2.寻找循环规律，找出最小的循环周期并求出最小循环周期内的工作量；

3.确定完整周期数：周期数=工作总量÷一个周期工作量；

4.确定完整周期之外剩余工作量所用时间；

5.根据问题求解答案。

（二）含有负效率的交替合作

1.确定工作总量和各自工作效率，一般通过特值法运算确定；

2.寻找循环规律，确定每个循环周期中的效率峰值，峰值即为一个循环中的效率可达到的最大值；

3.找出最小的循环周期并求出最小循环周期内的工作量；

4.确定完整周期数：周期数=（工作总量-峰值）÷一个周期工作量；

5.分析完整周期以外的剩余工作量。

三、经典例题

【例1】完成一项工程，甲单独做需要18小时，乙需要24小时，丙需要30小时，现甲、乙、丙的顺序轮流工作1小时，当工程完工时，乙需要工作多少个小时（）？

A.8小时 B.7小时44分钟 C.7小时 D.6小时48分钟

【答案】B【解析】根据甲、乙、丙单独做需要18、24、30小时，可设工程量为360，那么甲的工作效率为360/18=20，乙的工作效率为360/24=15，丙的工作效率为360/30=12。而题干要求按甲、乙、丙的顺序轮流工作1小时，即甲干1小时，乙干1小时，丙干1小时，接下来再次循环直到完工，我们就可以把甲干1小时，乙干1小时，丙干1小时来当做一个循环来看，那么一个循环就可以完成20+15+12=47的工作量，360/47=7……31，即经过7个循环之后还剩下31的工程量没有完成，继续按照甲乙丙各一小时的顺序，甲1小时完成20，工程量剩下11，乙再工作11/15 60=44分钟即可完工，那么在整个过程中乙工作了7小时44分钟，故答案为B。

【例2】一个水池有甲乙两个进水管，一个丙出水管，单开甲管6小时注满，单开乙管5小时注满，单开丙管3小时放完。水池原来是空的，如果按甲乙丙的顺序轮流开放三个水管。每轮中各水管均放开1小时，那么经过多少小时后水池注满（）？

A.57 B.58 C.59 D.60

【答案】C【解析】依题意，甲、乙进水管注满一池水分别需要6小时和5小时，丙放完一池水需要3小时，设工作总量为30，那么甲、乙、丙的效率分别为5、6、-10。按照甲乙丙的顺序进行，那么周期峰值就是5+6=11，那么周期数为（30-11）÷（5+6-1）=19那么所需要的时间为19×3+1+1=59小时，故答案为C。

通过上面两道例题的讲解，相信大家应该对交替合作问题当中只有正效率和含有负效率的两种考查形式有所了解，希望大家接下来能够通过练习巩固并灵活运用交替合作问题的解题思路。