政华公考

【答案】B【解析】本题需对比找出运费最少方案，可依次对比选项。将煤集中于甲或乙，均需先将丙、丁处的煤运送到乙，此时甲有100吨，乙处有90+12=102吨，而集中于甲还需运送乙处102吨煤，集中于乙只需运送100吨煤，单价与距离相同，可得集中于乙运费更少。同理，集中于乙或丙，均需先将甲处煤运送于乙，此时乙、丙分别为190吨和12吨，运送12吨至乙比运送190吨至丙便宜。最后，若集中于丁，所有货物运送至丙后还需再运送3千米，运费贵于集中到丙。故最少运费方案为集中到乙，选择B。

小结：此类货物集中问题，对于相邻集中点，均需先将其他货物运送至这两点，只需对比此时两点货物总数进行对比，选择将货物更轻的一点向另一点运送即可。

【例2】有甲、乙、丙三个工作组，已知乙组2天的工作量与甲、丙共同工作1天的工作量相同。A工程如由甲、乙组共同工作3天，再由乙、丙组共同工作7天，正好完成。如果三组共同完成，需要整7天。B工程如丙组单独完成正好需要10天，问如由甲、乙组共同完成，需要多少天（）？

A.不到6天 B.6天 C.7天 D.7天多

【答案】D【解析】A工程可由甲乙合作3天加上乙丙合作7天完成，也可由甲乙丙合作7天完成，将甲乙丙每天工作量分别记为x、y、z，得3x+3y+7y+7z=7x+7y+7z，等式两边消去3x+7y+7z得3y=4x，即y∶x=4∶3，设乙组每天工作量为4份，甲为3份，根据“乙组2天的工作量与甲、丙共同工作1天的工作量相同”得丙每天工作量为4×2-3=5份，因此B工程总量为5×10=50份，由甲乙合作需50÷（3+4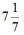）=天，故选择D选项。

小结：多者合作问题中，若同一工程按不同方案完成，可消去相同的部分，再分析方案间的差异，根据剩余工作量相等建立等量关系，进而得出工作效率关系或直接进行等量替换。

【例3】某单位志愿者团队在重阳节购买了一批牛奶，到“夕阳红”敬老院维稳孤寡老人，如果给每个老人分5盒，则剩下38盒；如果每个老人分6盒，则最后一个老人不足5盒，但至少分得1盒，问该敬老院至少有多少名老人（）？

A.39 B.40 C.41 D.42

【答案】B【解析】方法一：，设有x位老人，最后一位老人分得n盒（1≤n<5），根据牛奶总盒数不变可得5x+38=6（x-1）+n，化简得x=44-n，n取最大值4时x有最小值为44-4=40，故选择B。方法二：若要每个老人分够6盒，还差2至5盒，对比每人分够5盒的方式，每人多分一盒，需额外分38+2=40盒至38+5=43盒，故人数最少为40，选择B。

小结：多方案分配问题中，根据多种方案剩余量或缺少量的对比，结合每个主体分配量的差异可快速计算得到主体数量。

通过以上题目相信大家对差异对比的思维有了一定的认识，也能感受到它可以应用到很多题目中，希望大家多总结，多练习，提高解题速度。

化除为乘，将速算做到极致

行测作为公考笔试中非常重要的一门，其难点不在于题目本身有多难，而在于需要在限定的时间内把题目做完，所以如何“抢时间”成为众多考生备考路上的必修课。在资料分析中，要想节约时间，则需要进行快速地估算。下面给大家介绍一下在一步除法中非常实用的一种口算技巧——化除为乘。

一、知其然，知其所以然

化除为乘：运用平方差思想，把一步除法转化为乘法，进而简化运算。

通过以上两个式子可以看出，当遇到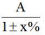列式类型时，可以近似转化成乘法进行运算，但是注意计算出的结果略偏小，需要选择相对偏大的选项。

注意：x%越大，计算的结果与实际值相差越大，一般建议：

0<x%<5%时，可以得到近似答案，可忽略放缩问题；

5%<x%<10%时，注意判断放缩；

x%>10%时，误差较大，一般不建议使用，但也可以结合选项综合考虑。

二、趁热打铁，方能如臂使指

例1：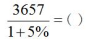

A.3242 B.3398 C.3483 D.3569

【答案】C【解析】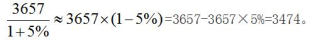计算结果偏小，选择偏大的C选项。

例2：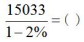

A.15112 B.15340 C.15546 D.15709

【答案】B【解析】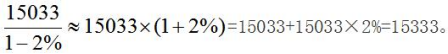选择最相近的B选项。

三、纸上谈兵，不如沙场点兵

2012年1-4月我国生产手机3.5亿部，增长4.7%；移动通信基站3903.7万信道，增长57.8%；固定电话程控交换机1105.0万线，下降29.9%。据统计1-4月全国电信业务总量累计完成4190.6亿元，比上年同期增长14.8%。移动通信收入累计完成2461.3亿元，比上年同期增长12.9%，在电信主营业务收入中所占的比重从上年同期的70.75%上升到72.59%；固定通信收入累计完成929.2亿元，比上年同期增长3.1%，在电信主营业务收入中所占的比重从上年同期的29.25%下降到27.41%。

问题：2011年1-4月全国固定通信收入累计完成多少亿元（）？

A.836 B.855 C.873 D.901

【答案】D【解析】由材料可知，2012年1-4月固定通信收入累计完成929.2亿元，比上年同期增长3.1%。故所求为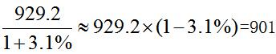，选择最近的D选项。

通过以上题目练习，希望大家以后在遇到题目是求基期值，且所给的增长率较小，可以考虑通过化除为乘的方法进行口算，快速勾选接近的答案，节约做题时间。

巧用比例速解题

在近几年行测数量关系考试中，能够利用比例关系解题的题目越来越多，使用比例能够更快速、更简单地直通答案。但是很多考生掌握不熟练，并不能在第一时间想到使用比例方法，只能按照传统方法列方程计算，费时费力。在此给大家分享一下，如何能够快速识别题目可以应用比例法以及如何应用比例法，助力大家快速解题。

比例即数量间的对比关系，就是用份数之比来代替两个相关联的实际量之比，以反映这两个关联量之间的关系。常见的比例应用有以下两种：

第一种为题干中给出比例关系，并给出与比例相关的实际值（注意此应用环境对应比例的简单计算和比例的统一），如例1。

【例1】甲单位的职工人数是乙单位的60%，是丙单位的1.5倍。现从乙单位调出4人到甲单位、调出X人到丙单位后，三个单位职工人数相同。X的值为：（）

A.12 B.16 C.20 D.24

【思路点拨】此题中虽然给出的占比关系，但是百分数和比例是可以互相转化，所以也可以理解为给了比例关系。

【答案】B【解析】甲单位的职工人数是乙单位的60%，则甲、乙单位的职工人数比为0.6：1=3：5，甲单位的职工人数是丙单位的1.5倍，则甲、丙单位的职工人数比为1.5：1=3：2，则甲、乙、丙三个单位的职工人数比为3：5：2。设甲、乙、丙三个单位的职工人数分别为3a、5a、2a。当三个单位职工人数相同时，每个单位的职工人数为（3a+5a+2a）/3=根据“乙单位调出4人到甲单位”可知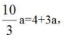，解得a=12，则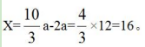故本题选B。

【注意】此题中比例关系找出来之后发现甲单位在两个比例中的份数是一致的，故可以将两个比例直接串联，若甲单位在两个比例中份数不一致，则需要统一比例的份数再建立联系。

整除法在行测计算问题中的妙用

行测数量关系中部分计算问题题干长，计算复杂，在考试时会耗费很长时间，今天带大家来学习整除法在计算问题中的妙用。

一、什么是整除

被除数、除数、商均为整数，且余数为零。我们就说a能被b整除（或说b能整除a）。

二、整除法应用的核心

利用整除特性排除错误选项。

三、应用环境

整除法在数学运算中应用环境一般分为两种：

①文字描述整除：题干有明显整除字眼、出现“每”“平均”“倍数”；

②数据体现整除：出现分数、百分数、比例等。

四、实战演练

【例1】小雪和小敏的藏书册数之比是7:5，如果小雪送65本给小敏，那么他们的藏书册数之比是3:4，则小敏原来的藏书是多少册？（）

A.175 B.245 C.420 D.180

【答案】A【解析】现在两人的藏书册数之比是3:4，即小敏原来的藏书册数加上65之后能被4整除，验证后只有A满足题意，选择A选项。

【例2】袋子里红球与白球的数量之比为19∶13，放入一定数量的红球之后，红球与白球的数量之比5∶1，又放入一定数量的白球后，红球与白球的数量之比为13∶11，此时袋中红球比白球多300个，问袋中最初有多少个球（）？

A.650 B.720 C.840 D.960

【答案】D【解析】最初红球与白球的数量之比为19∶13，即袋子里最初红球的个数一定是19的倍数，白球的个数一定是13的倍数，总球的个数一定是32的倍数。所以结果应该具备能够被32整除的整除特点，综合选项只有D选项满足题意，选择D选项。

【例3】两个派出所某月内共受理案件160起，其中甲派出所受理的案件中有17%是刑事案件，乙派出所受理的案件中有20%是刑事案件，问乙派出所在这个月中共受理多少起非刑事案件（）？

A.48 B.60 C.72 D.96

【答案】A【解析】已知甲派出所的刑事案件占17%=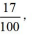。根据整除特性可知，甲派出所受理的案件总数是100的倍数，又因甲、乙两派出所共受理案件160起，故甲派出所受理案件总数只能是100，则乙派出所受理案件总数为60，在这个月中共受理的非刑事案件数为60×（1-20%）=48起，选择A选项。

希望大家可以通过对题干的分析来判断是否能够利用整除特性，进而结合选项，快速排除错误选项。