
行测技巧:掌握技巧轻 松解决行程问题
巧用正反比
在行测数量关系备考过程中,很多同学都直呼有难度、没思路,持有一种放弃的心态。其实不然,今天就要带大家学习除了用最基本的方程法解答行程类问题外,我们还可以用有时更为便捷的正反比解法。其题型明确,解法清晰,可适当减轻大家做这类题目的负担。
一、知识精讲
行程问题主要研究的就是路程、速度和时间之间的关系:路程=速度×时间。当路程、速度、时间三个量中有一个是固定不变的,我们就可以考虑正反比解法:
基本公式:路程=速度×时间
1、当路程一定时,速度与时间成反比;
2、当速度一定时,路程与时间成正比;
3、当时间一定时,路程与速度成正比。
二、经典例题
1、当路程一定时,速度与时间成反比:
【例1】邮递员骑自行车从邮局到渔村送邮件,平时需要1个小时。某天,在距离渔村2公里处,自行车出现故障,改成步行。已知步行速度为自行车车速的,结果比平时多用22.5分钟。问邮局到渔村的距离是多少公里( )?
A.15
B.16
C.18
D.20
【答案】B【解析】由题意可知,步行速度与自行车速度之比为1:4,故障地与渔村的距离一定,为2公里,那么速度与时间成反比,即步行时间与自行车时间之比为4:1,所以步行时间比自行车时间多用三份,其对应22.5分钟,即,即自行车骑行两公里的时间为7.5分钟,所以骑行1小时(60分钟)的距离为,即邮局到渔村的距离为16公里,故此题选B。
2、当速度一定时,路程与时间成正比:
【例2】一支军队共有20辆大拖车,每辆车身长20米,两辆车之间的距离是10米,行进的速度是54km/h。这支车队需要通过长760米的桥梁(从第一辆车头上桥到最后一辆车尾离开桥面计时),以双列队通过与以单列队通过花费的时间比是( )。
A.7:9
B.29:59
C.3:5
D.1:2
【答案】A【解析】在这道题当中,我们会发现无论是单列队还是双列队,它们的速度都是相同的,因此所求的时间与路程成正比。单列队时:车队长度为20×20+19×10=590米,过桥总路程为590+760=1350米。双列队时:车队长度为10×20+9×10=290,过桥总路程为290+760=1050米。因此时间之比等于路程之比,即1050:1350=7:9,故此题选A。
3、当时间一定时,路程与速度成正比:
【例3】甲、乙、丙三人同时从起点出发,匀速跑向100米外的终点,并在到达终点后立刻匀速返回起点。甲第一个到达终点时,乙和丙分别距离终点20米和36米。问当丙到达终点时,乙距离起点多少米( )?
A.60
B.64
C.75
D.80
【答案】C【解析】当甲第一个到达终点时,甲、乙、丙三个人分别跑了100米、80米、64米,所用时间相同,路程与速度成正比,所以甲、乙、丙三人速度比为100:80:64。当丙到达终点时,三人所用时间相同,路程与速度成正比,可得当丙跑100米时,可解得乙跑了125米,此时距离起点100-25=75米。故此题选C。
通过以上题目的总结发现,解决行程类问题,我们只需要找到三个量中的不变量,再根据另外两个量中的已知量之间的比值,推知另一个量的比值关系,找到实际值与比例的对应关系,进而根据题干要求寻找到答案。
比例法
学习比例法首先需要掌握比例的性质。一般而言我们使用最多的是比例的基本性质:路程=速度×时间,速度一定则路程与时间成正比;时间一定则路程与速度成正比;路程一定则速度和时间成反比。基本性质很简单,但在实际应用中还需要灵活应变。
下面我们来看几道题:
【例1】小王每天以v千米/小时的速度骑车到单位上班,如果速度提高20%,则可以提前10分钟到单位;如果以原速度骑行2千米后再提速30%,也可以提前10分钟到达。问小王家距离单位多少千米( )?
A.5.4
B.7.2
C.8.5
D.9.6
【答案】B【解析】第一步,本题考查行程问题,用比例法解题。
第二步,提速20%,则提速前和提速后的速度比为5∶6,那么提速前和提速后的时间比为6∶5,根据提前10分钟到达可知时间比例中的一份为10,则以v千米/小时的速度行驶到单位用的时间为6×10=60分钟=1小时,当以原速度行驶2千米再提速30%,提速前和提速后的速度比为10∶13,那么提速前和提速后的时间比为13∶10,根据提前10分钟到达可知时间比例中的3份为10,一份为10/3 ,则行驶2千米后以原来速度行驶需要的时间为13×(10/3) = 130/3,那么以原速度行驶2千米的时间为60- (130/3)=50/3 分= 5/18小时,原速度v=2÷(5/18) = 36/5千米/小时,小王家距离单位的路程为36/5 ×1=7.2千米。因此,选择B选项。
【例2】早上8:00,甲、乙两车开始在A、B两地之间往返运货,两车先在A地装货后驶往B地卸货,然后返回A地再装货,如是重复。13:35甲完成了第四次卸货,又过了2小时5分,乙完成了第五次装货。已知两车均匀速行驶,每次装货或卸货需要20分钟,则甲的行驶速度是乙的多少倍( )?
A.1.25
B.1.4
C.1.5
D.1.6
【答案】B【解析】第一步,本题考查行程问题中的基本行程类。
第二步,分别设甲、乙两车从A地到B地路上的时间为x、y,根据题意,甲车从8:00到13:35甲完成了第四次卸货,一共经历了8次装卸货和7次路途。列式为:8×20+7x=5小时35分=335分钟,解得x=25(分钟)。乙完成了第五次装货,乙车在第四次卸货之后多了1次装货和1次路途。列式为:9×20+8y=335+125,解得y=35(分钟)。
第三步,由于路程相同,速度与时间成反比,甲的速度∶乙的速度=y∶x=35∶25=7∶5=1.4,那么甲的速度是乙的1.4倍。因此,选项B选项。
行程图
1、梳理题干运动过程
大家做行程问题的难点在于难以理解题干运动过程,而行程图可以帮助我们理清题干的运动过程。
【例1】甲从某地出发匀速前进,一段时间后,乙从同一地点以同样的速度同向前进,在K时刻乙距起点30米;他们继续前进,当乙走到甲在K时刻的位置时,甲离起点108米。求乙所走过的路程。
【解析】根据题意可画出下图,在K时刻,甲和乙分别在A、B两点,且相隔距离表示为a米,他们继续前进,乙从B点前进到A点,同时甲从A点前进到C点,因为两人以相同的速度匀速前进,所以A、C两点之间的距离也为a米。

这样我们使用行程图就使题干运动过程直观地展现在我们眼前,从而会使后续解题过程变得简单。
通过寻找行程图上线段间的等量关系,可达到最终的解题目的。如上题,根据图中线段间的关系可得30+a+a=108,解得a=39,故整个过程中乙走了30+39=69米。
2、构造等量关系
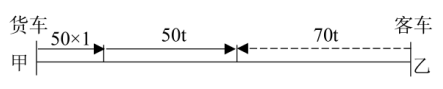
【例1】甲乙两座城市相距530千米,货车和客车分别从两城出发,相向而行。货车每小时行50千米,客车每小时行70千米。客车因故比货车晚出发1小时,两车在途中某地相遇。问相遇时货车行驶多少千米( )?
A.100千米
B.150千米
C.200千米
D.250千米
【答案】D【解析】设客车出发后,经过t小时两车相遇,作图如下,则有50+50t+70t=530,解得t=4,故相遇时货车行驶了50+50×4=250千米。
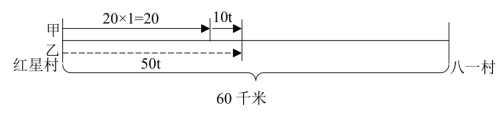
【例2】某宣讲团甲宣传员骑摩托车从红星村出发以20千米/时的速度去相距60千米的八一村,1小时后由于路面湿滑,速度减少一半,在甲出发1小时后,乙宣传员以50千米/时的速度开车从红星村出发追甲,当乙追上甲时,他们与八一村的距离为( )
A.35千米
B.30千米
C.25千米
D.40千米
【答案】A【解析】设乙从出发到追上甲所用的时间为t小时,结合题意作图如下,根据图中线段间的关系可得,20+10t=50t,解得t=0.5,所求为60-50t=35千米。
通过上面的例题,大家会发现行程图一方面帮助我们理清了运动过程,另一方面帮助我们找到了等量关系以达到最终解题的目的,可谓一举两得。








