行测数量关系：特值法解决工程问题
数量关系作为行测考试的“种子”题型，让很多考生望而却步，实际上随着报考人数的增加，数量关系的重要性也在不断上升，作为区分度较高的考察部分，不建议考生全部放弃，实际上数量关系并不全部都是难题，还是有一半以上都是基础题型，我们可以采用选做的策略来选择自己熟悉或者较为简单的题型来做。当然，今天要给各位考生介绍的便是其中不需要过多逻辑上思考的一类题型：工程问题，针对这类题型我们也会介绍适用于其的解题技巧，特值法，接下来带大家一起来学习一下。
一、工程问题
概念：工程问题是研究工作效率，工作时间，工作量之间关系的应用题。
求解工程问题重点要掌握相关公式，并把控不同工作方式当中的不变量，通过不变量或基本公式来建立等量关系来求解。主要公式如下：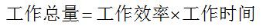
。
如果用W来表示工作总量，P来表示工作效率，t来表示工作时间，也可表示为：
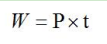
将公式进行变形也可得到工作效率和工作时间的式子：
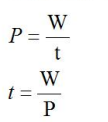
二、工程问题之特值法
特值法的本质仍旧是方程，只不过在实际运算过程中通过特值题干中的某些未知量为特殊值，再结合工程问题的基础公式，从而简化运算，快速求得答案的思想。特值法在工程问题中的使用有以下三种常见题型：
当题干中给出多个完工时间，可以将工作总量设为完工时间的公倍数（常为最小公倍数）或者1。
【例1】有一项工作，甲单干需要10个小时完成，乙单干需要12个小时完成。甲、乙两人同时工作5小时后，甲离开，只有乙继续工作，则完成这项工作共用了（ ）小时？
A.5 B.6 C.7 D.8
【答案】B【解析】题干给出甲、乙单独完成工作的时间分别为10小时和12小时，所以可以特值总工作量为60（10和12的最小公倍数）。根据工程问题基本公式，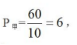
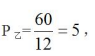甲、乙合作5小时后剩余工作量60-（6+5）×5=5，乙还需工作
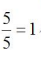小时，所以完成这项工作共用5+1=6小时，选择B选项。
当题干中给出多个合作对象的效率比值，可以直接将效率比设为效率值。
【例2】某车间有甲、乙、丙三人，其工作效率比为3：4：5。甲单独加工A类产品需要50小时，丙单独加工B类产品需要18小时。现由甲负责加工B类产品，乙负责加工A类产品，丙先帮助甲加工B类产品若干天后转去帮助乙加工A类产品。如要求加工A、B两类产品，且同时开工、同时完工，则丙帮甲工作的时间与丙帮乙工作的时间之比为（ ）？
A.7：3 B.3:7 C.5:3 D.3:5
【答案】B【解析】根据题干描述，给出了甲乙丙三人的效率比值，可以运用特值法直接设甲、乙、丙的工作效率分别为3、4、5，根据工程问题基本公式，A类产品的工作量为3×50=150，B类产品的工作量为5×18=90。设丙帮甲、乙工作的时间分别为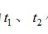
小时。可得
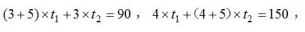解得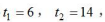
故丙帮甲工作的时间与丙帮乙工作的时间之比为6:14=3:7。选择B选项。
当给出多个工作对象效率相同时，可以将每个工作对象单位时间工作效率特值为1。
【例3】有20名工人修筑一段公路，计划15天完成。动工3天后抽出5人去其他工地，其余人继续修路。如果每人工作效率不变，那么修完这段公路实际用（ ）。
A.19天 B.18天 C.17天 D.16天
【答案】A【解析】本题当中没有明确给出每名工人的工作效率，但题干明确指出“每人工作效率不变”，默认都相同，此时可以用特值法设每人的工作效率为1，根据工程问题基本公式，动工3天后余下的工作量为20×1×（15-3）=240，需要用240÷（20-5）=16天，则修完这段公路实际用3+16=19天。选择A选项。
已知多个主体的完工时间，设工作总量为“1”或为多个完工时间的最小公倍数。
某项工程，甲施工队单独干需要30天才能完成，乙施工队需要40天才能完成。甲、乙合作干了10天，因故停工10天，再开工时甲、乙、丙三个施工队一起工作，再干4天就可全部完工。那么，丙队单独干需要大约（ ）天才能完成这项工程。
A.21 B.22 C.23 D.24
【答案】B【解析】
方法二，设该工程总量为120（30和40的最小公倍数），则甲、乙的工作效率分别为4、3。前10天甲、乙共做了10×（4+3）=70，剩余工作量为120-70=50，甲、乙、丙合作的工作效率之和为50÷4=12.5，则丙的工作效率为12.5-7=5.5，丙单独完成该项工程，需要120÷5.5≈22天。故本题选B。
根据例题的两种解法我们可以发现，当题干中给多个主体的独立完工时间时，两种方法都需要通过设特值的工作总量求解出工作效率，进而求解最终的问题，但在第一种解法中，所求出的工作效率为分数，计算时还需要进行通分，较为麻烦，并且容易出错，而第二种方法中，可以效率几乎是整数，计算时更简洁，因此，在题干中给多个主体的独立完工时间时，推荐大家设工作总量为多个完工时间的最小公倍数。
已知多个主体的效率比，将效率特值为最简比的数值。
甲、乙、丙三个工程队的效率比为6∶5∶4，现将A、B两项工作量相同的工程交给这三个工程队，甲队负责A工程，乙队负责B工程，丙队参与A工程若干天后转而参与B工程。两项工程同时开工，耗时16天同时结束。问丙队在A工程中参与施工多少天（ ）？
A.6 B.7 C.8 D.9
【答案】A【解析】设甲、乙、丙三个工程队的效率分别为6、5、4，故工作总量为（6+5+4）×16=240，A工程的工作量为240÷2=120。则有120=6×16+4×t，解得t=6天。故本题选A。
通过上面的题，大家也可以发现，虽然工程问题的题干看起来比较复杂，但考查内容非常固定，就是工作总量、工作效率、工作时间三者之间的关系，只要大家在做题时，明确题干所求和所给量，用对应的解题方法求解即可。
