政华教育

【答案】A【解析】题干描述了两种不同方式完成同一个工程，故可以通过工作总量相等建立等量关系，由于时间未知，我们可以假设原计划时间为t，第一种方式的工作总量表示为200t+1000，第二种方式为250t-200，200t+1000=250t-200，解得t=24天，代入第一种方式中总量200×24+1000=5800米。故本题选A。

二、多者合作问题

解题策略：梳理题干描述的不同合作方式，合理利用特值，再进行求解。

例2.一项工程，甲乙合作完成需要42天，乙丙合作完成需要30天，甲丙合作完成需要35天。现安排三人合作17天，然后由甲丙合作完成剩余工作，最后根据三人实际完成的工作量支付报酬。问丙获得的报酬约为乙的多少倍（）？

A.1.7 B.1.9 C.2.1 D.2.3

【答案】C【解析】根据题意，设工作总量为42、30、35的最小公倍数210，则甲乙的工作效率之和为210÷42=5，乙丙的工作效率之和为210÷30=7，甲丙的工作效率之和为210÷35=6，则甲的效率为2，乙的效率为3，丙的效率为4。结合题目条件，三人合作17天，完成的工作量为（2+3+4）×17=153，剩余工作量为210-153=57，还需要57÷6=9.5天可以完成。乙实际完成的工作量为17×3=51，丙实际完成的工作量为（17+9.5）×4=106，则所求为106÷51≈2.1倍。故本题选C。

小妙招：题干给出多个主体的完工时间，将多个主体完工时间的最小公倍数设为工作总量，再进行求解。

例3.甲、乙两人工作效率之比为3∶4。一项工作，甲单独做需要120天刚好完成。现安排两人合作，按照甲单独工作2天、乙单独工作2天、甲单独工作1天、乙单独工作1天……的顺序交替工作，直至完成工作。问，乙一共工作了多少天（）？（不足一天按一天算）

A.50 B.51 C.52 D.53

【答案】B【解析】根据题意，设甲、乙两人的工作效率分别为3和4，则工作总量为3×120=360。实际工作中，每2+2+1+1=6天一个周期，每个周期完成的工作量为3×2+4×2+3+4=21，360÷21=17……3，说明17个周期之后还剩下3的工作量，接下来轮到甲工作，刚好用1天完成剩余工作。则所求为17×（2+1）=51天。故本题选B。

小妙招：题干直接给出效率比，根据效率比设效率为未知数或特值，再进行求解。

相信通过上面题目，大家已经学会了工程问题的具体方法，希望大家勤加练习，在考试中轻松解决工程问题。

特值思想

行测考试中，很多人总觉得数量关系很难，但其实这部分中也有比较简单的题目。今天就给大家介绍数量关系中的一个高频，并且比较容易得分的知识点——工程问题。其解题方式多种多样，特值思想就是其中的一种。只需理清楚题目本质，相信你也可以利用特值轻松解题。

一、基本公式

基本公式：工作总量（W）=工作效率（p）×工作时间（t）。

解题方法：特值法

二、例题展示

例1.一项工程，由甲、乙两个队合作10天可以完成，甲、丙两队合作15天可以完成，三队合作8天可以完成。则乙和丙合作的效率是甲单独做效率的多少倍（）？

A.2 B.1.5 C.1 D.3

【答案】A【解析】已知三种不同合作方式的完工时间，所以可将总量设为(10、15、8的最小公倍数)120，P甲+P乙=120÷10=12①，同理，P甲+P丙=8②，P甲+P乙+P丙=15③，联立解得P甲=5，P乙=7，P丙=3，则(P乙+P丙)÷P甲=(7+3)÷5=2，选择A项。

小结：当已知多个完工时间时，可将工作总量特值为完工时间的公倍数，进而将效率表示出来，再根据题意求解。

例2.某医疗器械公司为完成一批口罩订单生产任务，先期投产了A和B两条生产线，A和B的工作效率之比是2∶3，计划8天可完成订单生产任务。两天后公司又投产了生产线C，A和C的工作效率之比为2∶1。问：该批口罩订单任务将提前几天完成（）？

A.1 B.2 C.3 D.4

【答案】A【解析】由题意可得，A、B、C的工作效率之比为2∶3∶1。则设A的工作效率为2，则B的工作效率为3，C的工作效率为1，生产任务总量为（2+3）×8=40。根据“两天后公司又投产了生产线C”，可知A和B合作生产两天，剩余任务量由A、B、C共同完成。设A、B、C的合作时间为t天，可得（2+3）×2+（2+3+1）×t=40，解得t=5，则完成全部任务共用2+5=7天，则该批口罩订单任务将提前8-7=1天完成，选择A项。

小结：在多者合作问题中，当题干中直接或者间接给出最简效率比，则可以将工作效率特值为最简比数值，再根据题意求解。

例3.某农场有36台收割机，要收割完所有的麦子需要14天时间，现收割了7天后增加4台收割机，并通过技术改造使每台机器的效率提升5%。问收割完所有的麦子还需要几天（）？

A.3 B.4 C.5 D.6

【答案】D【解析】已知多台相率相同的机器合作完工，可设原来每台收割机的效率是“1”，则改造后的效率为1.05。设还需t天完工，根据前后工作总量不变得36×14=36×7+（36+4）×1.05t，解得t=6，所以还需要6天，选择D项。

小结：当题目中已知多个效率相同的元素（人/机器），可以将每个元素单位时间的工作量特值为“1”，进而求总量，再根据题意求其它。

以上便是工程问题中利用特值解题的常见形式，值得注意的是，在利用特值解题的同时，核心还是需要梳理出对应的合作完成方式，便可以快速求解。

比例法

工程问题是行测数量关系中较为常见的一种题型，通常我们会借助工作总量相等去构建等量关系进行求解，在做题的过程中我们也会通过赋值法求解，但是各位小伙伴有时也会发现单纯地使用方程法和赋值法解题也较为复杂，今天就带大家来学习一下比例法在工程问题中的应用。

首先，我们一起了解一下比例法在工程问题中的基本应用：

根据工程问题的基本公式W=P×T可知这三个量的比例关系：

1.当工作总量W一定时，工作效率P与工作时间T成反比；

2.当工作效率P一定时，工作总量W与工作时间T成正比；

3.当工作时间T一定时，工作总量W与工作效率P成正比。

其次，我们还需要明确比例法可使用的情况：

（1）存在不变量；

（2）题干中存在或可以得到比例关系；

两个条件同时满足的时候就可以使用比例法了。结合实际的应用，一般题干中涉及的工作总量不变，给出的工作效率的比例关系或者出现了工作效率的比例变化时，可根据效率和时间成反比得到时间的比例关系，然后进行求解（亦或者是得到时间比例关系，从而得到效率的比值）。

最后，进行一下实战演练：

例1.为响应建设“绿色城市”的号召，某社区党员义务植树300棵，由于参加植树的全体党员植树的积极性高涨，实际工作效率提高为原来的1.2倍，结果提前20分钟完成任务，则原来每小时植树多少棵（）？

A.120 B.150 C.135 D.125

【答案】B【解析】题目中总量保持不变且出现了工作效率的比值变化，则我们可以考虑用比例法求解。根据实际的工作效率为原来的1.2倍，可以得出——原来效率：实际效率=1：1.2=5：6；根据工作总量不变，效率和时间成反比可得——原来时间：实际时间=6：5，该比例代表着原来用6份时间，后来只需要用5份时间，少的1份时间既是对应题干中的“提前20分钟”，即1份=20分钟；则原来时间为：6份×20分钟/份=120分钟=2小时；由P=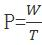，可得原来的效率为300÷2=150。故本题选B。

例2.某印刷厂原计划用全自动装订机花费4小时装订一批文件，但在还剩300份文件时装订机出现故障，无法装订。印刷厂立即安排了部分员工进行人工装订，由于人工装订的总效率仅为机器的20%，最终比原计划推迟1小时完成装订，则这批文件共有（）份。

A.2400 B.3600 C.4800 D.6000

【答案】C【解析】对于剩余的300份文件，由于从机器装订变为人工装订，而导致了时间推迟——此过程中，总量不变，且存在工作效率的比例变化，故可以用比例法。对于最后的300份文件而言，根据条件“由于人工装订的总效率仅为机器的20%”可以得到——机器效率：人工效率=1∶0.2=5：1；则根据“完成相同工作量所需时间之比是效率的反比”可以得到——机器完成时间：人工完成时间=1：5，在该时间比例中，两时间差4份，4份对应“推迟的1小时”，即4份=1小时，机器完成的时间需要1份时间，也就是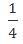小时；也就是说机器完成300份文件需要小时，则机器效率为：300÷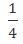=1200。再结合条件“机器全自动装订需要4小时完成”，可得这批文件共有1200×4=4800份。故本题选C。

通过以上两题的演练可见，比例法解决工程问题还是比较快捷的，各位小伙伴可以多练习几次，熟练掌握，这样才能够在较短的时间内拿到尽可能多的分数。

行测数量关系工程问题中的交替合作

在行测考试中，数量关系是让众多考生头痛不已的内容，数量部分涉及内容广泛，计算逻辑多变，是大家拉开分数差距的一部分内容。其实数量关系并不是所有的题目都晦涩难懂，能从中选出自己擅长的亦或是易于掌握的题型才是重中之重，像工程问题中的交替合作就是容易掌握的一类题型，接下来我们就一起来探索如何解决交替合作问题吧。

一、题型概述

交替合作即多个主体合作完成某项工程，合作过程中按一定规律进行轮流工作。

二、解题步骤

1.确定工作总量和各自的工作效率。若题目没有直接给出工作总量，通常用特值法（将工作总量赋值为多个主体完工时间的公倍数）；

2.找到最小循环周期，并求出一个周期内的工作量之和；

3.求出周期数，并确定整周期之外剩余工作量所用时间；

4.根据实际问题求解。

例1.一条隧道，甲单独挖要20天完成，乙单独挖要10天完成。如果甲先挖1天，然后乙接替甲挖1天，再由甲接替乙挖1天……两人如此交替工作。那么，挖完这条隧道共用多少天（）？

A.14 B.16 C.15 D.13

【答案】A【解析】设工作总量为甲、乙单独完工时间20和10的最小公倍数20，则甲的效率为20÷20=1，乙的效率为20÷10=2。将2天视为一个周期，则每个周期的效率为1+2=3，20÷3=6……2，说明经过6个周期后，剩余工作量为2，接下来甲再工作1天，乙再工作半天即可完成全部剩余工作，总的工作时间为6×2+1+0.5=13.5天，结合选项来看，挖完这条隧道共用14天，故本题选择A项。

例2.加工一批零件，甲单独工作需要80小时，乙单独工作需要120小时，甲乙丙三人合作需要50小时。每个人单独工作时的效率要比与别人合作时高25%。现在按照第一天甲乙合作，第二天甲丙合作，第三天乙丙合作的顺序轮班工作，每天工作8小时。当全部零件完成时，甲工作了多少小时（）？

A.50.4 B.48 C.26.4 D.24

【答案】A【解析】根据题意，设工作总量为80、120、50的最小公倍数1200，则甲单独工作的效率为1200÷80=15，与别人合作时的工作效率为15÷（1+25%）=12；乙单独工作的效率为1200÷120=10，与别人合作时的工作效率为10÷（1+25%）=8；三人合作时的工作效率之和为1200÷50=24，则丙与别人合作时的工作效率为24-12-8=4。甲乙合作的效率之和为12+8=20，甲丙合作的效率之和为12+4=16，乙丙合作的效率之和为8+4=12。按照题干要求，工作以3天为周期，前3天的工作总量为20×8+16×8+12×8=384，1200÷384=3……48，说明3个周期后，还剩下48的工作量，接下来轮到甲乙合作，还需要48÷20=2.4小时能够完成。甲在每个周期内的工作时间为8+8=16小时，则所求为16×3+2.4=50.4小时，故本题选A。

经过以上题目的学习，大家会发现这类题型其实并不难，是有一定规律的，但需要大家多加练习，熟练掌握，才能更好地灵活应用。