行测数量关系：巧解排列组合题
利用3个方法解排列组合
在行测考试中，数量关系是大多数考生的痛点也是难点，特别是排列组合问题更是让大家望而却步。但是对于这类题目，只要大家掌握一定的解题方法，问题就可以迎刃而解了。下面给大家介绍排列组合问题中常用的三个小方法。
一、优限法
有特殊元素或特殊位置的排列问题，通常是先安排特殊元素或特殊位置，即优先处理特殊元素（或位置）法，简称优限法。
【例1】学校准备从5名同学中安排3人分别担任亚运会3个不同项目比赛的志愿者，其中张某不能担任射击比赛的志愿者，则不同的安排方法共有（ ） 。
A.60种
B.24种
C.48种
D.36种
【答案】C【解析】共有三个项目，射击项目比赛对志愿者有限制要求，其他两类比赛没有，元素有限制要求用优限法。故优先选择射击运动志愿者，共有除小张4种选择，其他两个项目无要求有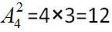
种选择，故不同的安排方法有4×12=48种。故选C。
二、捆绑法
解决元素相邻问题。元素要求相邻时，把相邻元素捆绑起来视为一个整体，再与其他元素进行排列，注意相邻的元素之间是否有顺序要求。
【例2】现在有五名男生和三名女生站成一排。若三名女生必须站在一起，则共有多少种不同的站法（ ）？
A.3440
B.3820
C.4410
D.4320
【答案】D【解析】这个题目当中我们看到题目要求三名女生必须站在一起，那其实就是说三名女生必须相邻。看到元素要求相邻的话呢，我们就要马上想到要去用捆绑法。因此我们在做题的时候直接把这三个女生绑在一起，把她们看成一个整体。
再与五个男生去进行任意排列，方法数有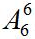
种。其次看内部需不需要顺序。女生的不同的站位会影响到最终的结果，所以说是需要顺序的，共有
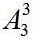方法。所以这道题一共有
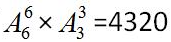种。选D。
三、插空法
解决元素不相邻问题。有元素要求不相邻时，先处理除不相邻元素以外的部分，再找出能够插入的空位，将不相邻的元素插入到不同的空位中。
【例3】某学习平台的学习内容由观看视频、阅读文章、收藏分享、论坛交流、考试答题五个部分组成。某学员要先后学完这五个部分，若观看视频和阅读文章不能连续进行，则该学员学习顺序的选择有（ ）种。
A.24
B.72
C.96
D.120
【答案】B【解析】根据题目中“观看视频和阅读文章不能连续”可知，此题可用插空法。
第一步，先排列除观看视频和阅读文章之外的三个元素，有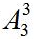
种方法。
第二步，三个元素排列后可产生4个“空”，将“观看视频和阅读文章”插入其中两个“空”，有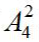
种，分步相乘，共有
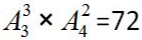种，故本题选B。
行测排列组合之“相邻对捆绑”
排列组合问题属于行测数量关系中的高频考点，也是学习过程中的难点、痛点。想要真正做对排列组合问题，除了需要掌握基础的分类分步思想和排列组合计算方法以外，还要掌握一些简便的做题技巧，今天就和大家来学习在排列组合问题中，可以解决元素要求相邻排序的方法——捆绑法。
一、题目特征
题目中遇到有元素要求相邻时使用。
二、解题原则
解题时应把相邻元素捆绑起来视为一个整体，与其他元素进行排列组合，并要考虑捆绑在一起的元素之间是否有顺序要求。
【例】将甲、乙、两种不同品牌的共享单车摆成一排，其中有3辆颜色不同的甲品牌共享单车，2辆颜色不同的乙品牌共享单车。乙品牌共享单车必须放在一起，那么一共有多少种不同的摆放情况？
题型分析：题干要求甲、乙品牌共享单车摆放共有多少种情况，是一道排列组合问题，并且需要满足乙品牌共享单车相邻这个条件，那么可以利用今天要学习的方法捆绑法来解决。
解题方法：首先把需要相邻元素2辆颜色不同的乙品牌共享单车捆绑将其视为一个整体，其次与其他没有要求的3辆甲品牌共享单车排列，有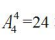
种排法，然后捆绑的元素内部可以互换顺序，有
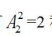种排法，最后结果表示为24×2=48种。
练一练：
【例1】某单位元旦晚会由2个独唱、2个舞蹈、1个诗朗诵、3个小品组成。在晚会上2个舞蹈节目要连续表演。问，一共有多少种不同的节目安排（ ）？
A.小于1000
B.1000~5000
C.5001~20000
D.大于20000
【答案】C【解析】题干要求2个舞蹈节目要连续，可利用捆绑法，首先将2个舞蹈节目看成一个整体，再跟其他节目进行排序，有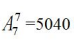
种，其次考虑2个舞蹈节目的顺序，有
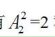种，则不同节目安排种数为5040×2=10080种，故本题选C。
【例2】某科室组织科室内8名员工看电影，其中包含2对夫妻。为保证观影效果，购票人员特意挑选了5排11-14号座位和6排11-14号座位。为了保证每对夫妻2人都相邻并且这2对夫妻不坐在同一排，一共有多少种不同的座次安排（ ）？
A.1728种
B.2126种
C.2248种
D.2400种
【答案】A【解析】将这2对夫妻分别安排在5排和6排，有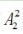
种不同的安排；接下来从剩下的4人中选择2人安排在5排与第1对夫妻就座，共有
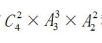种不同的安排；最后安排剩余的2人与第2对夫妻在6排就座，有
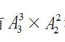种不同的安排，则所求为
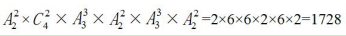种不同的座次安排。故本题选A。
利用捆绑法做题，大家首先要根据元素相邻的要求判断题型，明确可以利用“捆绑法”去解题，然后重点掌握“捆绑法”的做题步骤，并要注意捆绑内部的元素排列是否有顺序要求，希望大家在后续的学习过程中多加练习，真正掌握技巧方法。
排列组合问题之隔板法
一、隔板法的题型特征
一组相同的元素分成若干组（份），每组（份）至少分一个。
不难发现，隔板法的使用环境为分组，其特征为①相同元素，②每组至少1个，在考试中，我们就可以通过这两个特征来判断题型，从而快速锁定计算公式。
二、隔板法的计算公式
先确定空隙个数，为元素个数减1（n-1），再在空隙中插入隔板，此时隔板数为组数减1（m-1），则隔板法的计算公式为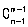
。
习题演练
【例1】把6本相同的书放进4个不同的抽屉，每个抽屉至少放1本书，则有几种放法？（ ）
A.4
B.6
C.10
D.24
【答案】C【解析】同元素即6本相同的书，即n=6，放进4个不同抽屉里，即将书分成4堆，m=4，代入隔板法公式有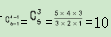
种不同的放法。故本题答案为C项。
【例2】某单位订阅了30份学习材料，准备发放给3个部分，每个部门至少发9份材料，共有多少种不同的发放方法？（ ）
A.7
B.8
C.12
D.10
【答案】D【解析】先给每个部门发放8份学习材料，还剩30-3×8=6份学习材料，此时每个部门至少还需发1份学习材料，符合隔板法使用条件，故共有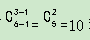
种发放方法。故本题答案为D项。
总结：隔板法是职测排列组合中容易判断出题型的题，需要同学们熟练掌握，在考场上一举拿下！
