行测备考技巧干货：概率问题的解题方法和技巧
在行测考试中，概率问题在近几年考试中每年都有出现，属于数量关系中的高频考点。
各位同学在备考过程中，可以对概率做一个专项练习，有目的地对概率问题做一个梳理，熟悉相关知识点，进而应用到解题过程中。
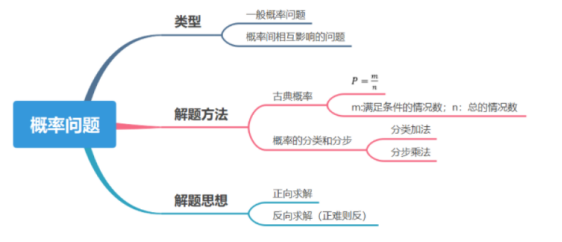
在大家通常所遇到的概率题中，有一般概率题和概率间相互影响的题，解题的过程中，大家可以选择用古典概率或者概率的分类分步解题。
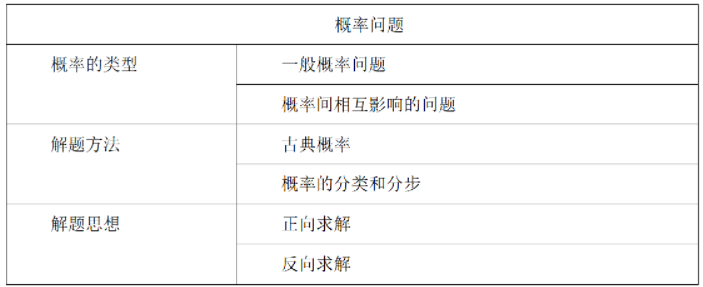
接下来通过表格的形式带领大家整理概率的知识点，通过例题向大家展示概率问题具体的解题过程。
【例1】某企业选拔170多名优秀人才平均分配为7组参加培训。在选拔出的人才中，党员人数比非党员多3倍。接受培训的党员中的10%在培训结束后被随机派往甲单位等12个基层单位进一步锻炼。已知每个基层单位至少分配1人，问甲单位分配人数多于1的概率在以下哪个范围内（ ）?
A.不到14%
B.14%～17%之间
C.17%～20%之间
D.超过20%
【答案】B【解析】第一步，本题考查概率问题，与约数倍数问题杂糅。
第二步，170多人，即总人数在170—179之间，可以被平分为7组，这范围内7的倍数只有175，那么这批人才共175人。党员比非党员多3倍，那么非党员如果为x党员人数为4x(注意不是3x)，5x=175，解得x=35，党员人数为35×4=140，进一步锻炼的人数为140×10%=14。
第三步，由于是14个人分到12个地方，人不一样需要考虑分配顺序，讨论如下：
每个地方至少分一个，分法有两种：①一个单位3人，其余单位1人，情况数为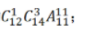
②两个单位2人，其余单位1人，情况数为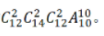
甲单位人数多于1也有两种情况：
①甲单位3人，情况数为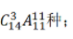
②甲单位2人，情况数为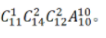
则满足题意的概率为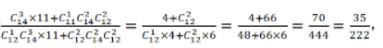
直除首两位商15,在14%~17%之间。
因此，选择B选项。
【例2】销售员小刘为客户准备了A、B、C三个方案。已知客户接受方案A的概率为40%。如果接受方案A，则接受方案B的概率为60%，反之为30%。客户如果A或B方案都不接受，则接受C方案的概率为90%，反之为10%，问将3个方案按照客户接受概率从高到低排列，以下正确的是：（ ）
A.A>B>C
B.A>C>B
C.B>C>A
D.C>B>A
【答案】D【解析】第一步，本题考查概率问题。
第二步，由题意可知接受A且接受B的概率为40%×60%=24%，不接受A但接受B的概率是60%×30%=18%，那么接受B方案的概率为24%+18%=42%。
第三步，如果A不接受，那么B不接受的概率就是70%，那么都不接受的概率是60%×70%=42%，这种情况下接受C的概率是90%，可知AB不接受但接受C的概率是42%×90%=37.8%;AB至少接受一个的概率是58%，这种情况下接受C的概率是10%，可知AB至少接受一个且接受C的概率是58%×10%=5.8%。那么接受C方案的概率为43.6%。
可知三者概率为C>B>A。
因此，选择D选项。
【例3】小张和小王在同一个学校读研究生，每天早上从宿舍到学校有6:40、7:00、7:20和7:40发车的4班校车。某星期周一到周三，小张和小王都坐班车去学校，且每个人在3天中乘坐的班车发车时间都不同。问这3天小张和小王每天都乘坐同一趟班车的概率在：（ ）
A.3%以下
B.3%～4%之间
C.4%～5%之间
D.5%以上
【答案】C【解析】解法一：第一步，本题考查概率问题，属于基本概率。
第二步，概率=满足条件情况数÷总情况数，由于两人每个人每天的发车时间都不同，则可能的乘车选择总数为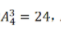
总情况数=24×24。要使两人车次相同，小张任意选择，小王选择与小张一样的即可，故总数为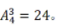
第三步，概率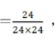
在4%~5%之间。
因此，选择C选项。
解法二：第一步，本题考查概率问题，属于分类分步型。
第二步，要使两人车次相同，小张任意选择，小王选择与小张一样的即可。第一天小张任意选，概率为1,小王在四个选择中只能选择与小张一致的，4选1,概率为1/4；同理，第二天小张任意选，概率为1,每天的发车时间都不同，小王3选1,概率为1/3；同理，第三天小张概率为1,小王概率为1/2。总概率为：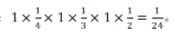
因此，选择C选项。
【例4】某单位的会议室有5排共40个座位，每排座位数相同。小张和小李随机入座，则他们坐在同一排的概率：（ ）
A.高于20%
B.正好为20%
C.高于15%但低于20%
D.不高于15%
【答案】C【解析】解法一：第一步，本题考查概率问题，属于基本概率。
第二步，先让小张随机入座，有40个座位可选；小李坐在同一排的选择有7种，随机入座的选择有39种，因此他们坐在同一排的概率为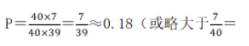
0.175）。
因此，选择C选项。
解法二：
第一步，本题考查概率问题，属于基本概率。
第二步，总情况数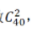
符合要求的情况数即五排中选一排再从该排中选两个座位，为
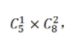则他们坐在同一排的概率为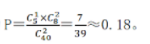
因此，选择C选项。
【例5】某次知识竞赛试卷包括3道每题10分的甲类题，2道每题20分的乙类题以及1道30分的丙类题。参赛者赵某随机选择其中的部分试题作答并全部答对，其最终得分为70分。问赵某未选择丙类题的概率为多少（ ）?
A.1/3
B.1/5
C.1/7
D.1/8
【答案】D【解析】第一步，本题考查概率问题，属于分类分步型。
第二步，根据部分试题作答并全部答对得70分，讨论情况可能为：
①丙类题1,乙类题2,有1种；
②丙类题1,乙类题1,甲类题2,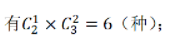
③乙类题2,甲类题3,有1种；共计8种。
第三步，未选择丙类题的有1种，故概率为1/8.因此，选择D选项。
通过上述例题的解题过程的展示，各位同学对概率问题一定有了更深刻的理解。对于我们通常所遇到的概率问题，我们可以根据题型特征选择使用古典概率或概率的分类和分步解题，一般情况下，可以找到满足条件的情况数和总的情况数即可用古典概率解题，若题中存在分类、分步过程，即可用概率的分类和分步解题，当然，有些题两种方法都适用，则选择其中较为简单的方法解题。
在解题过程中，若遇到概率间相互影响的题，可以依次讨论各种情况下的概率，再找到最终要求的概率。同时，在寻找满足条件的情况数和总的情况数时，通常会用到排列组合去计数，各位同学思路要清晰，这里的排列组合只是求解概率过程中的一个步骤。
最后，我们通过思维导图帮助大家梳理概率的相关知识点，希望对大家的备考有所帮助。
