行测数量关系考点——抓住几何问题的分数
几何问题是行测数量关系中的高频题型，如，正方形、长方形、圆形、三角形等平面图形的周长和面积，以及正方体、长方体、球体、圆柱体等立体图形的表面积和体积。还有一些是大家平时接触比较少，容易忽视的图形，如菱形、圆锥体。都是通过基本公式和性质来解题。
常考题型
1.一般几何问题（三角形、矩形、圆形、六边形等）
2.几何图形最值问题（面积最大、怎样走距离最短）
常考定理
1.两个三角形高相等，面积之比等于其底边长之比。
2.几何等比放缩性质：若边长（或半径）为n倍，则周长也为n倍，面积为n的2次方倍，体积为n的3次方倍。
3.周长一定，越接近圆，面积越大；反之，面积一定，越接近圆，周长越小；
4.表面积一定，越接近球，体积越大；反之，体积一定，越接近球，表面积越小。
5.两点之间直线距离最短。
常用解题方法
画图，考虑特殊角度、图形，做辅助线。
平面几何
周长公式：
正方形：C=4a
长方形：C=2（a+b）
圆形：C=2πr
扇形：C=弧长+2r=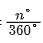
×2πr+2r
面积公式
正方形：S=a²
长方形：S=ab
圆形：S=πr²
扇形：S=πr²×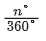
三角形：S=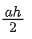
平行四边形：S=ah
菱形：S=对角线乘积/2
梯形：S=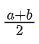
×h
立体几何
表面积公式
正方体：S=6a²
长方体：S=2（ab+ac+bc）
球体：S=4πr2 =πD2
圆柱体：S=2πr²+2πrh
球：S=4πr²=πd²
体积公式
正方体：V=a³
长方体：V=abc
球体：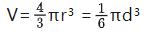
圆柱体：V=πr²h
圆锥：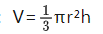
棱锥：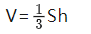
相似三角形理论
1.由圆周上某一点和圆的直径所组成的三角形一定是直角三角形。
2.相似三角形：
①判定：两个角相等，则两个三角形相似；
②结论：对应边成比例；面积之比=边长之比的平方。
3.勾股定理：a²+b²=c²
①常考勾股数：（3、4、5）、（6、8、10）、（5、12、13），当直角三角形边长为（6、8、10）、（5、12、13）时，其周长与面积相等；
②若直角三角形的三个角分别为30°、60°、90°时，则短直角边是斜边的一半；长直角边是短直角边的√3倍；
常用公式如下：
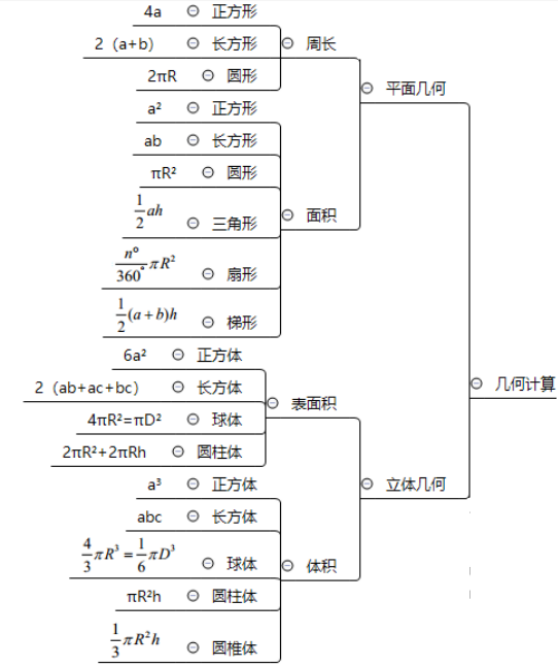
试题实例
1.一个长方形，若将短边长度增加4厘米，长边长度增加一倍，则面积是原来的3倍，若将长边缩短8厘米，就成正方形，则原长方形面积是多少平方厘米（ ）？
A.180
B.128
C.84
D.48
【答案】B【解析】第一步，本题考查几何问题，属于平面几何类。
第二步，设长方形的短边为x厘米，由长边缩短8厘米变成正方形可知，长为（x+8）厘米；根据面积是原来的3倍，可得2（x+8）×（x+4）=3（x+8）×x，解得x=8（厘米）。
第三步，故原长方形面积为（8+8）×8=128（平方厘米）。
因此，选择B选项。
2.一个高为10厘米，底面半径为5厘米的圆锥体塑料零件置于水中，底面朝上且水面平行，其浮出水面部分的高为2厘米。那么当该零件底面朝下且与水面平行置于水中时，浮出水面部分的高在以下哪个范围内？（零件始终不接触水底）（ ）
A．不到6厘米
B．6～7厘米之间
C．7～8厘米之间
D．超过8厘米
【答案】C【解析】第一步，本题考查几何问题。第二步，露出水面的高度为2，说明水下高度为8，那么排水体积为圆锥体积的（8÷10）3=64/125，倒置后浮力相同，排水体积也为圆锥体积的64/125，那么水面上的体积为圆锥的61/125，高度为圆锥的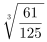
略小于0.8，故高度略低于8厘米。因此，选择C选项。
3.下图中，三个同心圆的半径分别为1厘米、2厘米、3厘米，AB与CD垂直且过圆心O。那么图中阴影部分面积与非阴影部分的面积之比是多少（ ）
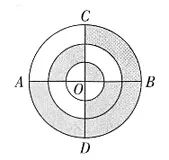
A.10:7
B.11:7
C.12:5
D.13:6
【答案】B【解析】将图中非阴影部分进行移动拼合后发现，非阴影部分可以看作由四分之一个大圆、四分之一个中圆和四分之一个小圆构成，面积为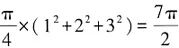
平方厘米，阴影和非阴影部分的总面积为32×π=9π平方厘米，则阴影部分面积为
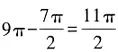，图中阴影部分面积与非阴影部分的面积之比为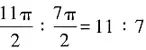
故本题选B。
