政华教育

【答案】A【解析】本题考查基础应用题，用方程法解题。设乙生产线月产量为x件，根据甲生产线月产量比乙多240件，可得甲生产线的月产量为（x+240）件；同理，设丙生产线月产量为y件，则丁生产线的月产量为（y+160）件。根据甲乙生产线效率之和等于丙丁生产线效率之和，可列方程：x+（x+240）=y+（y+160），化简得：y-x=40，即乙生产线的月产量比丙生产线少40件。因此，选择A选项。

02经济利润问题

【举个例子】从A市到B市的机票如果打6折，包含接送机出租车交通费90元、机票税费60元在内的总乘机成本是机票打4折时总乘机成本的1.4倍，问从A市到B市的全价机票价格（不含税费）为多少元（）？

A.1200

B.1250

C.1500

D.1600

【答案】C【解析】本题考查经济利润问题，属于利润率折扣类，用方程法解题。假设全价机票价格为x元，根据两次折扣的1.4倍关系可列式：即0.6x+90+60=1.4×（0.4x+90+60），可以得到x=1500（元）。因此，选择C选项。

03行程问题

【举个例子】甲车上午8点从A地出发匀速开往B地，出发30分钟后乙车从A地出发以甲车2倍的速度前往B地，并在距离B地10千米时追上甲车。如乙车9点10分到达B地，问甲车的速度为多少千米/小时（）？

A.30

B.36

C.45

D.60

【答案】A【解析】本题考查行程问题，属于相遇追及类。从题目中可知乙车的速度是甲车的两倍，即甲乙速度之比为1：2，在路程一定时，速度与时间呈反比，距离B市10千米时乙追上甲，甲比乙多走30分钟，最后总路程相等，则甲走了60分钟，乙走了30分钟。则乙再行驶40-30=10（分钟）到达了B市，则这一段路程甲需要20分钟=1/3小时，可知甲的速度=10÷（1/3）=30（千米/小时）。因此，选择A选项。

【拓展】利用选项相关性进行秒杀，乙速度是甲的2倍，选项A与D存在2倍关系，正确答案在二者之中，甲的速度为所求，选小的。

04工程问题

核心公式：工作总量=工作效率×工作时间。

常考题型：

基础公式型：用核心公式解题，常用方程法；

给定时间型：赋值法解题，给工作总量赋值；

效率制约型：赋值法解题，给效率赋值。

【举个例子】有甲、乙、丙三个工作组，已知乙组2天的工作量与甲、丙共同工作1天的工作量相同。A工程如由甲、乙组共同工作3天，再由乙、丙组共同工作7天，正好完成。如果三组共同完成，需要整7天。B工程如丙组单独完成正好需要10天，问如由甲、乙组共同完成，需要多少天（）？

A.不到6天

B.6天多

C.7天多

D.超过8天

【答案】C【解析】本题考查工程问题，属于效率类，用赋值法解题。设三者工作效率分别为甲、乙、丙，根据题意则有：2乙=甲+丙，3甲+3乙+7乙+7丙=7甲+7乙+7丙→3乙=4甲，赋值甲=3，则乙=4，解得丙=5。B工程总量=10丙=10×5=50，即甲乙合作需要50÷（3+4）=50/7（天），即7天多。因此，选择C选项。

05几何问题

常考平面几何、立体几何和几何构造。

平面几何：要求掌握三角形、正方形、矩形、圆形等周长、面积公式及几何性质。

立体几何：要求掌握正方体、长方体、球、圆柱、圆锥等立体图形表面积和体积公式及几何性质。

几何构造：是考试中比较难的题型，常用几何最值理论、几何性质等相关知识解题。

【举个例子】将一块长24厘米、宽16厘米的木板分割成一个正方形和两个相同的圆形，其余部分弃去不用。在弃去不用的部分面积最小的情况下，圆的半径为多少厘米（）？

A.2√2

B.4

C.3√2

D.8

【答案】B【解析】本题考查几何问题，属于平面几何类。根据分割成正方形和两个相同的圆，要所弃面积最小，由于正方形没有丢弃的面积，所以要使正方形的面积最大。将木板按下分割：

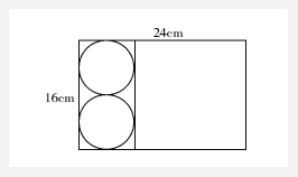
圆半径为（24-16）÷2==4（厘米）。因此，选择B选项。

06排列组合问题

排列：有序，用A计算，关键词“排序”；

组合：无序，用C计算，关键词“选择”；

分步：用乘法计算；

分类：用加法计算；

捆绑法：“必须挨着”先整体后内部；

插空法：“不能挨着”将不能挨着的插入到无要求中去；

隔板法：“将m个相同元素分成n份，每份至少分1个”通式为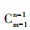

【举个例子】某单位要求职工参加20课时线上教育课程，其中政治理论10课时，专业技能10课时。可供选择的政治理论课共8门，每门2课时；可供选择的专业技能课共10门，其中2课时的有5门，1课时的有5门。问可选择的课程组合共有多少种（）？

A.5656

B.5600

C.1848

D.616

【答案】A【解析】本题考查排列组合问题，属于基础排列组合。政治理论课8门选择5门有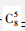=56（种）。专业技能可以分为3类情况：①2课时的5门全选；②2课时的5门选择4门，1课时的5门选择2门；③2课时的5门选择3门，1课时的5门选择4门，共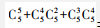=101（种），分步用乘法，56×101=5656（种）。因此，选择A选项。

07概率问题

核心公式：概率=满足条件的情况数/总情况数

常考题型：

基础公式概率：用核心公式解题；

枚举概率：用枚举法辅助求解概率；

分步分类：分步概率用乘法、分类概率用加法；

比赛概率：按最终获胜比分进行分类的概率；

反向概率：“正难则反”，1-反向概率。

【举个例子】小张和小王在同一个学校读研究生，每天早上从宿舍到学校有6：40、7：00、7：20和7：40发车的4班校车。某星期周一到周三，小张和小王都坐班车去学校，且每个人在3天中乘坐的班车发车时间都不同。问这3天小张和小王每天都乘坐同一趟班车的概率在：（）

A.3%以下

B.3%—4%之间

C.4%—5%之间

D.5%以上

【答案】C【解析】解法一：本题考查概率问题，属于基本概率。概率=满足条件情况数÷总情况数，由于两人每个人每天的发车时间都不同，则可能得乘车选择总数为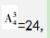总情况数=24×24。要使两人车次相同，小张任意选择，小王选择与小张一样的即可，故总数为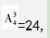概率=24/（24×24）=1/24，在4%—5%之间。因此，选择C选项。

解法二：本题考查概率问题，属于分类分步型。要使两人车次相同，小张任意选择，小王选择与小张一样的即可。第一天小张任意选，概率为1，小王在四个选择中只能选择与小张一致的，4选1，概率为1/4；同理，第二天小张任意选，概率为1，每天的发车时间都不同，小王3选1，概率为1/3；同理，第三天小张概率为1，小王概率为1/2。总概率为：1×（1/4）+1×（1/3）+1×（1/2）=1/24。因此，选择C选项。