
行测数量关系排列组合解题技巧
分类与分步
在各类公职考试的数量关系中,有一类比较特殊的问题——排列组合,之所以说特殊是因为它知识系统相对独立,研究问题的方法与对象也有所不同。大家往往会觉得它很难,遇到就放弃,但排列组合是一类计数问题,简单来讲就是统计方法数,还是有一些简单题的。那么,今天介绍的内容——分类与分布,是排列组合问题中比较重要的一环,也是比较简单的一部分内容。今天就和大家学习一下。
首先,我们要明确什么是分类与分步呢?他们是两种不同的计数原理。
1.加法原理(分类计数):做一件事情,完成它有N类方式,第一类方式有M1种方法,第二类方式有M2种方法,……,第N类方式有MN种方法,那么完成这件事情共有M1+M2+……+MN种方法。
2.乘法原理(分步计数):做一件事,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2不同的方法,……,做第n步有mn不同的方法。那么完成这件事共有N=m1*m2*m3*…*mn种不同的方法
下面我们通过例题来学习如何通过常用方法求解排列组合问题。
例题1:若每天从甲地到乙地分别有4趟航班、6列火车、3班长途汽车,则从甲地到乙地共有( )种不同的出行选择。
A.13
B.22
C.27
D.72
【答案】A【解析】从甲地到乙地,任选一趟航班、一列火车或一班长途汽车均能完成此事,是分类的过程。因此若想完成对“从甲地到乙地不同的出行选择”的计数,可分类讨论,结合题目描述,按不同出行方式分为三类:①坐飞机,有4种选择;②坐火车,有6种选择;③坐汽车,有3种选择。分类相加,故共有4+6+3=13种不同的出行选择,因此选择A项。
例题2:将4个不同颜色的锦囊放入3个不同的锦盒里,如果允许锦盒是空的,则所有可能的放置方法有( )种。
A.7
B.12
C.81
D.64
【答案】C【解析】只放1个锦囊不能完成此事,放2个、3个也不能完成此事,必须4个锦囊都放入锦盒才能完成此事,是分步的过程。第一步,确定第1个锦囊的放法,放在任意一个盒子里都是可行的,所以有3种放法;第二步,确定第2个锦囊的放法,同样放在任意一个盒子里都是可行的,所以也有3种放法;第三步,确定第3个锦囊的放法,同理有3种;第四步,确定第4个锦囊的放法,同理有3种。分步相乘,一共有3×3×3×3=81种不同的放法,选择C项。
通过上边两道题,相信大家已经能够掌握分类与分步啦,接下来,让我们来练习一下吧。
练习1:单位3个科室分别有7名、9名和6名职工。现抽调2名来自不同科室的职工参加调研活动,则有( )种不同的挑选方式。
A.22
B.66
C.159
D.378
【答案】C【解析】从三个科室中选两个科室共有三种分类方式:(7人,9人)、(7人,6人)、(6人,9人)。①选7人和9人的两个科室,第一步,从7人的科室中选1人,有7种选择,第二步,从9人的科室中选1人,有9种选择,共有7×9=63种选择。②选7人和6人的两个科室,第一步,从7人的科室中选1人,有7种选择,第二步,从6人的科室中选1人,有6种选择,共有7×6=42种选择。③选6人和9人的两个科室,第一步,从6人的科室中选1人,有6种选择,第二步,从9人的科室中选1人,有9种选择,共有6×9=54种选择。故共有63+42+54=159种挑选方式,因此选择C项。
练习2:世界非物质文化遗产高峰论坛召开记者会,共有10家国内媒体和4家国外媒体参加。组委会从中选出3家媒体回答他们的问题,要求这3家媒体中既有国内媒体又有国外媒体,且国内外媒体交叉提问,则不同的提问方式有:( )
A.240种
B.360种
C.480种
D.1440种
【答案】C【解析】提问方式共有(国内、国外、国内)和(国外、国内、国外)两种顺序。其中(国内、国外、国内)有10×4×9=360种;(国外、国内、国外)有4×10×3=120种。共有360+120=480种,因此选择C项。
相信通过今天的学习,大家已经熟练掌握了分类与分步。希望大家在遇到排列组合问题后不再畏惧排列组合,把题干分析清楚,利用一些小技巧来解决排列组合问题。当然大家还需要通过大量练习来真正熟练掌握这类方法,在解题过程中提升解题速度!
排列组合常用方法总结
优限法
当元素有绝对的位置要求时使用:第一步安排特殊元素,第二步解决其他元素。
例:一次会议某单位邀请了10名专家,该单位预定了10个房间,其中一层5间、二层5间。已知邀请专家中4人要求住二层、3人要求住一层、其余3人住任一层均可。那么要满足他们的住房要求且每人1间,有多少种不同的安排方案( )?
A.75
B.450
C.7200
D.43200
【答案】D【解析】题干中4人要求住二层、3人要求住一层,优先安排这7名专 家的房间,其余3人放在最后。4人要求住二层,其方法数为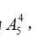 3人要求住一层,其方法数为
3人要求住一层,其方法数为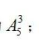 其余3人安排住剩下的3个房间,其方法数为
其余3人安排住剩下的3个房间,其方法数为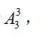 故共有
故共有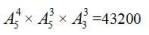 种不同的安排方案。
种不同的安排方案。
捆绑法
当元素必须相邻时使用:第一步把相邻元素看成一个整体(保证相邻),并且和其他元素进行排列,第二步确定整体内元素的顺序。
例:为加强机关文化建设,某市直机关在系统内举办演讲比赛,3个部门分别派出3、2、4名选手参加比赛,要求每个部门的参赛选手比赛顺序必须相连,问不同参赛顺序的种数在以下哪个范围之内( )?
A.小于1000
B.1000~5000
C.5001~20000
D.大于20000
【答案】B【解析】题干要求每个部门的参赛选手比赛顺序必须相连,可以先把每 个部门的参赛选手分别捆绑起来看成3个整体进行安排,再考虑部门内部选手的顺序。首先 考虑三个部门的出场顺序,有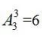 种;其次考虑每个部门选手的出场顺序,分别有
种;其次考虑每个部门选手的出场顺序,分别有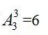 种,
种,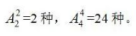 则不同参赛顺序的种数为6×6×2×24=72×24,计算结果显然大于1000,小于5000,故此题答案为B。
则不同参赛顺序的种数为6×6×2×24=72×24,计算结果显然大于1000,小于5000,故此题答案为B。
插空法
当元素不能相邻时使用:第一步安排不相邻以外的元素(形成空隙),第二步将不能相邻的元素插入空隙中(确保不相邻)。
例:把12棵同样的松树和6棵同样的柏树种植在道路两侧,每侧种植9棵,要求每侧地柏树数量相等且不相邻,且道路起点和终点处两侧种植的都必须是松树。问有多少种不同的种植方法( )?
A.36
B.50
C.100
D.400
【答案】C【解析】道路每侧种植9棵树,其中6棵松树3棵柏树,6棵松树形成 5个空隙,选择3个空隙并将3棵柏树放入有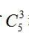 种方法,因为有两侧,故共有
种方法,因为有两侧,故共有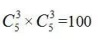 种不同的种植方法。
种不同的种植方法。
间接法
当正面解题情况复杂,而问题对立面情况比较容易计算时使用(题干出现“至少”“至多”等描述字眼):第一步分别计算整体情况数和对立面的情况数,第二步将两者做差。
例:某单位有甲和乙2个办公室,分别有职工5人和4人。每周从这9名职工中随机抽取1人下沉社区担任志愿者(同一人有可能被连续、重复选中)。问7月前2周的志愿者至少有1人来自甲办公室的安排有多少种( )?
A.65
B.81
C.16
D.32
【答案】A【解析】根据题意可知,7月前2周的志愿者总情况数为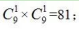 7 月前2周的志愿者均来自乙办公室的情况数为
7 月前2周的志愿者均来自乙办公室的情况数为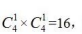 因此所求81-16=65。
因此所求81-16=65。
通过上面的方法介绍和对应题目练习,相信大家对于排列组合的常用方法有了更深的理解,后续还是需要不断巩固练习,方能驾轻就熟,彻底地啃下这块硬骨头!








