
行测数量关系快速解题技巧
一、赋值总量类工程问题
1.题型特征
题干中给出多个主体(≥2)针对同一项工程的不同完工时间。
2.解题思路
①将工作总量赋值为完工时间的公倍数;
②根据效率=总量/时间,计算各主体效率;
③根据题意列式求解。
3.总结
判定一道题是否属于赋值总量类工程问题,要看是否有针对同一项工程的两个或以上的不同完工时间,分成几部分完成一项工程的不属于完工时间。赋总量时,只要是完工时间的倍数,随便多大都行,甚至不找倍数,赋总量为1、2、3,理论上都是可以的,但是解题时肯定是怎么简单怎么来,因此优先找最小公倍数。
4.典型例题
【2018江苏】手工制作一批元宵节花灯,甲、乙、丙三位师傅单独做,分别需要40小时、48小时、60小时完成。如果三位师傅共同制作4小时后,剩余任务由乙、丙一起完成,则乙在整个花灯制作过程中所投入的时间是:( )
A.24小时 B.25小时
C.26小时 D.28小时
【解析】
【答案:A】出现甲乙丙三人的完工时间,即为赋值总量类工程问题。
(1)赋总量:计算最小公倍数可用短除法或扩大法,求出最小公倍数为240,将总量赋值为240。
(2)求效率:效率=总量/时间,则甲的效率为240/40=6、乙的效率为240/48=5、丙的效率为240/60=4。
(3)列式求解:因“三位师傅共同制作4小时”,即工作量=效率×时间=4×(6+5+4)=60。根据“剩余任务由乙、丙一起完成”,则需要时间t=(240-60)/(5+4)=20小时。20是乙丙合作的时间,求的是乙投入的总时间,则乙的总时间为4+20=24小时,对应A项。
二、赋值效率类工程问题
1.题型特征
①题干中直接给出效率比例关系,或通过题干条件可计算出各主体效率比例;
②题干中出现相同的多个主体,如50个人修路,30台机器收割麦子等。
2.解题思路
①求出效率比例,将比例赋值为各主体效率;给出多个相同主体的,将所有主体的效率默认相等,赋值为1;
②根据总量=效率×时间,求出总量;
③根据题意列式求解。
3.总结
近年来常考的题目中,题干一般没有直接给出主体之间的效率比例关系,往往给出相同时间内各主体完成工作量之比,或相同工作量所用不同时间,此时可根据题干条件求出效率比例。求出比例进行赋值时,尽量将效率赋值为整数。
4.典型例题
【2016国考】某浇水装置可根据天气阴晴调节浇水量,晴天浇水量为阴雨天的2.5倍。灌满该装置的水箱后,在连续晴天的情况下可为植物自动浇水18天。小李6月1日0:00灌满水箱后,7月1日0:00正好用完。问6月有多少个阴雨天?( )
A.10 B.16
C.18 D.20
【解析】
【答案:D】虽未出现工程等字样,但水箱浇水为消耗的过程,可理解为工程问题。题干出现“晴天浇水量为阴雨天的2.5倍”,即给出晴天与阴天浇水量效率比,可判定为给定效率比例关系类工程问题。
(1)赋效率:晴天浇水量为阴雨天的2.5倍,则赋值晴天效率为5、阴天效率为2。
(2)求总量:“在连续晴天的情况下可为植物自动浇水18天”,则总量=18×5=90。
(3)列式求解:6月为30天,设其中阴天x天,则晴天为(30-x)天。根据题意,90=阴天浇水量+晴天浇水量=2x+5×(30?x),解得x=20天,对应D项。
三、给具体值类工程问题
1.题型特征
题干中出现效率或总量的具体值。
2.解题思路
①设未知数(求谁设谁、设小不设大、设中间量);
②根据工作过程列方程求解。
3.典型例题
【2018北京】甲、乙两人生产零件,甲的任务量是乙的2倍,甲每天生产200个零件,乙每天生产150个零件,甲完成任务的时间比乙多2天,则甲、乙任务量总共为多少个零件?( )
A.1200 B.1800
C.2400 D.3600
【解析】
【答案:B】给出了效率的具体值,需设未知数列方程求解。
因“甲完成任务的时间比乙多2天”,为了方便计算,设小不设大,设乙的工作时间为t天,则甲的时间是(t+2)天。列式为:200×(t+2)=2×150×t,解得t=4天。因此乙的工作量=150×4=600个,甲的工作量=600×2=1200个,则总量=1200+600=1800个,对应B项。
4.拓展
1.近几年的考试中给出具体效率的题目考查比较多,此类题比较简单,类似于和差倍比问题。根据题目直接列方程求解,核心点在于需注意不变和相等,比如工作总量相等或时间不变。
2.设未知数时结合题意进行分析,缺谁设谁,本题中有效率,缺少总量与时间,若按照求谁设谁,设总量为x,则时间为x/200,此时后续计算会比较繁琐,因此不建议设总量为x。设未知数的方法要根据题干灵活选择。
数量关系超实用的7种必杀技巧!
说到行测最难的模块,相信很多小伙伴们会把心中的这一票投给数量关系。其实,数量关系并非洪水猛兽,今天就给大家介绍7种数量关系的秒杀技巧!
1.“七种武器”之代入排除法
代入排除是一种易于被广大考生操作的方法,是数学运算的第一方法。是正向的思维,本质上是一种验证的方法,对思维的要求比较低,在考试的时候非常有用。
【例题】甲、乙、丙、丁四个人分别住在宾馆1211、1213、1215、1217和1219这五间相邻的客房中的四间里,而另外一间客房空着。已知甲和乙两人的客房中间隔了其他两间客房,乙和丙的客房号之和是四个人里任意二人的房号和中最大的,丁的客房与甲相邻且不与乙、丙相邻。则以下哪间客房可能是空着的?( )
A.1213 B.1211
C.1219 D.1217
【解析】本题条件给的比较多,而且很乱,不好直接入手。这时如果考生想到用代入排除去验证下,就会发现题目变得很简单了,答案为D。
2.“七种武器”之数字特性
整除、倍数等数字特性是数学运算里最基础的内容,应用范围非常广泛,有时甚至有秒杀的效果。对此,广大考生需要通过大量练习以获得敏感度,从而能够灵活运用。
【例题】某公司6名员工一起去用餐,他们各自购买了三种不同食品中的一种,且每人只购买了一份。已知盖饭15元一份,水饺7元一份,面条9元一份,一共花费了60元。问他们中最多有几人买了水饺?( )
A.1 B.2 C.3 D.4
【解析】本题可利用方程法进行求解。不定方程的解法通常有以下两种:一种是利用奇偶性和尾数法进行求解;另一种是利用因子特性进行求解。根据题意,可设买该法、水饺、面条的人数分别为X、Y、Z,可得15X+7Y+9Z=60;X+Y+Z=6;利用第一个方程,易知15、9、60都含有因子3,所以7Y也含有因子3,而7不含有因子3,所以Y必含有因子3,即Y必是3的倍数。结合选项,秒杀C。
3.“七种武器”之赋值法
当题目中没有出现具体的值,只是给了一些相对量比如倍数、分数等时,可以赋值某些量以简化计算。
【例题】某集团有A和B两个公司,A公司全年的销售任务是B公司的1.2倍。前三季度B公司的销售业绩是A公司的1.2倍,如果按照前三季度的平均销售业绩,B公司到年底正好能完成销售任务。问如果A公司希望完成全年的销售任务,第四季度的销售业绩需要达到前三季度平均销售业绩的多少倍?( )
A.1.44 B.2.76 C.2.4 D.3.88
【解析】题中没有给出具体数值,考虑赋值。设A前三季度完成100,则B前三季度完成120,则B全年完成120/3+120=160,则A全年完成192,可得A第四季度完成92,前三季度平均完成,则第四季度业绩是前三季度平均值的92/(100/3)=2.76。因此,本题选B。
4.“七种武器”之捆绑插空法
在排列组合问题中,若要求元素相邻,把要求相邻的元素捆起来看做一个元素;若要求元素不相邻,把这些元素插入一些空隙中,这是排列组合问题最常用的两种技巧。
【例题】为加强机关文化建设,某市直机关在系统内举办演讲比赛3个部门分别派出3、2、4名选手参加比赛,要求每个部门的参赛选手比赛顺序必须相连,问不同参赛顺序的种数在以下哪个范围之内?( )
A.大于20000 B.5001-20000
C.1000-5000 D.小于1000
【解析】每个部门的参赛选手比赛顺序必须相连,体现“相邻”原则,考虑捆绑法。将3个部门分别看成一个整体,进行排序,图片;然后3个部门内部各自排序,依次图片、图片;为分步用乘法,可得6×6×2×24=1728。因此本题选C。
5.“七种武器”之代入排除法
在数量关系题目中,有些题目需要考生数出有多少种情况,如果发现选项数据不大,可以直接进行枚举;如果选项数据较大,一般是枚举几个比较简单的情况,然后找到规律归纳出一般情况。
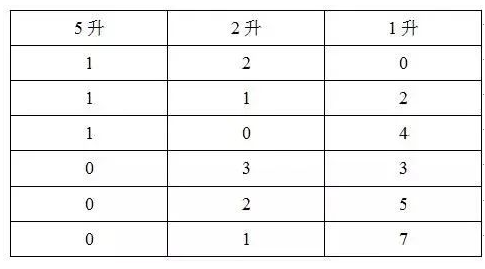
【例题】餐厅需要使用9升食用油,现在库房里库存有15桶5升装的,3桶2升装的,8桶1升装的。问库房有多少种发货方式,能保证正好发出餐厅需要的9升食用油?( )
A.4 B.5 C.6 D.7
【解析】枚举如下,答案为C。
6.“七种武器”之特殊拐点法
近两年国考数量关系都出现的图形题,解决这类问题最快的方法就是找到几个特殊的拐点,结合选项进行验证就能快速的锁定答案。
【例题】某学校组织学生春游,往返目的地时租用可乘坐10名乘客的面包车,每辆面包车往返的租金为250元。此外,每名学生的景点门票和午餐费用为40元,如果求尽可能少租车,则以下哪个图形最能反映平均每名学生的春游费用支出与参加人数之间的关系?( )
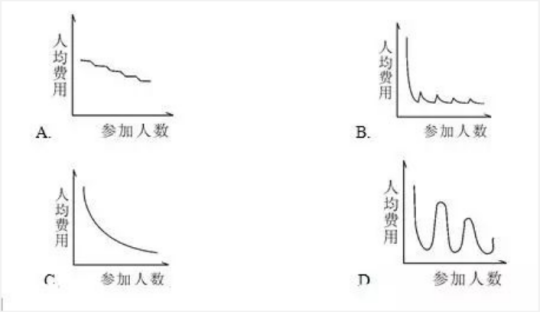
【解析】结合图形,代入人数等于1、10、11即可判断正确答案为B。
7.“七种武器”之蒙题法
在数量关系中,总有一些题目无法下手或者思考良久也未能明白其意,这种情况下,放弃也是一种智慧。
通常情况下,命题人为了避免某些考生在蒙的时候撞大运,四个选项出现的频率基本相当,基于这样的原则,那些不会做或者没时间做的题我们就直接蒙出现次数少的选项就可以了。








