
行测备考资料-数量关系
学会逆向思考,巧解数量问题
行测考试中关于数量关系的一些题目,大家从常规思路或者正向思考去解决问题时往往比较困难和麻烦,这种情况下,如果我们能够学会逆向思考,那么很多题目求解起来就能节约不少的时间,那么接下来一起来看一下这样一种逆向思考的方法。
例题感知
例题1:由数字1、2、3、4、5组成无重复数字的五位数,问万位和千位上至少有一个奇数的五位数有几个?
A.12 B.54 C.108 D.120
解析:这是一道排列组合类型的题目,我们会发现,题目中要求万位和千位至少有一个奇数,那么可能就会存在以下几种情况:万位是奇数千位不是;万位不是奇数千位是;万位和千位都是奇数。情况越多我们在列式和计算时就越麻烦。那这个题目有没有简单的方法呢?其实我们可以逆向考虑,万位和千位至少有一个是奇数,它的反面情况就是万位和千位都不是奇数而全都是偶数,那我只要求出这一种情况,用总的方法数减掉反面的情况就可以了,所以可以列式为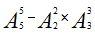 =120-12=108选择C。
=120-12=108选择C。
通过这个题目我们会发现,如果一个题目从正面去思考比较麻烦时,我们可以逆向用思维来求解,题目就会简单很多。除了排列组合问题,其他类型的题目也是可以应用这个思想的,我们来练习这样一道题目。
例题2:某单位从包括甲乙在内的5名应聘者中招聘3人,如果这5名应聘者被录用的机会均等,则甲乙两人中至少有1人被录用的概率是多少?
A. B. C. D.
解析:这是一道概率类型的题目,题目中要求甲乙至少有一个人被录用,那么可能就会存在以下几种情况:录用甲不录用乙;录用乙不录用甲;甲乙都被录用。同样这个题我们可以逆向考虑,甲乙至少有一人被录用,它的反面情况就是甲乙都没被录用,就可以用总概率1减掉反面的概率,所以可以列式为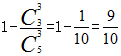 选择D。
选择D。
通过这两个题目,希望大家能够了解逆向的思想,在遇见一些正面求解比较困难的题目时,能够利用这种思想,简化解题步骤,节约做题时间!
理解性记忆多次独立重复试验
在行测概率问题中,经常会出现多次独立重复试验模型的考查,但是对于多次独立重复试验模型的公式,很多同学都觉得公式太长,里面涉及到的字母太多很容易套错,所以今天带大家理解性地记忆一下这个公式。
多次独立重复试验指的是一个试验重复n次,每次的结果之间互不影响,求其中A事件(发生一次的概率为P)发生m次的概率。在这里我们可以分为三个步骤进行记忆:
1. 在重复n次试验的过程中,我们并不能够确定具体是哪些次A事件发生,所以A事件发生m次本身会有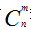 种可能性;
种可能性;
2. 确定了发生次数后我们就可以计算A事件发生的概率,A发生一次概率为P,发生m次概率为m个P相乘,即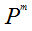 ;
;
3. 剩余次数我们不能再让A发生了,所以还要计算A不发生的概率,A不发生一次的概率为1-P,不发生n-m次,即(1-P)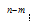 ;
;
我们把三步综合在一起,公式即为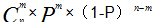 。在我们后续的解决问题的过程中,就按照上述步骤求解问题就可以了。
。在我们后续的解决问题的过程中,就按照上述步骤求解问题就可以了。
【例1】掷一枚骰子5次,问这5次中有4次出现6点的概率?

【答案】D。解析:题目求5次掷骰子试验中6点出现4次的概率,求多次独立重复试验我们理解性套公式。第一步,在5次掷骰子中具体是哪4次出现6点未知,共有 种可能性;第二步,出现6点一次概率为
种可能性;第二步,出现6点一次概率为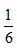 ,出现6点4次概率为
,出现6点4次概率为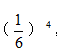 ,第三步,还有一次不是6点,再乘上不是6点的概率
,第三步,还有一次不是6点,再乘上不是6点的概率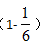 ,即结果为
,即结果为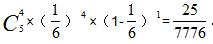 所以本题选择D选项。
所以本题选择D选项。
【例2】射击运动员每次射击命中10环的概率是80%,5次射击有4次命中10环的概率是( )。
A.80% B.63.22% C.40.96% D.32.81%
【答案】C。解析:题目求5次射击试验中命中10环4次的概率,求多次独立重复试验我们理解性套公式。第一步,在5次射击中具体是哪4次10环未知,共有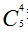 种可能性;第二步,命中一次概率为80%,命中4次概率为
种可能性;第二步,命中一次概率为80%,命中4次概率为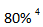 ;第三步,还有一次未命中10环,再乘上未命中的概率(1-80%),即结果为
;第三步,还有一次未命中10环,再乘上未命中的概率(1-80%),即结果为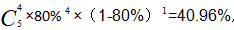 所以本题选择C选项。
所以本题选择C选项。
以上就是我们如何理解性记忆多次独立重复试验的公式,同学们只要理解性的刷一部分题目后,相信大家以后再也不会有记不住此公式的困扰。
乘风破浪的小方法——方程法
数量关系在行测考试中的题型是很多样的,变化方式也是多种的,也是考生一直头疼的题型,今天给大家介绍一种方法,不是新的方法,但确很好用,想要考试中披荆斩棘,乘风破浪的小方法用起来吧。
方程法
核心:寻找等量关系
操作步骤:设未知数-列方程-解方程-作答
例题展示
例1:甲、乙、丙三瓶酒精溶液的质量比为1:2:3.若将甲瓶中的溶液全部倒入乙瓶,则乙瓶溶液的浓度将变为原来的2倍,此时再将乙瓶中的混合溶液全部倒入丙瓶,则丙瓶溶液的浓度将变为原来的3倍。问原来甲丙两瓶酒精的浓度之比为( )
A.10:1 B.8:3 C.5:2 D.4:1
【解析】A。由题目的描述,两次混合以后出现了倍数关系,是比较明显的等量关系,根据甲、乙、丙的质量比,可以假设三瓶溶液的质量分别为1、2、3,设浓度为x、y、z,根据甲乙混合后的浓度为乙原来2倍,可得x+2y=(1+2)×2y,化简得x=4y;根据甲、乙混合溶液与丙混合后的浓度为丙原来浓度的3倍,可得(1+2)×2y+3z,化简得2y=5z。因此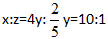 。
。
例2. 三位专家为10幅作品投票,每位专家分别都投出了5票,并且每幅作品都有专家投票。如果三位专家都投票的作品列为A等,两位专家投票的列为B等,仅有一位专家投票的作品列为C等,则下列说法正确的是( )
A.A等和B等共6幅 B.B等和C等共7幅
C.A等最多有5幅 D.A等比C等少5幅
【解析】根据题目的描述,存在两个等量关系,总共10幅作品,投票数为15票,可以设A等、B等、C等作品数分别为a,b,c,则有:a+b+c=10,3a+2b+c=15,第二个式子减掉第一个式子,有(3a+2b+c)-(a+b+c)=2a+b=5,a从0开始代入,可以取0、1、2,解得符合要求的解有三组,a=0,b=5,c=5;a=1,b=3,c=6;a=2,b=1,c=7,观察选项只有D符合要求。
注重题干的分析,出现了等量关系的描述,就可以借助方程的方法求解问题。题干中没有的量可以设未知数,根据等量关系,列方程解方程。
“交替合作”带你“斗笑”行测成绩
很多考生在复习行测数量关系时,总觉得只要自己仔细思考,大部分题还是能做出来的,但做的比较慢,所以在考试中总会费一些时间,但众所周知,对于行测考试,做题速度很重要。那我们怎样才能够提升做题速度呢?其实对于数量关系,只要我们掌握一些常用的技巧,就可以做到既快又准。今天在这里给大家介绍一下有关数量中交替合作的相关知识点与常见考法,帮您既快又准地拿下相关题目,让您对考试成绩一路“斗笑”且不停。
一、交替合作的定义
交替合作指的是在多方合作工作中,一方工作时,其余方均不工作。它分为两种情况,一种是出现的都是正效率,另一种是有正效率也有负效率。
注:无论哪种情况,关键点都是找出最小的循环周期及一个循环周期的效率和。
二、交替合作的基本公式
 =循环周期数...剩余工作量 (只有正效率)
=循环周期数...剩余工作量 (只有正效率)
三、交替合作的常见考法
例题:一条隧道,甲单独挖要20天完成,乙单独挖要10天完成。如果甲先挖1天,然后乙接替甲挖1天,再由甲接替乙挖1天......两人如此交替工作。那么,挖完这条隧道共用多少天?( )
A.13 B.13.5 C. 14 D.15.5
【答案】:选B。解析:由题知该题为交替合作的工程问题,已知不同的人完成同一项工作的不同时间,所以设工作总量为时间的最小公倍数20,可求出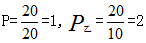 ,所以甲、乙的效率和为
,所以甲、乙的效率和为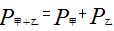 =+=1+2=3循环周期为甲、乙各一天,共2天,所以循环周期数=
=+=1+2=3循环周期为甲、乙各一天,共2天,所以循环周期数=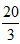 =6...2,即为6个整的周期,共对应12天,余2个工作量,即甲先做1个,接着乙再做1个,甲完成1个工作量需要1天,乙完成1个工作量需
=6...2,即为6个整的周期,共对应12天,余2个工作量,即甲先做1个,接着乙再做1个,甲完成1个工作量需要1天,乙完成1个工作量需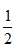 天,所以共需要
天,所以共需要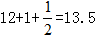 天。故答案为B。
天。故答案为B。
以上介绍的“只含正效率的交替合作的解题方法”,小伙伴们了解并熟练运用后就能够轻松解决数量关系中涉及到的相关题目,达到快做快对的目的,助力大家成绩一路“正效率”!
摘掉根号的帽子”——巧解行测数字推理中根式数列问题
根式数列是近些年江苏省考数字推理中基本每年都会考察一道题目。因为根式数字本身的特殊性,戴上根号帽子的它可以呈现不同的形式,所以它在计算以及规律的推导上和常规的整数有所区别。那么,当我们在考试的时候,如何能够快速的判断出根式数列考察的规律并且选出正确的答案呢?接下来通过几道例题来寻找一下快速解题的方法吧。
例1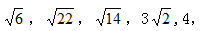 ( )
( )

【解析】B。观察数列,前三项数字都在根号下,不妨先将题干中所有数字统一转化为根式: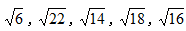 观察根号内数字规律,后项-前项可得16,-8,4,-2,是公比为-1/2的等比数列,则下一项=
观察根号内数字规律,后项-前项可得16,-8,4,-2,是公比为-1/2的等比数列,则下一项=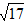 。
。
例2.3,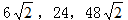 ,( )
,( )
【解析】D。观察根号下数字可以发现,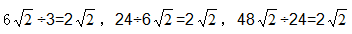 ,故题干构成公比为
,故题干构成公比为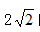 的等比数列。下一项为
的等比数列。下一项为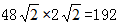
例3.1,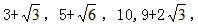 ( )
( )
【解析】C。题干中每个数字由加号构成,观察左边为1,3,5,( ),9,推导中间为7,故10可以写为7+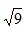 ,则所求项左边为11,右边为0,
,则所求项左边为11,右边为0,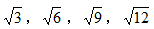 ,( ),所求项右边为
,( ),所求项右边为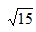 故答案为11+
故答案为11+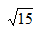 。
。
例4. 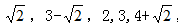 ,( )
,( )

【解析】C。题干中有加号有减号,信息比较复杂,但根号下数字相同,且数列中间存在2和3,不妨考虑整体做加减。做完减法结果为: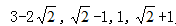 ,( )发现新数列构成了公比为
,( )发现新数列构成了公比为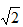 +1的等比数列,故下一项为
+1的等比数列,故下一项为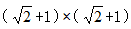 结果为3+2则所求项为
结果为3+2则所求项为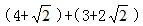 =
=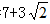 。
。
通过四道例题给我们呈现了根式数列四种不同的推导方式,看似很复杂,其实规律性非常明显:
(一)例1和例2都不含有加减符号,当根号下数字不同时,我们可以将根号外的数字全部化入根号内寻找规律;而当根号下数字相同时,我们可以通过做除法找出规律。
(二)例3和例4都含有加减符号,当根号下数字不同时,我们可以将加减符号两边分开找规律;而当根号下数字相同时,可以选择做加减找出规律。








