政华教育

容斥问题在你眼中是否繁琐呢?采用容斥问题的公式或者借助文氏图分析，相信双通道可帮助同学们绕出容与斥的复杂;极值问题是否也带给你困扰?常见和定求最值、为保证完成目的的最不利分析、行走最短路程的探索等，协助了同学们一点点熟知极值的脾性。而容斥问题与极值问题共同孕育的容斥极值，让多集合在全集中使劲挤兑，数量关系与资料分析的考查中，它皆是常客。很多同学感觉它走出了繁琐与困扰，有些负负得正的韵味。如何分析应用呢?

例题1：在阳光明媚的一天下午，甲乙两人给30盆花浇水，已知甲浇了20盆花，乙浇了17盆花。假设甲乙两人给每盆花浇水量相同，且每盆花浇水不宜过量，若重复浇水需放到室外光照、风量较好处养护，那么两人浇水后至少搬至室外多少盆花?

A.3 B.5 C.7 D.9

【解析】正确答案为C。共有30盆花，甲浇了20盆花，乙浇了17盆花，所以必会存在两人均浇过的花，即重复浇水需移至室外养活的花。根据两者容斥问题的公式：I=A+B-A∩B+M，即30=20+17-A∩B+M，得A∩B=7+M。若要A∩B最小，那么M的值也要尽可能小，M最小可取0，此时A∩B最小为7，故本题选C。(注：I表示全集，A、B分别表示全集中的两个集合，M表示既不属于集合A也不属于集合B的部分，即补集)

在花朵都如此有求生欲的今天，这一题在考场上又怎会不宝贵呢?但经过分析可知此题的计算难度并不高，所求为两集合公共部分的最小值，即在全集中既不属于A集合也不属于B集合的M取得0的前提下求得(A∩B)min=A+B-I。以此类推，若在容斥中求极值，则全集中多集合间公共部分的最小值分为：

(A∩B)min=A+B-I;

(A∩B∩C)min=A+B+C-2I

(A∩B∩C∩D)min=A+B+C+D-3I

……

例题2：2019年年末全国大陆总人口140005万人，比上年末增加467万人，其中，城镇常住人口84843万人，占总人口比重(常住人口城镇化率)为60.60%，比上年末提高1.02个百分点。户籍人口城镇化率为44.38%，比上年末提高1.01个百分点。全国人户分离的人口占大陆总人口的20%，其中，84.29%为流动人口。

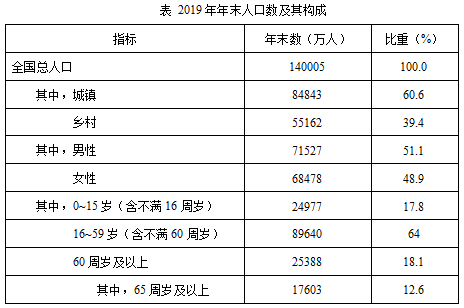
问题：2019年年末，城镇常住人口中，男性人口占比至少为：

A.5.2% B.11.7% C.17.5% D.19.3%

【解析】正确答案为D。所求为城镇常住人口中的男性人口占比，由表格可知，2019年年末，城镇常住人口占全国总人口比重为60.6%，男性人口占全国总人口比重为51.1%，则既是城镇常住人口又是男性人口占总人口的比重至少为60.6%+51.1%-1=11.7%，则城镇常住人口中，男性人口至少占11.7%÷60.6%≈19.3%，选择D项。

行测最不利原则问题的解题方法

公务员考试行测中，很多考生面对数量关系的题目时总是束手无策，甚至没有花时间去思考就直接全选了某一选项，因为大家总觉得数量关系的题目太难了，其实有部分题目是很简单，套路性很强的，是建议大家挑出来做的，比如接下来我们所要学习的最不利原则问题的题目，就是建议大家挑出来做的。那什么是最不利原则问题呢，又该怎么解决呢?今天就来帮助大家掌握这一解题技巧。

一、题型特征

问法中出现“至少……保证”

二、解题方法

最不利的情况数+1

注：最不利的情况即让保证发生的事情“尽量不发生”

三、例题展示

【例1】从一副完整的扑克牌中，至少抽出多少张才能保证抽到2张花色相同的牌?

A.2 B.3 C.5 D.7

【答案】D。

【解析】

(1)若问怎么才能保证抽到2张花色相同的牌?全部抽完，可以保证，但不是至少的情况;

(2)若问至少抽几张，可以抽到2张花色相同的牌?抽2张就有可能是2张花色相同的牌，但没法保证。

那为什么抽2张、3张、4张都不能保证抽到2两张花色相同的牌呢?因为存在不发生的可能性。所以要想保证的话，就需要把所有可能不发生的情况都找到，也就是让保证的事情“尽量不发生“”，然后再取一张就一定能保证发生了。

四种花色各抽1张，这个时候再取一张，因为有大小王，也没法保证抽到2张花色相同的牌，需要把2张王也抽出，这样所有不可能的情况都取完了，再取1张，就一定是有2张花色相同的牌，故至少取6+1=7张牌，才能保证有2张花色相同的牌。

注：出现“至少……保证”，就考虑“尽量不发生”，把所有可能不发生的情况都取完，即找到最不利的情况，然后“最不利的情况数+1”即为答案。

【例2】从一副完整的扑克牌中，至少抽出多少张才能保证抽到6张花色相同的牌?

【答案】23。

【解析】问法中出现“至少……保证”，明确是最不利原则问题。保证抽到6张花色相同的牌，尽量不让事情发生，也就是当四种花色全都抽出了5张，大小王也都抽出之后，所有可能不发生的情况都找到了，也就是找到了最不利的情况，然后再抽1张，一定会有6张牌的花色相同，故4×5+2+1=23。

注：“尽量不发生”就考虑每样少给一个，即最不利的情况为“数字-1”

【例3】一堆扑克牌当中有12张黑桃的，10张红桃的，6张梅花的和4张方块的，从中至少抽出多少张才能保证抽到9张花色相同的牌?

【答案】27。

【解析】问法中出现“至少……保证”，明确是最不利原则问题。每种花色各取8张，但是，梅花和方块数量不够8张，如果不管他们的话，从黑桃和红桃各取8张，如果再取一张就有可能是梅花和方块，就无法保证抽到9张花色相同的牌，所以最不利的情况应该是黑桃和红桃各取8张，不够8张的梅花和方块全取，所以至少取出8×2+6+4+1=27张，才能保证抽到9张花色相同的牌。

注：如果够就每样少给一个，如果不够就全部取出

所以，最不利原则问题的解题核心就是让保证发生的事情，尽量不发生，把所有可能不发生的情况都考虑到，也就是找到“最不利的情况”，然后“最不利的情况数+1”即可，相信大家通过一定量的题目练习都能够轻松掌握这一解题技巧，在行测考试中轻松求解。

方阵问题中的小规律

在公务员考试中行测数量关系的这一部分有一种独特的数学模型我们称之为“方阵问题”，这类题目在实际的考查中相对会比较灵活多变，还是让很多同学望而生畏，但其实只要我们掌握了其中的规律就可以轻松应对。

首先我们要认识什么样的问题才是方阵问题，方阵其实是一种队形，一个队伍排队，横着排叫行，竖着排叫列，若行数与列数都相等，正好排成一个正方形，这种队形就叫做方阵。将一些物体按照这样的方式排列起来，也叫做方阵。方阵分为实心方阵和空心方阵两种，无论是哪种方阵在考试中都是围绕方阵的层数、每层人数、总人数来展开问题的。

方阵问题主要对应以下几条规律，同学们一定要牢记：

1、每层人数=4×(每边人数-1)

2、每层每边人数依次增加2

3、每层总人数依次增加8(行人数为奇数的最内层除外)

4、实心方阵总人数=最外层每边人数的平方

那么具体如何应用呢?实心方阵与空心方阵的区别再哪儿?我们来看下面的例题。

【例题1】若干学校联合进行团体操表演，参演学生组成一个方阵，已知方阵由外到内第二层有104人，则该方阵共有学生( )人。

A.625 B.841 C.1024 D.1369

【解析】此题是一个实心方阵的例题，已知由外到内第二层有104人，通过每层总人数依次增加8可知最外层有104+8=112人，又通过每层人数=4×(每边人数-1)可知该方阵最外层每边有29人，所以总人数为29×29=841，故选择B项。

【例题2】同学们排练团体操，排成一个三层空心方阵多出9人，如果在空心部分再增加一层又差7人。问有多少名学生参加了团体操比赛?

A.89 B.93 C.105 D.121

【解析】此题是一个空心方阵的例题，根据排成一个三层空心方阵多出9人，如果在空心部分再增加一层又差7人，可知空心方阵再加的一层共16人，根据规律每层总人数依次增加8可知，原来的三层空心方阵每层认识分别为24人、32人、40人，所以总人数为24+32+40+9=105人，故选择C项。

行程图巧解行程问题

2021公务员考试行测备考正在进行中，下面跟着中公教育走进行程问题，利用行程图巧妙的解答，把行程问题的分值收入囊中。

公式法

若题干等量关系明确，直接求解。即可通过基本公式：路程=速度×时间直接求解。

例题：货车早上8点出发，以60千米/小时的速度匀速驶往40千米外的货场装运货物，装运结束以后以去时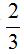的速度匀速返回，并于正午12点到达，那么货车装运货物的时间是其在路上行驶时间的几倍?

A.1 B.1.4 C.1.5 D.1.8

解析：两地相距40千米，去时速度为60千米/小时，可得去时用了40÷60=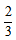小时，回程速度为60×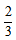=40千米/小时，则回程所用时间为40÷40=1小时，可得货车行驶的总时间为1小时，而总时间为4小时，则装运货物时间为4-1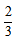=2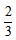小时，因此所求为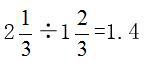倍。选择B选项。

行程图法

若运动过程复杂时，可借助行程图求解。画行程图时利用”路程”建立等量关系。

例1：邮递员骑自行车从邮局到渔村送邮件，平常需要1小时，某天在距离渔村2公里处自行车出现故障，邮递员只好推车步行至渔村，步行速度只有骑车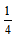的，结果比平时多用22.5分钟，问邮局到渔村的距离是多少公里?

A.16 B.17 C.18 D.19

解析：设平常邮递员骑车的速度为v公里/小时，t小时时自行车出现故障，22.5分钟=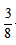小时，结合题意作图如下，

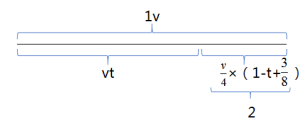
根据图中线段关系可得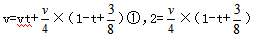,②，由①可得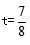，代入②解得 v=16，因此邮局到渔村的距离是16×1=16公里。选择A选项。

例2：甲乙二人上午8点同时从东村骑车到西村去，甲每小时比乙多骑6千米，中午12点甲到达西村后立即返回东村，在距西村15千米处遇到乙，东西两村相距多远?

A.62 B.61 C.60 D.59

中公解析：设甲的速度为v千米/小时，则乙的速度为(v-6)千米/小时，甲到达西村后又走了t小时与乙相遇，结合题意作图如下，

根据图中线段间的关系可得，4v=4×(v-6)+(v-6)t+vt①，vt=15②。解得 t=1，v=15，故东、西两村相距 15×4=60 千米。选择C选项。

各位考生在利用行程图解行程问题时一定要谨记，标注数据时统一标注为“路程”。如果题干中没有直接表述路程的具体数据，可通过路程=速度×时间来表示，遇到未知量可设为未知数，即某段路程可用vt来表示。利用行程图中同段路程相同来建立等量关系，不要惧怕未知数较多，计算时可进行消元。希望各位考生对于行程图法需多加练习，准确无误的选择答案。