政华教育

例1：2015年5月，全国医疗机构出院人数达1738.4万人，同比提高3.0%，环比降低1.1%。其中：医院1330.2万人，同比提高4.6%，环比降低1.1%;基层医疗卫生机构333.4万人，同比降低0.7%，环比降低4.4%;其他机构74.8万人。医院中：公立医院1156.5万人，同比提高3.4%，环比降低1.4%;民营医院173.7万人，同比提高13.7%，环比提高0.7%。

问题：与上年同期相比，2015年5月增长率最高的指标是：

A.全国医疗卫生机构出院人数 B.公立医院出院人数

C.民营医院出院人数 D.基层医疗卫生机构出院人数

【解析】：根据材料数据，可知四个选项的增长率依次为3.0%、3.4%、13.7%、-0.7%，则增长率最高的指标是C项。

例2：2013年全国农民工总量26894万人，比上年增加633万人。其中，外出农民工16610万人，增加274万人;本地农民工10284万人，增加359万人。在外出农民工中，住户中外出农民工13085万人，增加124万人，举家外出农民工3525万人，增加150万人。

问题：与2012年相比，2013年以下四项增长率最低的是：

A.农民工总量 B.外出农民工

C.住户中外出农民工 D.举家外出农民工

【解析】：

与2012年相比，2013年农民工总量增长率为

住户中外出农民工增长率为可知住户中外出农民工增长率最低，选择C。

以上题目重点是对增长率常见的三种比较类型问题进行举例说明，在做题的过程中，需要掌握核心公式进行深入理解，结合简单计算进行比较，多加练习，扎实基础，从而能做到熟练应用。

深入浅出探究“等差数列”

对于大多数公考考生来说，行测数量关系一直是一个令人头疼的板块，虽然在数量关系中确实有一部分题目有一定的难度，解题的过程可能也会花比较多的时间，但是并不是意味着数量关系中所有的题目都特别难，还是存在有部分题目比较简单,而且还具备一定的技巧;对于这部分题目，如果我们掌握了相应的解题策略，也可以很快的对这部分题目进行求解。今天就重点学习在行测数量关系中具备固定解题策略的一类问题——等差数列。

一、定义

等差数列是指从第二项起，每一项与它的前一项的差等于同一个常数的一种数列。

二、核心公式

三、例题展示

【例题1】如果一个等差数列共有25项，和为3700，而且它的每一项都是自然数，那么这个等差数列的第13项的值是多少?

A.74 B.8 C.148 D.160

【解析】C。由等差数列求和公式可知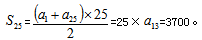，解得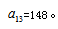。故本题选C。

【例题2】论文集中收录了一篇十多页的论文，其所在各页的所有页码之和为1023。问这篇论文之后的一篇论文是从第几页开始的?

A.94 B.99 C.102 D.109

【解析】B。结合选项且论文有十多页，根据等差数列中项求和公式，1023÷11=93，则这篇论文最后一页页码为98，本题所求为99。故本题选B。

【例题3】某剧院有33排座位，后一排比前一排多3个座位，最后一排有135个座位。这个剧院一共有( )个座位。

A.2784 B.2871 C.2820 D.2697

【解析】B。等差数列求和问题，公差为3，则第一排有135 -(33-1)×3=39个座位，座位总数为33×(39+135)÷2=2871个。故本题选B。

总结：通过上面的讲解，相信大家对于等差数列的解题策略，已经有了更深入的认识，同时也希望同学们后续多加练习，从而达到快速掌握，为后期解决类似题目奠定基础的目的。

三步巧解“牛吃草”问题

在行测数量关系考试当中，我们会经常见到一种利用动物去进行切入的数学问题——牛吃草模型。它是牛顿研究的一种纯粹数学理论模型。这一类题型它暗含的条件是牛每天吃草量是不变的，草生长的速度也是不变的。然后他求的问题是牛吃多少天才能把草吃完这样一个问题。通过一道例题来说明：

【例1】牧场上有一片青草，每天都生长得一样快。这片青草供给10头牛吃，可以吃22天;供给16头牛吃，可以吃10天。期间一直有草生长且生长速度不变。如果供给25头牛吃，可以吃多少天?

【解析】题干其实提到了两种不同的方式去吃同一片草地上的草的问题。解决这种问题的步骤是：

1.区分牛(消耗者)和草(补充者);

2.设每头牛每天的吃草量为1，(设效率为几取决于题目当中牛数量的数量级，可以设一头牛每天吃草量为1，也可以设1万头牛每天吃草量为1，根据题目进行调整。)草每天生长的速度为v;

3.根据公式列方程。

这道题本质上是一类追及问题。无论你以哪种方式去追，最原始的追及距离是不变的，也就是原始草量不变。那我们用追及问题的公式：追及路程S=追及两者速度差乘以追及时间，放在这个问题上。

结合以上两条式子，有，得到原有草量为110。问题问25头牛可以吃多少天，我们还能列出一条式子，原有草量所以这一片草地牛去吃的话5.5天能吃完。

那我们再来看一道牛吃草问题的变式题。

【例2】一艘船有一个漏洞，水以均匀的速度进入船内，当发现漏洞时船内已有一些水，现在要派人将水淘出船外，如果派10个人需要4小时淘完;如果派8个人需要6小时淘完。若要求用2小时淘完，需要派多少人?

【解析】这道题描述了用不同的方式去淘水，直至把水淘完这件事情，在这两种方式下原有水量都是一样的。在解题过程当中，区分好消耗者-淘水，补充者-水在不断地涌进来，设一个人每小时淘水量为1，每小时进水量为v，因为问题问若要2小时淘完要派多少人，我们不妨再设所求为x。根据以上我们所学知识可列方程：

联立方程，求，

原有水量为24。根据问题问法，还能列出。也就是要2小时淘完，要派16人。

希望大家这次学完牛吃草问题，以后可以顺利解题!

一题三式

数量关系是行测考试中难度比较大的一部分，许多同学在考试中都是无奈直接放弃这部分题目。其实数量关系并没有我们想象地那么难。要想做好数量关系，最根本的是寻找题目中的等量关系，只要我们能找到题干中的等量关系，然后列出方程或等式，就可以解出大部分的题目。今天，就通过一道题目带领大家理解如何寻找题干中的等量关系，如何一步步列出最简单的方程，迅速得出答案。

例：老张去年在市内购买了A、B两套房产，并分别花费20万元进行装修。如果房产A的购房款占两套房产购房总额的60%，且A房产购房加装修的总花费为B的1.4倍。问：老张去年购买并装修两套房产共花费多少钱?

A.240 B.220 C.200 D.180

正确答案为：A

方程一：

【解析】观察题干，房产A的购房款占两套房产购房总额的60%，“占”字告诉我们这里就存在一个等量关系，我们可以设A、B两套房产购房款分别为X、Y,可以列出方程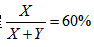;A房产购房加装修的总花费为B的1.4倍,“倍”字提示我们这里存在另外一个等量关系，我们可以列出方程X+20=1.4×(Y+20)。两个方程联立，我们可以解出X=120，Y=80。本题所求为X+Y+20+20=240，答案选B。该种解法通过题干中的两个等量关系，我们设了两个未知数，列了两个方程，求得正确答案。

方程二：

【解析】上面第一种解法，首先解决了我们能不能做出来这道题的问题，但是两个方程，两个未知数解起来，可能需要一些时间，我们能不能只设一个未知数呢?房产A的购房款占两套房产购房总额的60%，我们可以设两套房产购房总额为X，那么A的购房款就是0.6X，B的购房款就是0.4X。A房产购房加装修的总花费为B的1.4倍,我们可以据此列出方程0.6X+20=1.4×(0.4X+20),解得X=200。本题所求为X+20+20=240。这种方程解法相比第一种方程列法的好处在于：不用设置过多的未知数，根据题目中第一个等量关系设好未知数，根据第二个等量关系列出一个方程，然后求出正确答案。

方程三：

【解析】这道题我们还能不能列出其他的方程呢?房产A的购房款占两套房产购房总额的60%，相当于A的购房款：两套房产购房总额=3：5，也就是A的购房款如果为3份，那么B的购房款为2份，我们设A、B的购房款分别为3X、2X，据此列出方程3X+20=1.4×(2X+20),解得X=40，所求为5X+20+20=240。

这种方程列法相比第二种列法，它的特殊性在于根据题干中的比例关系，结合份数思想设出未知数，然后迅速列出方程得出答案。

通过上面三种列方程的方法，大家会发现，其实做好数量关系并不难，首先最重要的是找出等量关系，在此基础上尽可能列出最简便的方程，即使不能列出最简便的方程，我们也也可以按照第一种最基本的方法列出方程，求出答案。做好数量关系的根本，是我们要有一双善于发现等量关系的“慧眼”。