政华教育

第二步，“每8人坐一桌，最后多7人”说明实际参赛人数除以8余数为7;“每7人一组，最后多6人”说明实际参赛人数除以7余6。根据余数定理，差同取差，以最小公倍数最为周期，则实际参赛人数为(56n-1)人，且实际参赛人数不足200人，所以n<4，分别代入n=1，2，3，发现只有当n=3时，实际参赛人数为167人，满足“每5人坐一辆车，最后多2人”即除以5余2，所以实际参赛人数为167人，那么未参赛人数为213-167=46人。

第三步，所以未参赛人数所占比重为46/213≈21.6%，在20%—25%之间。因此，选择B选项。

2022国考行测数量关系：利润问题

在公务员考试中，利润问题是常考的题型，也是我们短期内可以提升的题型，但是令我们头疼的是利润问题里往往会出现很多的量，导致我们不容易理清各个量之间的关系，

其实遇到复杂利润问题我们只需要通过表格的方式理清各个量之间的关系，有同学可能疑惑了，这个表格到底怎么列呢?其实很简单，我们读完题干后题干中出现什么量我们就表示出什么量即可，给出数值用数值表示，没有数值直接设未知量。接下来我们通过几个例题来学习一下。

例题1:

一批商品期望获得50%的利润来定价，结果只销掉70%的商品，为尽早销售掉剩下的商品，商店决定打折出售，这样所获得的全部利润是原来所期望利润的82%，问打了几折?

A.4折B.6折C.7折D.8折

答案：D。期望获得50%利润，也就是利润率是50%，设成本为x，定价为1.5x,销掉70%的商品，又提到数量，设总数为y，销掉0.7y，还剩0.3y，商店打折出售，设打折率为n，则打折后的售价为1.5xn，最后一个条件又提到利润，所以还需要表示出利润，以定价出售单件利润为1.5x-x=0.5x，则定价出售的总利润为0.5x×0.7y，打折后的单件利润为1.5xn-x，打折后总利润为(1.5xn-x)×0.3y。最终告诉我们按照所获得的全部利润是原来所期望利润的82%，期望的利润即在所有商品定价下获得的利润，也就是0.5xy。

最终得0.5x0.7y+(1.5xn-x)×0.3y=0.5xyx82%，等号左右两边消掉xy，最终解得n=0.8。打八折，选D项。

例题2:

某品牌代理商2016年以80元/件的价格购进一批毛衫，以200元/件的价格卖出。2017年受市场环境影响，毛衫的进价上涨了30元，售价不变。2017年毛衫的销量比2016年提高25%，但总利润比2016年少了6万元。那么该代理商2017年销售这种毛衫共获利多少万元?

A.64 B.90 C.160 D.210

答案：B。设2016年毛衫销量为x，2017年为1.25x。

120x-90×1.25x=6，解得x=0.8万件。所求为90×1.25×0.8=90万元。

2022国考行测数量关系：最值问题

行测考试中数量关系这部分的题目很多同学会很纠结，如果每道题都做，那么整体时间会不够;如果一道题都不做，只靠“感觉”去蒙，那么又会影响到行测考试的整体分数。所以，我们一般会建议大家用10分钟的时间去挑3-4道，再根据做出来的选项去“蒙”，正确率会高很多。那么，在这有限的10分钟里我们要挑什么什么样的题做呢?

1.什么是和定最值

和定最值，顾名思义，在和一定的条件下求解最值的问题。让我们来通过一道例题，来看看和定最值的题型特征。

例题：在一场百分制的考试中，5个人的总分是330分，这5个人都及格了，而且每个人成绩是互不相等的整数。那么成绩最好的最多得几分?

首先我们去看题干，“5个人的总分是330分”意思是这5个人的成绩和是一个定值，也就是“和定”，问的是“成绩最好的最多得几分”求得是其中一个人所得成绩最大值，也就是“最值”，属于和定最值的题型特征。

2.解题原则

对于和定最值问题的解题原则是：当总和一定的情况下，若要求其中某个量的最大值，其他量应该尽可能小，若要求其中某个量的最小值，其他量应该尽可能大。解题方法主要就是设未知数，根据题目列方程求解。

3.方法运用

例题：在一场百分制的考试中，5个人的总分是330分，这5个人都及格了，而且每个人成绩是互不相等的整数。

问题1：成绩最好的最多得几分?

题目中提到每个人是互不相等的整数，所以我们可以将5人成绩按照从大到小进行排序。根据解题原则，5人成绩总和是330，成绩最好的人得分要尽可能地多，那其余4人得分要尽可能小，而且每个人都及格且是互不相等的整数，进而可以推出第五名成绩为60，第四名成绩要比第五名多，还得尽可能小，那么就比第五名多1分，也就是61，以此类推，第三名成绩为62，第二名成绩为63。设第一名成绩为X，可列方程：X+63+62+61+60=330，解得X=84，因此成绩最好的最多得84分。

问题2：成绩最差的最多得几分?

依然将5人成绩按照从大到小进行排序。根据解题原则，5人成绩总和是330，成绩最差的人得分要尽可能地多，那其余4人得分要尽可能小，而且每个人都及格且是互不相等的整数，我们会发现成绩好的人分数要尽可能的低，成绩差的人成绩反而要尽可能的高，每个人都不好确定，那不妨就问谁设谁，设第五名最多为X，那么第四名成绩要比第五名高，要尽可能的低，还得是整数，那么就比第五名多1分，也就是X+1，以此类推，第三名成绩为X+2，第二名成绩为X+3,第一名成绩为X+4，可列方程：X+4+X+3+X+2+X+1+X=330，也就是5X+10=330,解得X=64，因此成绩最差的最多得64分。

问题3：若第一名成绩不超过70，则成绩第三的最少得几分?

同样的条件下，依旧将5人成绩按照从大到小进行排序。根据解题原则，5人成绩总和是330，成绩第三的人得分要尽可能地少，那其余4人得分要尽可能多，而且每个人都及格且是互不相等的整数，我们可以先把能够确定的先确定下来。第一名要尽可能地多，而且不超过70，那么第一名最多就是70分，第二名要比第一名分少，还得是尽可能的大的整数，那么第二名就比第一名少1分，也就是69，第三名是我们要求的，不妨设第三名最少为X，那么第四名成绩要比第三名低，还得是尽可能高的整数，那么就比第三名少1分，也就是X-1，以此类推，第五名成绩为X-2，可列方程：70+69+X+X-1+X-2=330，解得X≈64.67，因为每个人都是整数，这里的X是第三名最少的得分情况，第三名最少是64.67，分数不能比64.67更少，所以需要向上取整为65分。

以上就是对和定最值基础题型的一些分析，大家掌握好解题原则之后，多多练习，和定最值将会是帮助我们得分的一类问题。

2022国考数量关系答题技巧：发散思维

行测数量关系中，很多题目并不是中规中矩的，考生在做题的时候要学会发散思维，让我们的大脑活跃起来，跳出题目本身来加强学习。下面我们一起通过学习来实际体验一下。

例1：有135人参加某单位的招聘，31人有英语证书和普通话证书，37人有英语证书和计算机证书，16人有普通话证书和计算机证书，其中一部分人有三种证书，而一部分人则只有一种证书。该单位要求必须至少有两种上述证书的应聘者才有资格参加面试。问至少有多少人不能参加面试?

A.51 B.50 C.53 D.52

从问题“如何才能让不能参加面试的人尽量少”入手，不能参加的要少，就要让能参加面试的人尽量多。有2种证书或3种证书的人能面试，即让这类人要尽量多。(2)结合集合图可知，在31、37和16个分别拥有2种证书的人中，都包含拥有3种证书的人，设有3种证书的为x人，有2种证书或3种证书的人=31-x+37-x+16-x+x=84-2x。(3)依题可知，应让84-2x尽量多，即只能让x尽量小，最小为1，有2种证书及以上的人数最多有84-2*1=82人。135人中有82人有两种及以上证书，剩下的135-82=53人都只拥有1种证书，无法参加面试——>答案是53。故答案为C。

【思维跳跳糖】今天，让我们打开脑洞，学会应该怎样分析，才能让逻辑思维稍微弱点的小伙伴们也能理解这类考题呢?我们就来反向地理解一下原理吧!举个例子：现在在玩游戏，现在桌上有雪碧、可乐、龙井各一杯，只要完成“3分钟喝完任两杯”任务，即被授予“饮神”称号。小明爆发洪荒之力，3分钟喝完3杯;小王只能喝完雪碧和可乐;小李喝完了可乐和龙井各一杯;另10个小伙伴均只喝完1杯。那么，能获得“饮神”称号的有几人?(显然，答案是3。)如果，题目变型：3分钟内能喝完雪碧和可乐的有2人;能喝完可乐和龙井的有2人;3杯全能喝完的只有小明。请问，实际是几人能获得“饮神”称号?答案：2-1+2-1+1=3人。分析：由于“3分钟内喝完雪碧和可乐的2人”中包含小明，“能喝完可乐和龙井的2人”中也有小明，所以计算时注意减去小明，并且，最后不忘加上小明这个符合要求的人。答案应当是：2-1+2-1+1=3人。那么，今天这道题目的解析中，提到的：“有2种证书或3种证书的人=31-x+37-x+16-x+x=84-2x”。

行测数量关系：“不亏钱”原则解决空瓶换水问题

近年来公务员考试行测中的数量关系部分考察形式越来越灵活了，很多考生不仅要学习各类题型和方法，又要学会分析题目条件，备考期间常常会感觉无从下手。所以很多同学比较喜欢学到一些通用的方法来解决同一类题目，给大家介绍这样的一个小窍门——“不亏钱”原则解决空瓶换水问题。

一、什么是空瓶换水问题

若题目中出现x个空瓶可以兑换y(一般为1)瓶水或饮料的规则时，这类题目就称之为空瓶换水问题。例如：

某便利店销售每瓶1元的矿泉水，老板举办活动5个空瓶可换1瓶矿泉水，问小明用100元最多可以喝到多少瓶水?

A.120 B.123 C.124 D.125

二、难点及原则

上题中很容易犯的错误是100元购买100瓶水喝完后，100个空瓶按照每5个换1瓶水计算，100÷5=20，错选为A，但题目要求是最多可以喝到多少水，发现换到手的20瓶水喝完，就又有了20个空瓶，此时可以继续兑换出20÷5=4瓶水，再喝完得到4个空瓶，此时不够5个就无法兑换，又错选了C。但是4个空瓶可以向老板借1个瓶子换1瓶水，然后喝完把空瓶再还回去，因此最多实际可以喝到100+20+4+1=125瓶水。其中的难点主要是多次兑换和先借后还两方面。因此，我们可以从最后的结果来分析，发现老板一共收到了100元钱和125个空瓶，而125空瓶相当于25瓶水;此时老板给兑换125瓶水就恰好相等，老板是不亏钱的，即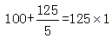那么我们可以得出——可以概括为老板在交易中永远“不亏钱”原则。掌握这个原则还可以解决其他类型的空瓶换水问题。

三、其他考察形式

例1、某便利店销售每瓶1元的矿泉水，老板举办活动15个空瓶可换4瓶矿泉水，问小明用100元最多可以喝到多少瓶水?

A.126 B.130 C.136 D.140

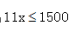【解析】设小明最多喝x瓶水，根据“不亏钱”原则可知，化解后得出即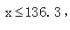x取整为136，选择C。

例2、某便利店销售每瓶1元的矿泉水，老板举办活动5个空瓶可换1瓶矿泉水，某班聚会总共喝了250瓶水，问最少需要花多少钱?

A.200 B.220 C.230 D.240

【解析】设最少需要花x元，根据“不亏钱”原则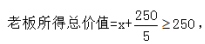，解得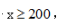则最少需要花200元，选择A。

总的来说，大家在遇到空瓶换水问题时，可以从最后的结果上来判断，根据“不亏钱”原则列出一个不等式，就可以很快得出正确选项。

2022国考行测数量关系：一个公式解决成绩统计问题

统计方法数的题目是公考数量关系当中重要的一个考点，在这类考点中有一类题目只要我们掌握了其中的内涵技巧便可以迅速解出，通过一个例子带大家来认识下成绩统计问题。

例.某次数学竞赛共有6道选择题，评分办法是答对一道得4分，不答得0分，答错一道扣1分。成绩可以有负分，这次竞赛最多有多少种不同的成绩?

A.25 B.26 C.27 D.28

解析：A，这道题给出了数学竞赛的题量和评分办法，让咱们统计成绩的数量，这类题目咱们就可以称之为成绩统计问题，做这一类题目如果咱们直接去分类求解的话太过繁琐麻烦，在这儿教大家一个公式可以解决这类题目，所求数目=总数-取不到成绩数，用字母表示为nm+1-[(m-2)+(m-3)+…+1]，其中n为题目数，m为单题最大分值与最小分值的差。

从题目中咱们可以知道：n=6，m=4-(-1)=5，所以m-2=5-2=3，代入公式所求为6×5+1-(3+2+1)=25，故选择A项。

通过这个公式大家会发现求解这一类题目轻松多了，所以记公式也是学习的一种不错的途径，那怎么快速记忆这个公式呢，咱们来总结一个口诀：积+1-和。为了进一步提升做题速度，咱们来梳理下做这类题目的步骤：

第一步，确定n、m、m-2的值;

第二步，代入公式计算。

我们通过一道题目来检验一下，看大家是否真的掌握了。

【练习】某测验包含10道选择题，评分标准为答对得3分，答错扣1分，不答得0分，且分数可以为负数。如所有参加测验的人得分都不相同，问最多有多少名测验对象?

A.38 B.39 C.40 D.41

解析：答案A，这是2018年浙江公务员考试的一道考题，让我们求的是测验对象最多有多少名，由于所有参加测验的人得分都不相同，所以求测验对象最多有多少名实际上就是让我们求得分最多有多少种，符合我们成绩统计问题总计的公式，所以我们按照做题步骤来做一下。

第一步，根据题干可知：n=10，m=3-(-1)=4，m-2=4-2=2;

第二步，代入公式：所求为10×4+1-(2+1)=38，故选择A项。

一个公式解决成绩统计问题，大家只需记住咱们的公式口诀“积+1-和”，熟练应用做题的两个步骤，成绩统计问题就迎刃而解了。