行测备考-数量关系
生活中的统筹之排队取水问题
统筹问题是用数学思维来研究人力、物力的运用和筹划，以便发挥最大效率的一类问题。
统筹问题所包含的内容非常繁杂，比如物资调运、工作分配、排队等。这些都是我们在日常生活、工作中经常碰到的问题，把它们安排得更快、更好、更合理，这就是统筹问题存在的最大意义。
要解决统筹问题，必须掌握统筹方法。所谓统筹方法，就是一种安排工作进程的数学方法，比如效率优先原则就是其中一种。
而在统筹问题中有一类问题很有意思，就是排队取水问题，我们通过几道例题来看一下：
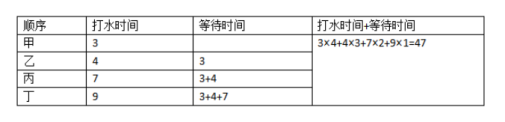
例1：甲、乙、丙、丁去排队打水，4人打水所需的时间分别为3分钟、4分钟、7分钟、9分钟。如果只有一个水龙头，要使甲、乙、丙、丁4人打水的时间与等待的时间之和最短，则这个最短时间是多少?
【解析】要使4人打水的时间与等待的时间和最短，让等待时间最短即可，因为打水的时间是固定的，所以在只有一个水龙头的情况下，肯定是打水时间最短的人先打，打水时间最长的后打，所以，4个人的打水顺序是甲、乙、丙、丁。
变形：
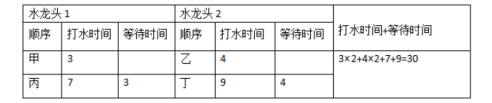
例2：在例1的基础上，把“只有一个水龙头”改为“可以同时使用2个水龙头打水”。
【解析】要使4人打水的时间与等待的时间之和最短，只需让等待时间最短即可，因为打水的时间是固定的，所以在有2个水龙头的情况下，4个人的打水情况如下长:
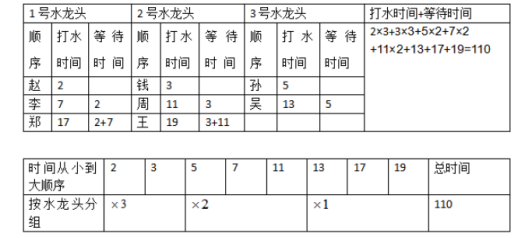
例3：8个人去水房打水，8人打水所需的时间分别为2分钟、3分钟、5分钟、7分钟，11分钟、13分钟、17分钟、19分钟。如果水房只能同时打开3个水龙头，要使8人打水的时间与等待的时间之和最短，则这个最短时间是多少?
【解析】按打水时间从小到大，把这8个人分别叫作:赵、钱、孙、李、周、吴、郑和王。则这8个人的打水情况如下表:
大家发现解题规律了吗?
①按照打水所需时间将时间按从大到小依次排开，
②照从1开始的自然数与排好的顺序依次相乘，具体乘几个数有几个水龙头决定。
同学们理清思路了吗?
行测技巧之行程“不变”应“万变”
行测考试行程题型一直作为考查重点，今天我们来看看考查了很多次的相遇问题，了解下二次相遇中追上也是相遇的奇妙过程，相信通过学习，这类题大家之后肯定能手到擒来!
一、什么是“追上即相遇”
甲、乙两人分别从A、B两地同时出发，相向而行，第一次相遇之后继续前行，到达目的地后都立即返回。
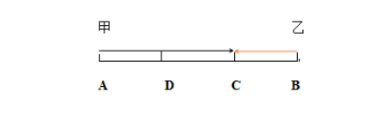
问题1：若甲、乙的速度比为2:1，第二次相遇在哪?
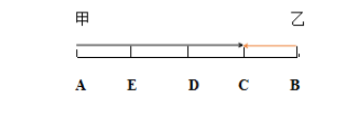
【解析】若甲、乙的速度比为2:1，时间一样，路程比=速度比，则甲乙的路程比也为2:1(如下图)，在C处相遇后继续前行，保持路程比为2:1，则当甲到B地再返回时到达C点，乙应该到达D点;接着继续前行，甲又走2份路程到达A点，此时乙走1份路程也到A点。
问题2：两人速度比继续扩大又会出现什么情况呢?
【解析】若甲、乙的速度比为3:1，时间一样的前提下，路程比依然保持3:1(如下图)：
每当甲走3份路程，乙要走1份路程，则有，当甲返回途中到D时，乙也到D，此时两人方向相同，甲从背后追上了乙，在还没来得及发生第二次迎面相遇时就已经追上了。
问题3：哪些题的二次相遇属于这种情况呢?
【解析】回顾上边两个例子，发现结论：速度比一旦超过2:1，则存在第二次追上即相遇。
二、初识“追上即相遇”
上午9点整，甲从A地出发，骑自行车去B地，乙从B地出发，开车去A地。两人第一次相遇时为9点半，甲、乙到达目的地后都立即返回。若甲、乙的速度比为1∶3，则他们第二次相遇时为：
A.9:40 B.9:50 C.10:00 D.10:10
E.10:20 F.10:30 G.10:40 H.10:50
【解析】已知甲乙速度比1:3，则存在第二次追上即相遇，根据题目描述作行程图如下：
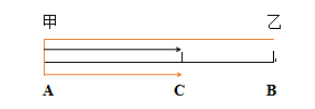
从出发直接到第二次追上(在C处)，由行程图知甲乙的路程差固定为全程AB距离，由追及基本公式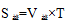
知，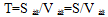
,而全程S是第一次相遇甲乙两人的路程和，从九点出发到九点半第一次相遇，时间是30分钟，所以
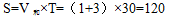。则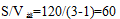
,九点出发，60分钟后第二次追上，故第二次相遇时为10:00。本题选C。
在第二次追上即相遇的题目中，从出发到第二次追上，路程差恒定不变，固定是一个全程，找到这一不变，一切难点迎刃而解!
三、巩固训练
甲、乙二人分别从A、B两地同时出发，相向而行，甲的速度是乙的4倍，甲用时15分钟到达B地后立即返回，甲乙第二次相遇后，乙再走( )分钟才能到达A地。
A.40 B.30 C.45 D.33.3
【解析】速度比4:1，则第二次存在追上即相遇，从出发到第二次追上作行程图如下：
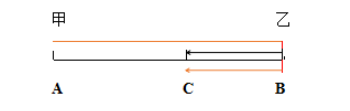
路程差固定为一个全程S，用时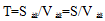
，由于题目已知甲走全程用时15分钟，所以
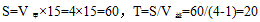,所求时间为乙走全程时间减去20分钟，全程一定，甲乙速度是4:1，时间呈反比，则甲乙时间之比为1:4,1份对应甲走全程的15分钟，故4份对应60分钟，即乙走全程用时60分钟，所求即为60-20=40，本题选A。
以上就是关于相遇问题的解决技巧，相信你已经找到这类题的法宝了，动动手指，勤做练习吧!
均值不等式在极限思维中的运用
同学们对于极限思维这个概念都不陌生，极限思维其实在指用极限状态分析问题和解决问题的一种数学思维，简单来说就是求最大值或者最小值问题。那均值不等式在极限思维中如何体现的呢，这一类型的题型特征是什么呢以及如何掌握它的解题思路，是同学们相对比较关心的内容，让我们一起来学习一下吧。
一、均值不等式的题型特征
均值不等式是属于极值问题中的一个运用，也是可以用极限思维来解题的，一般在题干或者问法中出现最大或最小，最多或最少、至多或至少。
二、均值不等式的定理
均值不等式的定理，若a、b是实数，则a2+b2≧2ab，符号当且仅当a=b的时候取得。一般适用于两种题型，(1)当和一定时，求积的最大值，也就是若a、b均是正实数，则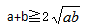
，符号当且仅当a=b的时候取得。但如果两个数a、b取不到相等的时候，和一定的两个数，差越小，积越大。(2)当积一定，求和的最小值，同理，如果两个数a、b取不到相等的时候，积一定的两个数，差越小，和越小。
三、例题展示
例1、若两个自然数的和为20，求这两个自然数积的最大值。
答案为100。解析：根据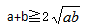
，等号当且仅当a=b的时候取得。可得
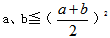，ab要取得最大值仅当a=b的时候取得，所以这两个数分别都是10，他们的积取到最大，且最大值为100。
例2、用60米长的铁板围成一个长方形鸡窝，问这个鸡窝的面积最大是多少?
A、200 B、225 C.300 D、600
答案B。解析：由长方形的周长为60，可知长方形的长加宽的和为60÷2=30，两个数的和一定时，当且仅当这两个数相等时，这两个数的积可取得最大值，也就是长等于宽等于30÷2=15，所以鸡窝的面积最大为长乘以宽等于15×15=225。
