政华教育

1. A是B的n/m。
　　2.抵消型：单独型，即甲先a天，再b天，乙先c天，再d天（讨论a-c与b-d）；合作型：即甲a天完成，甲乙先c天，甲再d天（讨论c+d-a与b-d）。
　　3.效率关系可以是加减，也可以是乘除，比如A是B的2倍；A是B的2/3；A是B的1/5；A比B快35；A比B慢28。
　　【真题演练】

（2016国考）某浇水装置可根据天气阴晴调节浇水量，晴天浇水量为阴雨天的2.5倍。灌满该装置的水箱后，在连续晴天的情况下可为植物自动浇水18天。小李6月1日0:00灌满水箱后，7月1日0:00正好用完。问6月有多少个阴雨天？（）
　 A. 10 B. 16 C. 18 D. 20

【答案】D【解析】由题目所给出的晴天浇水量与阴雨天浇水量之比，可假设晴天浇水量为5，阴雨天浇水量为2，则可得水箱总容量为5×18=90。已知6月整月共有30天，设阴雨天数为a，晴天数为（30-a），则5（30-a）+2a=90，解得a=20天。故正确答案为D。

二、行程问题的比例法怎么使用

数量这类题目难度大，耗费时间多，属于比较能够拉开考生差距的一个模块，复习时也令许多考生望而生畏。你在备考过程中遇到了哪些问题？看看以下问题是否你也有疑惑。
　　比例行程在行程问题中属于比较难的一种小题型。如考生发现题目无法直接使用公式，也不是经典的相遇追及、流水行船等模型时，即可考虑比例行程。

　　使用前，先明确哪个量一定。时间一定，则路程与速度成正比；速度一定，则路程与时间成正比。这两种情况通常比较容易想到，相关题目也比较简单。

但大多数比例行程考查的是路程一定，速度与时间成反比。难点在于，题干往往不会直接说明路程一定，需要考生自己分析和理解条件，必要时还得配合行程图去找哪一段路程是不变的。总之比例行程的出题风格一般是非套路化的，更为灵活多变，侧重考生思维能力的考查。
　　【知识点】
　　比例法是解决行程问题的常用方法，熟练掌握可有效提高做题速度及正确率。行程问题中的核心公式为路程=速度×时间，当其中某个量为定值时，其他两个量成比例关系，此时可考虑使用比例，将比例转化为份数或通过比例列方程。
　　题型特征：
　　行程问题中，只给其中一个量。比如：走同一段路，或时间一定。
　　解题思路：
　　①路程一定，速度与时间成反比；
　　②时间一定，路程与速度成正比；
　　③速度一定，路程与时间成正比。
　　【真题示例】

（2016联考）A、B两辆列车早上8点同时从甲地出发驶向乙地，途中A、B两列车分别停了10分钟和20分钟，最后A车于早上9点50分，B车于早上10点到达目的地。问两车平均速度之比为多少？（）
A.1：1　　 B.3：4　　 C.5：6　　D.9：11
【答案】A【解析】A、B两车均为8:00出发，到达的时间分别为9：50和10：00，中途分别停了10分钟和20分钟，因为两车所用的时间均为1小时40分钟，行驶路程也相同，故二者平均速度之比为1:1。故正确答案为A。

三、如何学习数字推理

所谓数字推理，就是给应试者一个数列，但其中至少缺少一项，要求应试者仔细观察数列的排列规律，然后从四个选项中选出你认为最为合理的一项来填补空白项。解答数字推理题时，应试者的反应不仅要快，而且要掌握恰当的方法和技巧，数字推理规律主要有：等差数列、和数列、倍数数列、乘积数列、多次方数列、分式数列、组合数列等。

　　要想学好数字推理，我们需要积累2个敏感，数字敏感和数列敏感。

　　(一)数字敏感

　　所谓数字敏感指的是我们见到数字后的发散性思维。当我们看到一个数时，能够下意识的联想到一些特殊数或者找到数本身的属性或者是其他的表达形式。对与特殊数字临近的数字要产生联想，比如看到数字7,7可以联想成：7=23-1=32-2.要想真正地培养出对数字的敏感度，还是在于我们平时对于一些特殊数字的积累。主要是一些多次方数：

　　(1)1～21的二次方

　　11²=121 12²=144 13²=169 14²=196 15²=225

　　16²=256 17²=289 18²=324 19²=361 21²=441

　　(2)1～11的三次方

　　2³=8 3³=27 4³=64 5³=125 6³=216

　　7³=343 8³=512 9³=729 10³=1000 11³=1331

　　(3)2的1～10次方

　　2⁴=16 2⁵=32 2⁶=64 2⁷=128 2⁸=256 2⁹=512 2¹⁰=1024

　　(4)1～5的1至5次方

　　3²=9 3³=27 3⁴=81 3⁵=243

　　4²=16 4³=64 4⁴=256 4⁵=1024

　　5²=25 5³=125 5⁴=625 5⁵=3125

　　(二)数列敏感

　　所谓的数列敏感，指的是我们考试的时候，考题的题干往往是以一个不完整的数列给出的，所以这时候当我们看到一个数列时，我们要在脑海里快速地反映出常考的相关相近数列，这样能够帮助我们分析确定考查的是哪一类型数列或数列变式，从而根据我们给大家总结的数列规律来快速解题。数字推理主要考查的数列类型有：等差数列、和数列、倍数数列、乘积数列、多次方数列、分式数列、组合数列等。

　　1.等差数列

　　等差数列题型特征：数列一般单调递增，相邻两数字变化不大(相差1~3倍)，常常给出5个及以上数。

　　等差数列解题方法：逐差法(一次或多次)。

【例1】2,6，12，20，30，( )

【答案】42【解析】先观察，由于给出的数列相邻数字之间变化幅度不大且呈现出单调性，因此我们考虑是否考查的是等差数列，接下来我们就去逐差，经过一次逐差后，我们发现新形成的数列为4,6,8,10，(12)是一个偶数列，因此此题的答案为30+12=(42)。

　　2.和数列

　　和数列题型特征：数列一般前几个数为小数字且相邻数字之间变化幅度不大。

　　和数列解题方法：相邻两项或三项相加得到后项找出规律。

【例2】-1,2,0,4,4，( )

【答案】12【解析】先观察，相邻数字之间变化幅度不大，可以优先考虑逐差或加和，我们经过试错会发现，这个题目考的是和数列，将相邻两项相加可以得到一个新数列：1,2,4,8(16)，是一个公比为2的等比数列。因此括号里应该填16-4=(12)。

　　3.倍数数列

　　倍数数列题型特征：大部分呈单调，变化幅度稍大。

　　倍数数列解题方法：先看大数规律。

【例3】2,14,84,420,1680，( )

【答案】5040【解析】先观察，我们会发现整体变化幅度还是比较大的，所以这种情况下我们一般不考虑逐差或加和，我们会发现1680和前面的420刚好是4倍的关系，往前再推，420与84是5倍的关系，因此此题我们将相邻两项用后一项除以前一项，可以得到一个新数列：7,6,5,4，(3)，这是一个首项为7，公差等于-1的等差数列，因此括号里应填的是1680×3=(5040)。

　　4.乘积数列

　　乘积数列题型特征：大部分呈单调，变化幅度较大。

　　乘积数列解题方法：将相邻两项或三项乘积之后再找规律。

【例4】4,3,10,27,265，( )

【答案】7148【解析】先观察，我们会发现此题既不是考查等差数列、和数列，也不是倍数数列，我们通过观察会发现10,27,265这三个数存在10×27-5=265这样的一个乘积关系，往前推，3,10,27这三个数存在3×10-3=27，依次往前推，我们会发现此题的规律是从第三项开始，每一项=前面两项之积-质数列。因此括号里要填的是27×265-7=(7148)。

　　除了上述四种常考的考点外还有多次方，分式，组合数列等等。

四、数列构造最值问题的解题思路

最值问题是数量关系中非常重要的一种题型，考察频率很高。今天与大家一起探讨一下最值问题中常见的构造数列类题型的解题方法。
　　构造数列类最值问题是最值问题中难度较高的一种题型。主要表现在两个方面，一是在梳理解题思路中，对各个名次的要求需要分析清楚，是应该尽可能高还是应该尽可能低；二是部分构造数列类最值问题计算难度较高，那么在计算时我们就应该尽量结合一些计算技巧，例如尾数法或者相关公式，以提高计算速度。下面通过几道例子详细梳理一下构造类最值问题解题方法的三个步骤如何应用。
　　题型特征：最多(少)的…至多(少)…;排名第N的至多(少)……
　　解题方法：1.排序定位(求谁设谁);2.构造数列(反向推其他);3.加和求解。
例1. 【2014国考】某连锁企业在10个城市共有100家专卖店，每个城市的专卖店数量都不同。如果专卖店数量排名第5多的城市有12家专卖店，那么专卖店数量排名最后的城市，最多有几家专卖店：（）
　　A. 2 B. 3 C. 4 D. 5
【答案】C【解析】设专卖店数量排名最后的城市有x家专卖店。要求专卖店数量排名最后的城市专卖店的数量最多,则令其他城市专卖店数量最少。题目中已知排名第 5 多城市有 12家专卖店，且每个城市专卖店数量不同,则可得下表:

　　根据该企业共有100家专卖店的条件，则有16+15+14+13+12+x+4+x+3+x+2+x+1+x=100，解得x=4，故正确答案为C。
　　【点评】本题在解题过程中“构造数列”时，需要注意题干已经给定第五名的城市有12家专卖店，不能忽略掉这一条件，若将第五名构造成“x+5”进行后续计算，结果会出现偏差。提醒大家，在构造数列的过程中，一定要注意题干是否有特定条件。
例2. 【2018国考】某新能源汽车企业计划在A、B、C、D四个城市建设72个充电站，其中在B市建设的充电站数量占总数的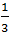，在C市建设的充电站数量比A市多6个，在D市建设的充电站数量少于其他任一城市。问至少要在C市建设多少个充电站?（）
　　A. 20　　B. 18　　C. 22　　 D. 21

【答案】D【解析】因为B市建设充电站的数量占总数的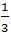，C市又比A市多6个，D市最少，所以四个城市充电站个数关系为：B、C两市建设充电站的数量较多，A市第三多，D市最少。要使C市建设的充电站尽量少，就要让其他市建设的充电站尽量多。其中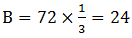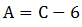，，D尽量多且比A少，所以D最多为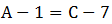。此时充电站总个数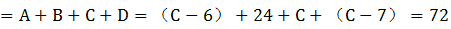，解得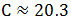，问至少，应向上取整，所以C至少建设21个充电站。故正确答案为D。

　　【点评】在部分构造类最值问题中，解出的答案并非为整数，此时切不可盲目的进行四舍五入，而要根据题目要求进行取舍，提醒大家可以根据口诀进行记忆：“问最多向下取整，问最少向上取整”。例如，我们解出来至多是14.5，那么就不能超过14，此时向下取整，14才是符合要求的答案。
例3.某机关20人参加百分制的普法考试，及格线为60分，20人的平均成绩为88分，及格率为95%。所有人得分均为整数，且彼此得分不同。问成绩排名第十的人最低考了多少分：（）
　　A. 88　　B. 89　　C. 90　　D. 91
【答案】B【解析】

　　如表所示，设排名第十的人考了x分，要想让x尽可能低，其他应尽可能高。因每人得分不同，则1-9名最高可为100-92分。同时，不及格人数=20×5%=1人，不及格的人最高只能为59分。11-19名也应尽可能高，设分别比第十名低了1-9分。前9名与倒数第1名的的总分数=96×9+59=923，则第10-19名的总分数=88×20-923=837。即x+(x-1)+…+(x-9)=837，10x-45=837，解得x=88.2分。问最少向上取整，至少为89分，B项满足。故正确答案为B。
　　【点评】此题有两个特点，第一涉及的名次较多，共有20人，如果20个名次全部构造出来则过于浪费时间，故在解题过程中，分数相连的名次可以列为一格。第二计算量较大，涉及到等差数列的求和以及多位数的加减法。建议考生们在解题过程中一定要掌握相应的计算技巧，在此我们利用等差数列的中位数进行求和便会大大提高我们的计算速度。
例4.【2013国考】某单位2011年招聘了65名毕业生，拟分配到该单位的7个不同部门，假设行政部门分得的毕业生人数比其他部门都多，问行政部门分得的毕业生人数至少为多少名：（）
　　A.10 　　B.11　　C.12　　 D.13
【答案】B【解析】要使行政部门少，则其他部门应尽量多，设行政部门分得x名，其他部门均分得(x-1)名，可列式为x+6(x-1)=65，解得x≈10.1,问最少向上取整，行政部门至少分得11名，故正确答案为B。
　　【点评】在本题中，为什么其他部门分得人数都可以设为(x-1)呢?因为题目中没有说明“各个部门人数均不相同”。所以提醒大家记住，如果题干没说均不相等，则可默认相等。
　　以上就是对于数列构造最值问题的详细讲解。本类题型有一定难度但套路性较强，需要去构造名次及计算复杂方程。在构造名次时，若涉及的名次较少，可以不需画出表格，而较为复杂的推荐画出表格，如此解题会更加清晰。提醒大家记住万变不离其宗，只要知识点掌握牢固、能够融会贯通，无论如何创新如何结合，我们都可以熟练解决，当然这还需要建立在大量练习的基础上。