
行测数量关系考点
容斥问题知识点储备
一、考情分析
容斥问题在最近几年的国家公务员考试中出现的频率逐渐增大,尤其是最近两年都有出现。难度也逐渐增大,不再拘泥于最常规的两个集合和三个集合的考查方式。在各省市的公务员考试中,容斥问题仍然出现活跃。因此,这一题型还是需要重点关注。
二、基本概念
涉及多个相互关联的集合,要求根据集合间的相互关系计算集合中元素个数的问题称为“容斥原理”问题。
三、技巧方法
(一)公式法解两个集合容斥问题
两个集合的容斥问题公式:
A∪B=A+B-A∩B
三个集合的容斥问题公式:
A∪B∪C=A+B+C-A∩B-B∩C-C∩A+A∩B∩C
(二)文氏图法解两个集合容斥问题
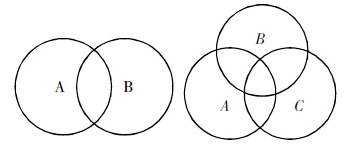
四、例题精讲
例题1:某班有56人,每人至少参加一个兴趣小组,参加生物组的有46人,参加科技组的有28人,两组都参加的有多少人?( )
A.10 B.18 C.24 D.30
【答案】B【解析】集合A={参加生物组的人}、集合B={参加科技组的人},由A∪B=A+B-A∩B知两组都参加的有A∩B=46+28-56=18人。故正确答案为B。
例题2:某单位有青年员工85人,其中68人会骑自行车,62人会游泳,既不会骑车又不会游泳的有12人,则既会骑车又会游泳的有多少人?( )
A.57 B.73 C.130 D.69
【答案】A【解析】我们来用集合Ⅰ表示所有的青年员工,A表示会骑自行车的人,B表示会游泳的人,则A∩B表示既会骑车又会游泳的人,现在设A∩B=x,把题中的数据一一填到表格里面,可以得到:
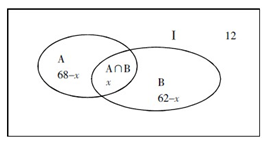
直接计算可以知道,68-x+x+62-x+12=85,因此x=57。故正确答案为A。
例题3:某专业有学生50人,现开设有甲、乙、丙三门选修课。有40人选修甲课程,36人选修乙课程,30人选修丙课程,兼选甲、乙两门课程的有28人,兼选甲、丙两门课程的有26人,兼选乙、丙两门课程的有24人,甲、乙、丙三门课程均选的有20人,问三门课程均未选的有多少人?( )
A.1人 B.2人 C.3人 D.4人
【答案】B【解析】三个集合的容斥原理问题。至少选了一门课的有40+36+30-28-26-24+20=48人,所以三门都没选的有50-48=2人。故正确答案为B。
例题4:某班参加体育活动的学生有25人,参加音乐活动的有26人,参加美术活动的有24人,同时参加体育、音乐活动的有16人,同时参加音乐、美术活动的有15人,同时参加美术、体育活动的有14人,三种活动都参加的有5人,这个班共有多少名学生参加活动?( )
A.36 B.35 C.30 D.25
【答案】B【解析】设A={参加体育活动}、B={参加音乐活动}、C={参加美术活动}
根据题意,将所给的条件填入相应的集合中,可画出文氏图如下:
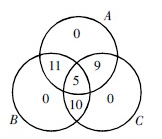
根据图示,可知全班共有11+5+9+10=35名学生参加活动。故正确答案为B。
例题5:某高校对一些学生进行问卷调查。在接受调查的学生中,准备参加注册会计师考试的有63人,准备参加英语六级考试的有89人,准备参加计算机考试的有47人,三种考试都准备参加的有24人,准备选择两种考试参加的有46人,不参加其中任何一种考试的有15人。问接受调查的学生共有多少人?( )
A.120 B.144 C.177 D.192
【答案】A【解析】利用图示法解题。

图中,黑色部分是准备参加两种考试的学生,灰色部分是准备参加三种考试的学生。计算总人数时,黑色部分重复计算了一次,灰色部分重复计算了两次,所以接受调查的学生共有63+89+47-24×2-46+15=120人。故正确答案为A。
浓度问题知识点储备
一、考情分析
浓度问题对多数考生来说相对简单,也是行测考试中的常考题型。只要掌握了浓度问题的公式,弄清楚溶质与溶剂的变化,正确答题还是相对容易的。但是要想快速解题,就需要多加练习,熟练运用解决浓度问题的各种方法,即方程法、特值法以及十字交叉法的应用。
二、基本概念和公式
溶液就是把某种固体或者液体放入水里面,两者混在一起的产物。溶质就是放进去的那种固体或者液体,溶剂就是水。
浓度就是溶质占到整个溶液的百分比。
三、技巧方法
浓度=溶质÷溶液
溶液问题常见的有两种,一种是溶液的混合,这种问题用公式解决;另外一种是单一溶 液的蒸发或稀释,这种题目一般用比例法解决,即利用溶质不变进行求解。
混合溶液特性:一种高浓度的溶液A和一种低浓度的同种溶液C混合后得到溶液B,那么溶液B的浓度肯定介于溶液A和溶液C的浓度之间。
(一)方程法
方程法适用于大部分浓度问题,具有思维过程简单的特点。一般来说,方程法有两个要素,第一是设未知数,要求易于求解;第二是找等量关系列出方程。浓度问题中往往以浓度作为未知变量,这样等量关系易于表达,但也伴有浓度数值大部分是小数不好计算的弊病,还需要在实际做题中细加体会。
(二)特值法
对于那些比例非常明确的浓度问题,我们可以用特值法来避免分数的出现,从而简化计算步骤。
(三)十字交叉法
对于两种溶液混合的结果:某一溶液相对于混合后溶液,溶质增加;另一种溶液相对于混合后溶液,溶质减少。由于总溶质不变,因此增加的溶质等于减少的溶质,这就是十字交叉法的原理。
四、例题精讲
例题1:一杯含盐15%的盐水200克,要使盐水含盐20%,应加盐多少克?( )
A.12.5 B.10 C.5.5 D.5
【答案】A【解析】设应加盐x克,则(200×15%+x)÷(200+x)=20%,解得x=12.5。
例题2:两个相同的瓶子装满某种化学溶液,一个瓶子中溶质与水的体积比是3∶1,另一个瓶子中溶质与水的体积比是4∶1,若把两瓶化学溶液混合,则混合后的溶质和水的体积之比是:( )
A.31∶9 B.7∶2 C.31∶40 D.20∶11
【答案】A【解析】1+3=4和1+4=5的最小公倍数为4×5=20,且3∶1=15∶5,4∶1=16∶4,设瓶子的容积为20,则混合后溶质和水的体积比为(15+16)∶(5+4)=31∶9。故正确答案为A。
例题3:甲杯中有浓度为17%的溶液400克,乙杯中有浓度为23%的同种溶液600克,现在从甲、乙取出相同质量的溶液,把甲杯取出的倒入乙杯中,把乙杯取出的倒入甲杯中,使甲、乙两杯溶液的浓度相同,问现在两杯溶液浓度是多少?( )
A.20% B.20.6% C.21.2% D.21.4%
【答案】B【解析】设混合后总浓度为x。
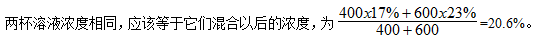
故正确答案为B。
例题4:15克盐放入135克水中,放置一段时间后,盐水重量变为100克,这时盐水的浓度是多少?浓度比原来提高了百分之几?( )
A.75%,12.5% B.25%,12.5% C.15%,50% D.50%,62.5%
【答案】C【解析】原来的浓度是15÷(135+15)×100%=10%。水蒸发以后,盐的质量没变,这时盐水的浓度是15÷100×100%=15%,浓度比原来提高了(15%-10%)÷10%=50%。故正确答案为C。
例题5:一杯糖水,第一次加入一定量的水后,糖水的含糖百分比变为15%;第二次又加入同样多的水,糖水的含糖百分比变为12%;第三次再加入同样多的水,糖水的含糖百分比将变为多少?( )
A.8% B.9% C.10% D.11%
【答案】C【解析】设第一次加水后糖水总量为100,糖为100×15%=15,则第二次加水后糖水总量变为15÷12%=125,所以每次加入的水为125-100=25,故第三次加水后糖水的含糖百分比为15÷(125+25)=10%。
例题6:甲容器中有浓度为4%的盐水150克,乙容器中有某种浓度的盐水若干,从乙中取出450克盐水,放入甲中混合成浓度为8.2%的盐水,那么乙容器中的浓度是多少?( )
A.9% B.10% C.12% D.9.6%
【答案】D【解析】运用十字交叉法。设乙容器内溶液浓度为X
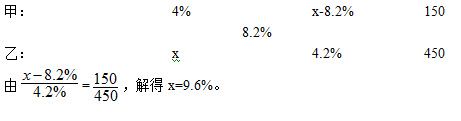
故正确答案为D。








