巧用画图解决数学问题
行测职业能力测验所涉及的题型中，大家公认的比较难的题型就是数量关系，而数量关系主要以数学运算为主，考察各类数学题型，解决数学问题需要借助一些数学工具，比如直尺、圆规、三角板……，当然图形也是我们可以借助的一种“工具”。今天带大家一起感受一下图形的魅力。
一、“画图”之巧记数学公式
数学里包含很多的数学公式，有些数学公式可以借助图形的形式帮助记忆，既形象又直观。
利用图形理解和记忆a²-b²=（a+b）（a-b）
【解析】：如下图1，我们可以把a²看成是边长为a的正方形的面积，b²看成是边长为b的正方形的面积,则a²-b²是图中阴影部分的面积(如图2)，把阴影部分拆成上下两个部分，再把上面的部分移动到下面(如图3),此时阴影部分面积为小矩形的面积等于长×宽：(a+b)(a-b)。
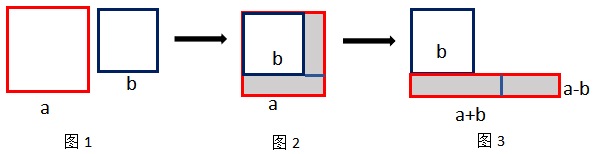
像这样可以利用图形进行理解和记忆的数学公式很多，运用图形就会把原有较为枯燥的数学公式记忆变的更加生动活泼，是不是简单很多?
二、“画图”之化繁为简
众多数学模型里，行程问题成为最大的“拦路虎”，要想解决好行程问题，关键是理解题干所给出的信息，而画图可以更加直观的展现题干信息。有些行程问题其实就是“纸老虎”，看似题干很长让人不明觉厉，实际上一戳就破，使用的工具就是“图形”。
【例题1】赵骑车去医院看病，父亲在发现小赵忘带医保卡时以60千米/小时的速度开车追上小赵，把医保卡交给他并立即返回。小赵拿到医保卡后又骑了10分钟到达医院，小赵父亲也同时到家。假如小赵从家到医院共用时50分钟，则小赵的速度为多少千米/小时?(假定小赵及其父亲全程都匀速行驶，忽略父子二人交接卡的时间)
A.10 B.12 C.15 D.20
【答案】C【解析】如下图所示，父亲在C点追上小赵，并把医保卡交给小赵，小赵从家到医院全程需50分钟，在把医保卡交给小赵后10分钟，小赵和父亲分别到达医院及家里，故在交接医保卡后，小赵父亲10分钟走完小赵骑车40分钟的路程，两者速度之比为40∶10=4∶1，父亲的速度为60千米/小时，小赵的速度为60÷4=15千米/小时，故正确答案为C。
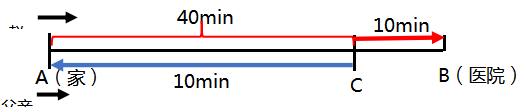
行程本身就是相对较难的题型，如果题干还很长，那么多数考生就会采取放弃的策略，实际上有些题看似题干较长，如果我们能够把文字语言转化到图上，题干信息就会比较直观，可以起到化繁为简的作用。
数学图形的运用，可以帮助大家解决很多的数学问题，合理运用数形结合的思想可以拓宽数学思维，增强解题的技巧。建议大家在日后的备考中要学会使用哦!
教你几招解决年龄问题
年龄问题在国考、省考中也会考到，这类题目的整体难度不大，属于得分题目，只要掌握了基本的计算公式，基本上就可以拿下年龄问题。下面我们一起来学习一下年龄问题。
一、年龄问题解题原则
①两个人之间的年龄差永不变;
②每个人的年龄都会自然增长;
③任何两人年龄之间的倍数关系是变化的。
二、解题方法
①列表格辅助找等量关系;
②通过年龄差等关系进行求解。
三、例题精讲
【例题1】父亲今年44岁，儿子今年16岁，当父亲的年龄是儿子的年龄的8倍时，父子的年龄和是多少?
A.36 B.54 C.99 D.162
【答案】A【解析】方法一：列方程求解：我们设所求当年儿子x岁
根据题干描述可以列表：
我们让x+28=8x可以得出x=4，则8x=32，父子年龄和未4+32=36岁，故正确答案为A。
方法二：根据年龄差不变求解：
父子的年龄差为一个不变量，父子二人的年龄差为44-16=28岁。因此，当父亲的年龄是儿子的8倍时，即两人的年龄差是儿子年龄的7倍，那时儿子的年龄为28÷7=4岁，则父子的年龄和为儿子年龄的(8+1)倍，为4×(8+1)=36岁。故正确答案为A。
【例题2】1998年，小张的年龄是小王的年龄的4倍。2002年，小张的年龄是小王的年龄的3倍。问小张、小王二人2000年的年龄分别是多少岁?
A.34岁，12岁 B.32岁，8岁 C.36岁，12岁 D.34岁，10岁
【答案】D【解析】我们可以设小王1998年为x岁，则可以根据题干列表：
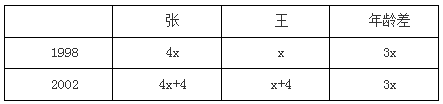
其中4x+4=3×(x+4)可以得出x=8，则2000年小张为4x+2=34岁，小王是x+2=10岁，故正确答案为D。
解开最不利原则的神秘面纱
近年来，国考行测数量关系越来越侧重对极限思维的考察，而在考察的众多题目中，有这么一类题目，特征鲜明，题干出现“至少……才能保证”的描述，这就是我们常说的最不利原则问题。这种问题要想揭开其神秘的面纱，就要充分地发挥想象力，构思“最不利的情况”来解题。今天，我们就特意帮助大家对于这类题目的解题思维进行梳理。
一、题型特征
问法：至少……才能保证
二、解题核心
1.先尽可能让保证的事件不发生
2.保证数=最不利的情况数+1
三、最有利原则和最不利原则区别
为了更好地理解最不利原则问题，我们可以将很容易理解的最有利原则和最不利原则进行对比分析。
1.一副完整的扑克牌，至少抽几张就有可能2张牌点数相同?
2.一副完整的扑克牌，至少抽几张才能保证2张牌点数相同?
第一题，结合问题，要使抽到的牌最少，还能满足2张牌点数一样，直接考虑最幸运的时候，即抽到的第二张牌跟第一张牌点数一样，所以抽2张就可以了。这个我们很容易理解，这就是最有利的情形。
第二题，我们要确保抽到的两张牌点数一样，就必须把这副完整的扑克牌的所有不同的点数都抽出来，即大王、小王以及从1点到13点各一张，共15张牌，然后我再抽出一张牌，无论这一张牌是多少点，一定能够保证2张牌的点数相同，所以至少需要抽16张牌。像这种情况就是最不利情形。
四、例题展示
【例题1】一个盒子里装有红球5个、黄球9个、蓝球12个，每次摸1个球放到盘子里，最少摸几次，才能保证一定有6个是同色的?
A.16 B.17 C.19 D.21
【答案】A【解析】根据题干中“至少……才能保证”判定是最不利原则问题，第一步，找到最不利的情况数，要保证6个颜色相同，红球总数少于6个，需要全摸出来，另外黄球和蓝球各摸5个。第二步，保证数=5+5+5+1=16，故正确答案为A。
【例题2】某单位组织党员参加党史，党风廉政建设，科学发展观和业务能力四项培训，要求每名党员参加且只参加其中的两项。无论如何安排，都有至少5名党员参加的培训完全相同。问该单位至少有多少名党员?
A.17 B.21 C.25 D.29
【答案】C【解析】问法是“无论如何安排，都有至少5名党员参加的培训完全相同。问该单位至少有多少名党员”，但这句话转化一下就是“至少……才能保证5名党员培训完全相同”，所以属于最不利原则问题。首先需要借助排列组合求出党员可供选择的方案，每位党员从4个项目中选择2项共有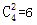
种方案。第一步，找到最不利的情况数，5人培训相同，最坏的情况是这6种培训方案每种都有4个人，即6×4=24，第二步，保证数=24+1=25，故正确答案为C。
通过以上题目的讲解，相信大家对最不利原则这类题目有了比较清晰的认识，在备考过程中，只要大家勤加练习，熟练解题方法和思路，大家再遇到此类题目也便不再畏惧。
最不利原则巧解极值问题
极值问题是行测数量关系考题中常见的一种题型。具体又细分为和定最值和最不利原则两个常考考点。最不利原则的考题问法较为固定，容易区分，我们主要通过以下三个方面来进行学习：一是例题引入帮助我们掌握做题思路;二是整理题型特征和解题原则;三是巩固复习来熟练应用此种解题原则。
一、例题引入
问题一：现有一幅完整的扑克牌，从中至少抽出几张就有可能摸到一张大王?(1张)
问题二：现有一幅完整的扑克牌，从中至少抽出几张就能保证有一张大王?(54张)
解析：对于问题一，更多强调的是一种可能性，即对我们最有利的情况，一张就可能抽到大王;对于问题二，更多强调的是在尽可能少的情况下，必须保证有大王。此时只能考虑对我们最不利的情况为，将其他53张牌抽完，此时再摸一张，一定可以保证是大王。
二、题型特征和解题思路
题型特征：最不利原则并不是一类题型，它是针对某类题型的固定解题原则。此类题型常见问法为：至少……才能保证……。
解题思路：要想保证事件发生，必须考虑对我们最不利的情况，即离成功一线之差的情况，最后再加“1”，总结为：结果数=最不利情况数+“1”。
三、巩固练习
【例题1】一幅完整的扑克牌共计54张(包含大小王)，至少抽出几张就能保证一定有两张牌的花色相同?
A.5 B.6 C.7 D.8
【答案】C【解析】考虑最不利的情况，即先取出不满足题意的大小王两张，其余四种花色每一种都取 1 张牌，此时再抽一张牌，这一张一定是四种花色中的某一种，就构成了 2 张牌花色相同，即抽 2+4+1=7(张)。故正确答案为C。
【例题2】200人参加招聘，工、理、文科各130、40、30人，至少有多少人找到工作才能保证有40人专业相同?
A.41 B.69 C.110 D.109
【答案】D【解析】考虑最不利情况，即先将肯定无法满足要求的文科30人抽完，再从工、理科分别抽取39 人，此时再抽一个人，无论此人是工科还是理科，都能够和前面已有的39人凑成40人专业相同。此时至少有 30+39+39+1=109人找到工作就能保证有40人的专业相同，故正确答案为D。
【例题3】一把钥匙只能开一把锁，现有10把钥匙和10把锁，至少要实验多少次就能够保证全部的钥匙和锁相匹配?
A.9 B.10 C.35 D.45
【答案】D【解析】考虑最不利的情况，拿出第一把钥匙试了9把锁都不对，此时不用再试，这把钥匙必定是剩下的最后一把锁的，即第一把锁最不利的情况是实验9次;同理，第二把钥匙最不利的情况是前8次都不对，即试8次一定可以保证匹配成功;……;因此，要想所有的钥匙和锁相匹配，最不利的情况为总共实验9+8+7+6+5+4+3+2+1=45次。故正确答案为D。
