行测数量关系：多次相遇、流水行船问题及不定方程如何解
行测数量关系：多次相遇问题
行程问题是行测问题中必考题型，同时也是难点题型，因为它具有多种变形考察，比如相遇问题，甚至多次相遇问题，此时仅仅依靠“路程=速度×时间”这一简单公式，是不够的，我们需要从原理上理解多次相遇，才能更快更准确地解答此类问题。
首先我们来回忆一下什么叫“相遇问题”：
甲乙两人分别从A、B两地同时出发，相向而行，最终在两地之间相遇
这就是相遇问题最基础的描述，在这个过程中，我们有一个相遇问题的基本公式
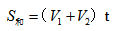
其中S和代表甲乙两人的路程和，一般既AB之间的距离，V1和V2代表甲乙两人的速度，t代表两人相遇的时间。
那么多次相遇的描述则会有如下改变：
甲乙两人分别从A、B两地同时出发，相向而行，在两地之间相遇之后继续前行，到达对方起点后立即掉头，如此反复。
我们发现，因为两人在AB之间来回行走，自然会在之间反复遇见，这个过程就叫多次相遇。我们用画图的方法来帮助大家理解：
从出发到第一次相遇，如图所示，我们可以得到一些量，比如两人的路程和S，两人的相遇时间t，以及甲乙各自行走的路程S甲和S乙
然后两人从①点继续行走，到达终点后立即返回，在②点第二次相遇：此时我们发现，甲乙所走的路程和为两倍的AB，也就是2S，因为两人速度都不变，则此段时间为2t，同理甲乙各自走的路程为2S甲和2S乙
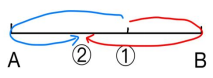
由此类推，两人从②点继续行走到③点相遇的话，甲乙所走的路程和为依旧为两倍的AB，也就是2S，因为两人速度依旧都不变，则此段时间仍为2t，同理甲乙各自走的路程仍为2S甲和2S乙
继续推导可得，从第三次相遇点到第四次相遇点、从第四次相遇点到第五次相遇点……，各种量皆满足此规律，列表表示：
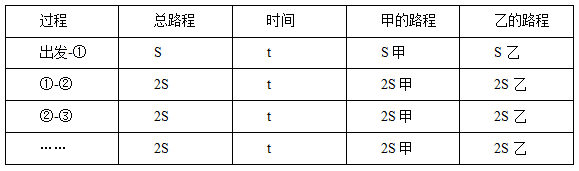
如果把每次相遇都从开始出发算起，那么以上各个数据将会变为：
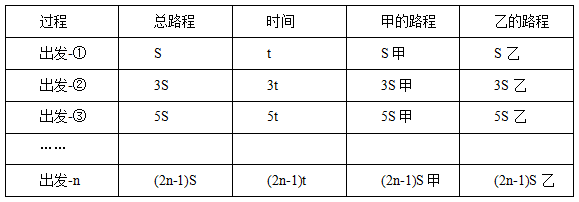
有了这些数据之间的关系，我们解决多次相遇问题就方便多了:
【例1】甲从A地、乙从B地同时以均匀的速度相向而行，第一次相遇离A地6千米，继续前进，到达对方起点后立即返回，在离B地3千米处第二次相遇，则A、B两地相距多少千米?（ ）
A.10 B.12 C.15 D.18
【答案】C【解析】由题意知第一次相遇甲走了6千米，因为相遇两次，则甲共走过了6×3=18千米，此时甲应走完一个全程多3千米，所以两地相距18-3=15千米。故正确答案为C。
行测数量关系：流水行船问题
程问题是行测考试数量关系中常考的一类题型，而行程问题其实也有很多类型，比如说相遇追及问题、牛吃草问题、流水行船问题等，其实这些题型的解题思路和方法也非常固定。接下来，就带着大家学习一下流水行船问题。
流水行船问题，是指船在河里航行时，除了船本身的速度外，还受到水流给船的推力或者阻力，因此，流水行船问题中基本公式为：
接下来通过例题来看一下具体怎么解流水行船问题：
【例1】一只船沿河顺流而行的航速为30千米/小时，已知按同样的船速在该河上顺水航行3小时和逆水航行5小时的航程相等，则此船在该河上顺水漂流半小时的航程为( )。
A.1千米 B.2千米 C.3千米 D.6千米
【答案】C【解析】根据航程相等，我们可以列出式子：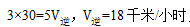
;顺水漂流也就是只有水流速度，
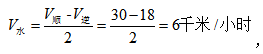因此顺水漂流半小时所走的路程=6×0.5=3千米。
除了一些简单的流水行船问题外，还有相对复杂一些的流水行船变形问题，我们来一起看一下吧!
【例2】商场的自动扶梯以匀速由下往上行驶，两个孩子在行驶的扶梯上上下走动，女孩由下往上走，男孩由上往下走，结果女孩走了40级到达楼上，男孩走了80级到达楼下。如果男孩单位时间内走的扶梯级数是女孩的2倍。则当该扶梯静止时，可看到的扶梯梯级有多少级?）（ ）
A.60 B.50 C. 40 D.30
【答案】A【解析】在一个自动扶梯上两个孩子上下走动，除了本身的速度外，自动扶梯也会给他们一个速度，因此我们可以用流水行船去解题。设女孩的速度为 v1，则男孩的速度为 2v1，自动扶梯的速度为 v2。因为女孩是和扶梯同向的，因此女孩从楼下到达楼上的总扶梯数应该是女孩自己走的加上扶梯走的，而女孩走了40级到达楼上可得：S=40+v2t1;①v1×t1=40;②而男生和扶梯是反向的，因此男孩从楼上到达楼下的总扶梯数应该是自己走的减去扶梯走的，而男孩走了80级到达楼上可得：S=80-v2t2;③2v1×t2=80;④最后让我们求扶梯静止时有多少级，也就是实际的总扶梯数S为多少，很明显我们可以根据前面建立的4个式子进行求解，观察等式能发现我们可以将②和④分别带入到①和③得到：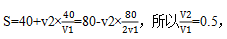
因此S=40+0.5×40=60级。故正确答案为A。
相信大家通过前面的讲解，对于流水行船问题已经有了初步的了解，在之后的学习过程中，大家遇到同类型的问题时，可以参照我们前面讲解的方法进行解题，应该就能得心应手啦!
2022国考行测数量关系不定方程如何解
每年国考，对数量关系的考查中计算问题往往少不了，而不定方程又是计算问题中常考的一个知识点，今天带领大家一起来学习一下不定方程。
何为不定方程
未知数的个数多于独立方程的个数，这样的方程(组)叫不定方程。例如：
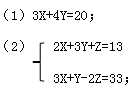
1、代入法：把选项代入题干当中，选出正确答案。
【例1】3X+8Y=36，已知X，Y为正整数，则Y=( )。
A.1 B.3 C.5 D.7
【答案】B【解析】代入A选项，Y=1，即3X+8×1=36，3X=28，解出X不是正整数，排除;代入B选项，Y=3，即3X-8×3=36，3X=12，X=4，符合题干要求;同理代入C，D求出X会发现不符合题干要求，此题正确答案为B。
2、整除法：某个未知数的系数与常数有公约数时，另一个未知数必为该公约数的倍数。
【例2】4X+7Y=40，已知X，Y为正整数，则Y=( )。
A.1 B.2 C.3 D.4
【答案】D【解析】根据题目可知：4,40有公约数4，而7不是4的倍数，所以Y是4的倍数，所以正确答案为D(简单理解：4的倍数+?=4的倍数，?必为4的倍数，而7不是4的倍数，所以Y是4的倍数)。故正确答案为D。
3、奇偶法：未知数系数有奇数有偶数，可根据奇偶性求解。
知识补充：偶数±偶数=偶数，偶数±奇数=奇数，奇数±奇数=偶数;
偶数×偶数=偶数，偶数×奇数=偶数，奇数×奇数=奇数。
【例3】4X+5Y=23，已知X，Y为正整数，则Y=( )。
A.2 B.3 C.4 D.6
【答案】B【解析】根据题目可知：23为奇数，4X为偶数，即5Y为奇数，5是奇数，则Y也为奇数，结合选项，此题正确答案为B。
4、尾数法：当未知数系数是5或是5的倍数，可以根据尾数确定答案。
【例4】10X+3Y=41，已知X，Y为正整数，则Y=( )。
A.5 B.6 C.7 D.8
【答案】C【解析】根据题目可知：41的尾数为1,10X的尾数为0，则3Y的尾数应该为1，结合选项当Y=7时，3Y的尾数为1，所以正确答案为C。
以上四种方法就是我们解决不定方程在正整数范围内的常用方法，希望大家可以学会。
