
行测数量关系的几个技巧,赶紧收藏起来吧!
行测指导:概率问题之多次独立重复试验
近年来,公务员考试不断推陈出新,对比之前的常规题目而言,所测查考点在原有的基础上更加综合。今天给大家带来的是概率问题当中的多次独立重复试验,其解题核心在于熟悉题型特征,公式的理解及记忆。
什么是多次独立重复试验?
在同样的条件下重复地、各次之间相互独立地进行的一种试验。
题型特征
这种试验中,每一次试验只有两种结果,即某事件A要么发生,要么不发生。并且每次发生的概率都是相同的。
重点公式
某一实验独立重复n次,其中每次试验中某一事件A发生的概率是P,那么事件A出现k次的概率为P=
示例
在某次射箭活动中,某人每次命中10环的概率为0.8,那么在4次射箭中,共有2次命中10环的概率是多少?
【解析】:每次命中10环的概率互补影响,所求概率为。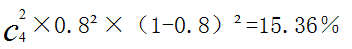 【例1】甲和乙进行打靶比赛,各打两发子弹,中靶数量多的人就获胜。甲每发子弹中靶的概率是60%,而乙每发子弹中靶的概率是30%,则比赛中乙战胜甲的可能性有多大?( )
【例1】甲和乙进行打靶比赛,各打两发子弹,中靶数量多的人就获胜。甲每发子弹中靶的概率是60%,而乙每发子弹中靶的概率是30%,则比赛中乙战胜甲的可能性有多大?( )
A.小于5% B.5%~10% C.10%~15% D.大于15%
【答案】C。【解析】:乙战胜甲有3种可能性:(1)乙中一发,甲中零发。(2)乙中两发,甲中一发。(3)乙中两发,甲中零发。则(1)发生的概率为 (2)发生的概率为
(2)发生的概率为 (3)发生的概率为30%²×(1-60%)²=0.0144。综上所述,乙战胜甲的概率为0.0672+0.0432+0.0144=12.48%。故正确答案为C。
(3)发生的概率为30%²×(1-60%)²=0.0144。综上所述,乙战胜甲的概率为0.0672+0.0432+0.0144=12.48%。故正确答案为C。
随着公考的不断发展与变迁,数量关系的问题向着更综合的考查方向延伸,对于组成杂乱的数学问题我们要在平时的练习中多加积累,对于基本的结论要做到运用自如,会给解题带来更多的便捷。相信通过以上的公式总结,以及例题解析,考生们对于这种题型已经掌握了。
行测备考技巧:分数比较大小之差分法
分数比较大小的方法有很多种,有些比较可以直接心算首位看出大小关系,但是有些分数比较接近,直接笔算比较麻烦花费时间较长,因此今天带大家来看一看比较大小中的差分法。
差分法的适用环境与步骤
适用环境: 型比较大小。
型比较大小。
名词解释:①大分式指分子分母均较大的分式,小分式同理;
②差分式为两个分式的分子之差除分母之差。
步骤:①做出两个分式的差分式;
②将大分式放在差分式和小分式之间;
③将差分式与两个原分式中较易观察出来的分式比较,得出大小关系,该大小关系具有传递性,三个分式之间的符号均取决于得出的大小关系。
典型例题
【例1】比较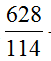 与
与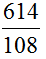 的大小。
的大小。
解析:构造差分数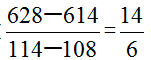 ;将大分式放在差分式与小分式的中间,形成如右所示
;将大分式放在差分式与小分式的中间,形成如右所示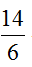 、
、 ,明显能看出差分式最小,小于右边,因此整体填小于号,即
,明显能看出差分式最小,小于右边,因此整体填小于号,即
原理解析
差分法的原理其实很简单,和浓度混合问题有异曲同工之妙。我们将各个分式看成溶液的浓度,差分式由两个分式的分子之差除分母之差,因此我们可以将大分式看成一个由小分式和差分式这两种浓度的溶液混合而成的溶液。那么根据浓度混合的原理,我们可知混合后的溶液浓度一定界于两种溶液的浓度之间,即大分式的大小一定在小分式和差分式之间。因此,只要判定出差分式与两个分式中任意一个的大小关系即可判断出原分式之间的大小关系。
差分法比较大小胜在将除法转化为减法,相对而言较简单易判断。但判断 型大小关系,首先还是看能否用观察法看出大小关系,之后再考虑用差分法。
型大小关系,首先还是看能否用观察法看出大小关系,之后再考虑用差分法。
行测数量关系:学会“植树”的小窍门
植树问题是行测考试常见的题目之一,这类题目本身比较容易,需要注意题目本身的特点即可,与剪绳子问题类似,本质上来讲就是考虑端点与段数之间的关系。今天就来研究直线上的植树问题以及环形植树问题。
1.直线上植树问题
我们可以把树看做直线上的端点,如果有两棵树的话就形成一段间隔;三棵树的话,形成两个间隔,以此类推。这样我们会看出来,在直线上植树的时候,树的数量始终要比间隔的数目多一个。因此当直线一侧植树时,我们得到,棵数=总长÷间隔+1;总长=(棵数-1)×间隔。
【例1】在一条公路两侧种植10棵树,任意两棵树之间的距离为30m,那么第一棵树到最后一棵树的距离为多少?( )
【解析】两侧总共有10棵树,算距离时我们算单侧即可,单侧每侧植5棵,那么就只有4个间隔,一个间隔距离为30m,总长度为120m。
2.环形上的植树问题
环形是一个闭合的回路,有几个端点之间就形成几个间隔。植3棵树就有三个间隔,原理就在于,在环形上相当于把直线闭合,这样第一棵和最后一棵树之间是重合的关系,是没有间隔的,所以环形上,树的数量和间隔的数量是一样的。因此在环形一侧植树时,我们就可以得到:棵数=总长÷间隔;总长= 棵数×间隔。
【例2】在一个环形跑道种植50棵树,任意两棵树之间的距离为30m,那么环形跑道的周长为多少?( )
【解析】环形跑道有50棵树,就有50个间隔,一个距离为30m,则环形跑道的周长为1500m。
【例3】小刘匀速地在楼道内爬楼梯锻炼身体,她从第一层楼房走到第六层共用6分钟,已知每两层楼房的间距都相等。那么小刘再用18分钟,能从第六层爬到第几层楼房?( )
A.15 B.16 C.20 D.21
【答案】D。【解析】实际上这道题是植树问题的变形,每层楼相当于树,而层与层之间的楼梯相当于树之间的间隔,从第一次走到第六层一共经历5个间隔,小刘走在楼梯(间隔)上才花费时间,所以6min可以走5个间隔,再过18min可以走15个间隔,从六楼往上,每走一个间隔就登上一层,因此,再走15层,走到21层。故正确答案为D。
通过例题相信同学们能够明白,我们在处理植树问题时,至需要判断是直线还是曲线后,把握好端点与间隔之间的关系即可。
行测数量关系:计算问题一大类,等差数列要做对
公职类考试数量关系题目中,计算问题为较大一类题型,涵盖知识点较多,学起来相对复杂,然而这类题目中有一类虽然涉及高中知识点,但只要我们理解好还是可以拿分的,那就是等差数列类型题目,今天通过两道题目来学习一下等差数列的解题过程:
【例1】某剧院有33排座位,后一排比前一排多3个座位,最后一排有135个座位。这个剧院一共有( )个座位。
A.2784 B.2871 C.2820 D.2697
【答案】B。【解析】方法一:由题干可知,共有33排座位,后一排比前一排多3个,即从第二排开始,后一排座位数减前一排座位数为定值3,说明33排座位数构成了公差d=3的等差数列,已知 根据等差数列通项公式
根据等差数列通项公式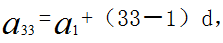 得,
得,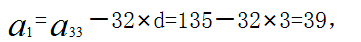 则所求33排座位数之和
则所求33排座位数之和 故正确答案为B。
故正确答案为B。

【例2】某工厂11月份工作忙,星期日不休息,而且从第一天开始,每天都从总厂陆续派相同的工人到分厂工作,直到月底,总厂还剩工人240人。如果月底统计总工厂工人的工作量是8070个工作日(一人工作一天为1个工作日),且无人缺勤,那么,这月由总厂派到分厂工作的工人共有多少人?( )
A.2 B.60 C.240 D.298

小结
两道等差数列题目并不难,其实更多是想告诉小伙伴们,做到此类问题首先我们需要判定出题干描述为等差数列,其次,是熟悉等差数列的通项公式和求和公式,最后根据所求问题一步步求解即可,小伙伴们一定要巩固学过的基础理论公式,等差数列问题即可迎刃而解。
行测数量关系答题技巧:逆水行舟,不进则退
古语有云学如逆水行舟,不进则退;心似平原走马,易放难追。在成长的道路上,我们并不陌生学习二字,如果说对于一件事坚持了十年便是专家了,那我们也能在一定角度上称为学习上的专家了,但是现在的我们却不断的被各种考试打击,在不断的打击下,我们依然坚持,这就是我们当代青年的优点之一,我们会吐槽会抱怨,但是我们从不放弃为了梦想而努力。此句话并不仅仅是在激励大家,更是希望大家注意行测考试里的一个题型,即流水行船问题。
在大江大河中航行时,船除了本身速度以外,还要受到流水的推动,在这种情况下核算船只的航行速度、时间和所行的路程,即为流水行船问题。
因为船只需要考虑到流水的速度,所有在计算该问题时,分为顺水速度和逆水速度,其中:顺水速度=船速+水速;逆水速度=船速-水速。
【例1】甲、乙两个港口之间的距离为120千米。甲港口滞留了180人,要将这些滞留乘客顺流送到乙港口。现派甲港口的一艘可乘坐100位乘客的客船来完成送达任务。已知该客船在静水中的速度为90千米/小时,顺流行驶的速度是100千米/小时。在忽略上下船时间的情况下,该客船完成任务需要多少小时?( )
A.2.7 B.3.2 C.3.5 D.3.9
【答案】D。【解析】甲港口一共180人,每次只能送100人,故需要送两次,送两次的过程也就是从甲前往乙顺流一次,乙返回甲逆流一次,甲再返回乙一次;客船在静水中速度为90千米/小时即为船速,顺流而下是速度为100千米/小时,走一趟顺水是时间为:120/100=1.2小时;且水速=顺水速度-船速=100-90=10千米/小时,所以客船逆水速度=船速-水速=90-10=80千米/小时走一趟逆水的时间:120/80=1.5小时;则共需要1.2×2+1.5=3.9小时。故正确答案为D。
当然流水行船问题的题目背景不一定都是在大江大河里航行,更多的是在一个运动的物体还存在另一个力,导致运动速度被改变。例如逆风奔跑的你,是吗?
【例2】一位少年短跑选手,顺风跑90米用了10秒,在同样的风速下,逆风跑70米,也用了10秒,则在无风的时候,他跑100米要用多少秒?( )
【答案】该少年在无风时的速度为: 则无风中他跑100米需要100/8=12.5秒。
则无风中他跑100米需要100/8=12.5秒。
在该题中,我们发现解答不同的题型,也是可以利用同样的方法,这就是灵活多变的数学题,万物变化那么多,但是只要抓住基础题型,我们还是能够很快完成进阶题型。要善于总结,善于发现,这样才能够让我们在有限的时间里学到更多的题目。








