政华教育

在公务员考试中每年都必然有数量关系，从近几年的命题规律来看数量关系普遍考查10到15题，数量关系的题目被广大考生认为是耗时、不好做或者没时间做的题目，还有诸多考生这样安慰自己“大家都放弃，我也放弃”。其实你的公考路或许就差两道数量关系的距离。所以今天给大家介绍如何克服心理恐惧，抓住数量关系的送分题。

一、放平心态，能学多少是多少

平时复习的时候数量关系中遇到简单计算，特值，工程多尝试用方程解题，能读懂，能列式就把题目做出来，做不出来也不必有思想负担，但是绝对不是在备考时就抱有直接放弃数量的心态。

【例】某饮料厂生产的A、B两种饮料均需加入某添加剂，A饮料每瓶需加该添加剂4克，B饮料每瓶需加3克。已知370克该添加剂恰好生产了这两种饮料共计100瓶，则A、B两种饮料各生产了多少瓶？

A.30、70 B.40、60 C.50、50 D.70、30

【解析】D。设生产A饮料x瓶，B饮料y瓶，由题意可知 x+y=100，4x+3y=370，解得 x=70，y=30。故本题选D。

二、注重生活经验积累，跳脱常规思维算笔账

很多问题其实用生活常识看一看，用简单的思维去分析也可以看出选项：

A.30、70 B.40、60 C.50、50 D.70、30

【解析】D。假设100瓶全是A则需要400g添加剂，假设100瓶全是B则需要300g添加剂，实际用的添加剂是370g很接近400g，所以A种饮料必然数量更多，故本题选D。

三、善于运用特殊技巧“整除”、“特值”、“比例”等

省考中很多题目可以运用一些小技巧达到快速解题的目的，比如说整除，比例，特值的方法解题一定可以快速锁定选项。对于数量关系平时应加强一些简单技巧的总结，争取最大可能的得分。

【例】每年三月某单位都要组织员工去A、B两地参加植树活动。已知去A地每人往返车费20元，人均植树5棵，去B地每人往返车费30元，人均植树3棵，设到A地员工有x人，A、B两地共植树y棵，y与x之间满足 y=8x-15，若往返车费总和不超3000元，那么，最多可植树多少棵？

A.498棵 B.400棵 C.489棵 D.500棵

【解析】C。因为要求的是植树的棵树，也就是求y的值，x和y都是整数，y=8x-15，8x必是偶数，则偶数减去奇数15，y必是奇数，只有C。

考试中数量可以放在第一或最后一个版块来做，切记不可贪，不可太过重视，也不可直接放弃，以最平常的心态抽出题干最短的五道题目大致分析做题即可，能做出来其中三四道题目也就很正常了，降低标准迎难而上，相信一定有所突破。

行测备考技巧：定位法求解概率问题，你会吗？

在同学们行测备考时，遇到概率问题，大家肯定还是比较陌生的，感觉自己会，但是好像自己又不会，想做又不知道做得对不对，所以错误率相对较高一些，那么概率问题如何能够做对呢？今天跟着一起来看一看概率问题，有的时候我们也可以做出来的，只要掌握其中的技巧，同样可以把题目求解出来。我们来看一道题目，来体会一下概率问题是如何求解的。

【例】一张纸上画了5排共30个格子，每排格子数相同，小王将1个红色和1个绿色棋子随机放入任意一个格子(2个棋子不在同一个格子)，则2个棋子在同一排的概率：

A.不高于15% B.高于15%但低于20%

C.正好为20% D.高于20%

【解析】B。这道题目其实就是让我们把棋子放到格子里面，然后求解2个棋子在同一排的概率，该事件样本为有限个，同时也是等可能事件，所以满足古典概率问题，那么总的等可能事件样本数是多少呢？2个棋子不在同一个格子，那么其实就是将2个不同棋子放到30个格子当中，那么就有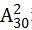种方法。目标所求等可能事件样本数又为多少呢？由于有5排共30个格子，每排格子数相同，所以每排就有6个格子，想在一排就需要在6个格子中选择两个格子放两个棋子，就有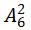种不同方法，但是一共有5排，究竟放在哪一排当中呢，有5排可以选择，所以还要再乘上5，因此本道题的概率就为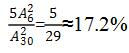：，这道题答案选择B。这个方法是常规求解概率问题的方法，那么我们现在想想，要想两个棋子在一排，我可以一个棋子一个棋子的放，那重点在第一个棋子还是第二个棋子呢？实际我们就发现，第一个棋子实际上可以随便放，只要保证第二个棋子放的时候和第一个棋子在同一排即可，那么第一个棋子随便放，第二个棋子在放的时候就只有29种选择了，那么这剩下的29种选择中，又有几个格子使两个棋子可以在同一排呢，一排6个格子，第一个棋子已经占了一个了，那么剩余5个格子可以使两个棋子在同一排，因此本道题答案可以直接写成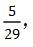直接选择B选项。

其实我们可以看到，这道题目我们实际上就是，刚开始用的是常规做法，计算和列式上却要麻烦一些，但是定位法在解决该问题的时候，就省了很多步骤，因此解题要有一个清晰的思路，我们只需搞清楚事情需要做哪些即可，把事情捋顺捋清楚，就可以做出来这个题目。因此这类题目希望各位备考的考生能够用对方法，快速地把问题求解清楚，找准方向即可求解出相应的结果。最后希望大家能够跟上的脚步，每天都有所收获，早日成功。

整除思想快速解国考行测数量关系题

考生们往往觉得数量关系的题目非常的难，所以在平时的备考过程当中呢，对于数量关系的备考，基本上处于一个放弃的状态，但是其实要想真正在国考当中取得一个不错的分数，数量关系肯定是不能放弃的，其实有些数量关系的题目是可以根据我们的方法快速选出答案的。给大家介绍的就是整除法。

什么时候可以用整除呢？首先我们来给大家讲解一下整除的应用环境：

1.文字表述整除“倍”，“每”，“平均”，“整除”)

2.数据体现整除(小数，分数，百分数，比例)

【例1】两个派出所某月内共受理案件 160 起，其中甲派出所受理的案件中有 17%刑事案件，乙派出所受理的案件中有 20%是刑事案件，问乙派出所在这个月中共受理多少起非刑事案件？

A.48 B.60 C.72 D.96

【解析】A。乙非刑事：乙案件=4：5，得到答案应该能被4整除，无法排除答案，又因为甲刑事：甲案件=17：100.根据总案件160件可以得出甲应该是100件，乙应该是60件，因此答案应该是60*80%=48，答案为A。

【例2】某单位组织员工去旅游，要求每辆汽车坐的人数相同。如果每辆车坐 20 人，还剩下 2 名员工；如果减少一辆汽车，员工正好可以平均分到每辆汽车。问该单位共有多少名员工？

A.244 B.242 C.220 D.224

【解析】B。总人数-2能被20整除，答案为B。

【例3】哥哥现在的年龄是弟弟当年年龄的3倍，哥哥当年的年龄与弟弟现在的年龄相同，哥哥与弟弟现在的年龄和是 30 岁。问哥哥现在多少岁？

A.15 B.16 C.18 D.19

【解析】C。哥哥的年龄能被3整除，答案排除B，D，又因为哥哥和弟弟年龄和为30岁，如果哥哥的年龄为15，就和弟弟年龄一样，不符合题意，因此答案选C.

【例4】已知张三和李四都养有一些猪，都是黑毛猪和非黑毛猪，一共是260头，但现在李四因为有事将自己的猪和李四的猪放一起，已知张三的猪有13%是黑毛猪，李四的猪有12.5%是黑毛猪，则李四的非黑毛猪有多少只？

A.120 B.140 C.160 D.200

【解析】B。由其中的百分数知道其可以化为分数，而李四的猪有八分之一为黑毛猪，则非黑毛猪为八分之七，则应为7的倍数，从而选择B。

综上所述，数量关系其实对于大家来说，学会把简单的题目挑选出来做对是备考的关键。

行测数学运算统筹问题之方案配组

在数学运算的题目中，有一种题型十分贴近我们的生活，就是统筹问题。统筹问题研究如何运用人力物力使它们发挥最大效率的一种问题。今天我们一起来学习统筹问题的其中一个考点：方案配组问题。这类题目中会涉及不同的购买方案或运输方案，我们需要根据价格因素或运输成本因素，从而找到最优方案。接下来带大家一起完成两道例题，总结出此类问题的解题方法。

【例1】某公司要买100本便签纸和100支胶棒，附近有两家超市。A超市的便签纸0.8元一本，胶棒2元一支且买2送1。B超市的便签纸1元一本且买3送1，胶棒1.5元一支。如果公司采购员要在这两家超市买这些物品，他至少要花多少元钱。

A.183.5 B.208.5 C.225 D.230

【解析】B。对于便签纸而言，A超市单价为0.8元一本，B超市1元一本，但是买3送1，每4本为一组，单价为3÷4=0.75元。B超市更便宜，花费100÷4×3=75元。

对于胶棒而言，A超市单价为2元一支，但是买2送1，每3支为一组，单价为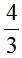元，B超市1.5元一支，A超市更便宜，尽可能在A超市购买。100支可以分为33组再多一支，33组在A超市购买，多的一支在B超市购买，共花费2×2×33+1.5=133.5元。

则两样商品一共需要花费75+133.5=208.5元，故本题选B。

【例2】某高校为了接新生报到，决定派校车前往接站。现已知该校有A、B两种类型校车。A型校车往返一次耗油25升，一次接送学生46人，B型校车往返一次耗油18升，一次接送学生28人，现有525位学生需要接站。为使耗油最少，A车需出的车次是( )。

A.9 B.12 C.11 D.10

【解析】C。A 型车每人油耗A型车单位油耗更少，所以尽量用 A 车，525÷46=11……19，即用 A 车接 11 次，剩下的人可以 B 车一次正好接完，故本题选C。

以上两道题，一道是如何购买最便宜，一道是如何派车耗油最少，但我们解题重点都是先确定不同情况下的单价或者单位油耗，进行比较，从而优先选择成本低的方案。因此解决这类题型，我们只需要比较不同方案的单位成本，再进行计算即可，这类题型难度不大，希望大家可以灵活掌握。

行测数量关系：求解最不利情况数三大步骤

在备考行测数量关系时，有很多题目计算量一般不大，但是需要思考的比较清楚，例如极值问题的最不利原则，大家往往都知道这种题型的解法，是用最不利的情况数+1，但是大家往往想不清最不利的情况到底是怎样，所以接下来就给大家分享，最不利情况数如何快速找到，各位考生着重掌握求解最不利情况数三大步骤。

前提是先将题目转换为标准问法，即“至少……才能保证……相同”，然后三步走：

1.找品种数，即“保证”后面，“相同”前面的名词；

2.保证n个，往每个品种数里面放n-1个数；

3.汇总即为最不利情况数。注：特殊情况(怎么样都不能够满足要求的情况)

【例1】现有梅花、红桃、黑桃、方块扑克牌各10张，混放在一个暗箱里，一次至少摸出多少张，才能保证有6张卡片花色相同？

A.15 B.21 C.25 D.30

【解析】(1)找品种数，“保证”后，“相同”前的名词是“花色”，所以品种数是4种(梅花、红桃、黑桃、方块)；(2)保证6张花色相同，每个品种下面放(6-1=5)5张；(3)汇总，所以最不利的情况数为4×5=20人。

这种情况下，再任选1张，就能保证有6张牌花色相同，所以结果数为20+1=21，故选择选项B。

【例2】在一个不透明的布袋里有若干条四种不同颜色的围巾，其中白色3条，红色5条，蓝色8条，彩色6条。如果每次取出一条，至少要取( )次才能保证有5条围巾颜色相同？

A.15 B.16 C.17 D.18

【解析】B。(1)找品种数，“保证”后，“一样”前的名词是“围巾颜色”，即品种数为4(白、红、蓝、彩)；(2)保证5条颜色相同，每个品种数下放5-1=4条；(3)汇总，注意特殊情况(白色只有3条，不可能有4条)，所以最不利的情况数：4×4+3=15条。

这种情况下，再取一条围巾，就能保证有5条围巾颜色相同，所以结果数为15+1=16，故选择选项B。

通过两个例题，相信各位考生对最不利情况数解题步骤有了全新思维，多多练习题目。