
提升行测数量关系方法学习
行测数量关系:方程之其“举足轻重”
数学运算是公职考试中不可或缺的一部分,同时数学运算也成了大多数考生备考过程中的一块硬石头。本文带各位考生一起碰碰这个硬石头,如此硬石头用软拳头“方程”解决最为妙不可言,所以方程法在数量关系的题目解决过程中是有着“举足轻重”的地位的。
例题:六一儿童节期间,100名幼儿园学生参加5项活动,参加人数最多的活动人数不超过参加人数最少的活动人数的二倍,则参加人数最少的活动最少有多少人参加?
【解析】在这道题目中我们已知参加5项活动的总人数100,同时,题目问的是参加人数最少的活动最少有多少人参加。属于和一定求某个数的最小值。那要保证某项活动参加人数最少,其他活动的参加人数要尽可能多。然而在这道题目中并没有规定每项活动的参加人数要互不相等,所以要让参加活动人数最少的项目参加人数最少我们可已让其他项目的参加人数相等且都等于最多的那一项的人数,因为参加人数最多的活动人数不超过参加人数最少的活动人数的二倍,所以最多的项目参加人数最多应该等于参加人数最少的活动人数的二倍。假设参加人数最少的活动人数为X,那其他项目的参加人数均为2X,则有X+2X+2X+2X+2X=100,9X=100,X≈11.1。有因为X代表的是参加人数最少的活动的参加人数,所以应该为整数,那么X应该为不小于11.1的整数,那X最小应该取到12。
例题:某玩具厂车间生产一批玩具,原计划每天生产100个,但实际生产过程中每天的生产量为120个。结果提前4天完工,还多生产了80个,则该玩具厂原计划生产玩具( )个?
【解析】在这道题目中,可根据原计划工作量和实际完成工作量之间的关系,建立等量关系,设原计划生产t天,则原计划生产100t个零件,根据“实际多生产了80个”,可得100t+80=120(t-4),解得t=28,即原计划生产28天,故原计划生产零件100t=100×28=2800个。
例题:软件园投入一笔资金用于奖励院内优秀企业。如果评出的优秀企业占总企业数的10%,每家奖励100万元,资金将结余150万元;如果评出的优秀企业占25%,每家奖励50万元,则还需要额外投入200万元。问软件园共有多少家企业?( )
【解析】在这道题目中,可根据计划投入的奖金预算一定,建立等量关系,假设软件园共有X家企业,软件园投入资金前后保持不变,根据题意有10%X×100+150=25%X×50-200,解得X=140。
通过以上三个题目可以看出,在数量关系中多种题型均可借助基本方程来解决。
行测数量关系之牛吃草问题
在行测数量关系的备考中,部分考生碰到小题型时总是手足无措,在解决了一个题目之后却不能举一反三,达不到复习的效果。本文将向各位考生介绍小题型之一:牛吃草问题,牛吃草问题这种题型的特点是非常明显的,真正弄懂了以后,这些看起来有难度的题都会迎刃而解了!
先来看一道牛吃草问题的典型例题:
例题:牧场上有一片青草,每天都生长得一样快。这片青草供给10头牛吃,可以吃22天,或者供给16头牛吃,可以吃10天,期间一直有草生长。如果供给25头牛吃,可以吃多少天?( )
A.5 B.5.5 C.6 D.6.5
【答案】B。【解析】假设草继续生长,牛在吃,相当于是在牛在追草,属于追及问题,结合追及问题基本计量关系,那么追及距离即原有草量=牛吃的草量-草新生长的量,则原有草量=(牛每天吃掉的草量-每天生长的草量)×天数;设每头牛每天吃一份草,草每天长x份,可以供25头牛吃t天,则有(10-x)×22=(16-x)×10=(25-x)t,解此方程即得x=5,t=5.5。
根据例题发现,此类问题均属追及问题,结合原有草量=(牛每天吃掉的草量-每天生长的草量)×天数,所以可以总结出牛吃草问题的解题公式:(N1-x)×T1=(N2-x)×T2=(N3-x)×T3;那么如何识别是不是牛吃草问题呢,其实不见得必须有牛有草,只要符合以下三个特征即可:
(1)存在类排比句;
(2)原有量为定值;
(3)有两个因素的制约。
我们再看两道练习题检验一下学习效果。
例1:某水库共有10个泄洪闸,当10个泄洪闸全部打开时,8小时可将水位由警戒水位降至安全水位;只打开6个泄洪闸时,这个过程为24个小时,如水库每小时的入库量稳定,问如果打开8个泄洪闸时,需要多少小时可将水位降至安全水位?( )
A.10 B.12 C.14 D.16
【答案】B。【解析】设泄洪闸每小时泄洪量为1,水库每小时的入库量为x,所求为t小时。根据牛吃草问题的公式有:(10-x)×8=(6-x)×24=(8-x)×t,解得x=4,t=12。
例2:某河道由于淤泥堆积影响到船只航行安全,现由工程队使用挖沙机进行清淤工作,清淤时上游河水又会带来新的泥沙(假定每天的泥沙量恒定)。若使用1台挖沙机300天可完成清淤工作,使用2台挖沙机100天可完成清淤工作。为了尽快让河道恢复使用,上级部门要求工程队25天内完成河道的全部清淤工作,那么工程队至少要有多少台挖沙机同时作?( )
A.4 B.5 C.6 D.7
【答案】D。【解析】设每台挖沙机每天挖泥量为1,每天新增泥沙量为x,如果25天完成任务需要n台挖沙机,则根据“清淤工作开始时堆积的泥沙量相等”可列方程(1-x)×300=(2-x)×100=(n-x)×25,解得x=0.5,n=6.5,因此至少需要7台。故本题选D。
通过以上的学习,相信大家对牛吃草问题已经有所了解,以后遇到符合题型特征的题目,直接代入公式进行求解即可。
突破行测瓶颈 拿下数量关系
很多考生在行测备考过程中对于数量关系无从下手,也往往是因为数量关系的影响,迟迟无法突破瓶颈。那么究竟能否通过科学高效的备考,决胜数量关系,实现行测成绩的弯道超车呢?今天就给大家介绍下数量关系科学高效备考的四大步骤。
一、夯实基础:解题方法学习
工欲善其事必先利其器。行测考试时间紧,题量大,数量关系题目技巧性强,所以高效备考的第一步就是学习常用的解题方法,尤其是具有普适性、能够解决多种题型的方法。

二、重点突破:常考题型学习
知己知彼方能百战不殆。备考的第二步就是逐个突破常考题型,紧紧抓住“考什么,学什么”的基本原则。
数量关系重点考察的题型主要有计算问题(整除、和差倍比、等差数列、周期循环、简单计算等)、行程问题(环形相遇、牛吃草、普通行程、流水行船)、工程问题(多者合作)、几何问题(基本公式、解直角三角形、图形相似)、排列组合(常用方法和隔板模型)、概率问题(古典概率、几何概率、多次独立重复试验)、利润问题、容斥问题、极值问题。其中计算问题、排列组合、概率问题、几何问题更是重中之重。
在行测数量关系备考过程中,既要了解各种常考题型涉及的知识点,又要熟知常用的解题方法。
三、提升速度:题海强化训练
数量关系做题效率尤为重要,第三步就是通过刷题,提升大家的题感和知识掌握的熟练程度,基本在1-2分钟左右完成一道题目。
具体操作是分成两个阶段,第一阶段分题型进行训练,目的是进一步巩固各种题型的知识点,真正吃透,熟能生巧;第二阶段和省考题量一致设置套题,限定时间,培养题感,提升做题效率。
每次的训练完成之后,做好易错点的整理,形成错题笔记,发现自身弱项,中间穿插理论回顾,重点强化学习,难点逐个突破。
四、判断取舍:如何选择题目
备考第四步是提高对题目类型和难度的判断能力,同时掌握选题技巧,在做题过程中由易到难,避免“死磕”难题,得不偿失,在有限的时间内最大限度的得到数量关系的分数。
选题建议如下:选择前2-3题,一般中等难度偏下;选择题干短、数据少的题目;选择熟悉且普遍难度不大的题型,如计算、利润、行程、工程等。最后,再做其他信息量多、难度较大的题目。
大家需要在平时的训练中,培养对题目的敏感性并强化选题技巧,真正的从战术上多得到分数。
相信通过以上四步,各位考生能够提高数量关系备考效率,打破桎梏,突破瓶颈,真正的在数量关系上实现成绩的弯道超车。
行测排列组合不求人,隔板模型直接套
在行测考试中,数量关系虽然题量不多,但分值却不少。考试时间紧,很多同学又主观认为数量关系偏难,往往不给数量机会,尤其在面对数量关系中的常考题型排列组合时,在备考时都会选择性的避开,但其实排列组合中有一种比较典型的隔板模型,相对于其他的排列组合的题目来说,难度不大,只要掌握他的本质,就能融会贯通啦。接下来就带大家一起来学习一下隔板模型的相关知识吧!
一、什么是隔板模型
隔板模型本质上是同素分堆的问题,即将n个相同的元素分给m个不同的对象,每个对象至少分到一个元素,且要分完,问有多少种不同分法的问题。
二、隔板模型的条件
1.所分的元素必须完全相同
2.所要分的元素必须分完
3.每个对象至少分到1个
三、隔板模型的相关应用
例1:将9个完全相同的小球分给3个小朋友,要求每个小朋友必须分到至少一个球,球要分完,总共有多少种分法?( )
A.19 B.24 C.28 D.30
【解析】这个题满足隔板模型的所有条件,那要怎么样去思考呢?我们可以考虑先将小球一字排开,如图所示

此时我们观察到9个小球除了端头两个位置以外,会形成8个空位,也就是箭头所标注的位置,如果我们取两块板插入这8个空中的其中任意两个空位,都可以将这9个小球分成三份,并且满足每一份至少有一个小球,再把这三份分给三个小朋友,就可以满足每人至少一个球且球分完,所以8个空插两块板就共 种情况。选择C选项。
种情况。选择C选项。
由上题总结可得,若将n个相同元素分成m份,每份至少一个元素,共有 种情况。
种情况。
例2:小明要将30个一模一样的玩具球放入3个不同颜色的桶里面,每个桶至少放9个玩具球,问一共有多少种不同的放法?( )
A.12 B.11 C.10 D.9
【解析】此题直观的来看不满足隔板模型当中每个对象至少分一个的条件,但是可以通过转换使之满足,即给每个桶先放8个玩具球,剩下30-3×8=6个小球,再放到3个桶里,就可以将此题转化为“将6个玩具球放到三个桶里,每个桶至少放一个球”,所以利用公式共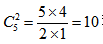 种分法,选C。
种分法,选C。
以上就是排列组合问题当中的隔板模型的解法及相关变形应用的巧解方式,所以了解隔板模型的本质后,这一类题型并不难,通过本文的讲解,你能识别出隔板模型的考察了么?希望各位考生在备考时打好坚实的基础,灵活使用各种方法解决这一类题目。








