
行测数量关系备考技巧
认识相遇追及 轻松应对行测行程问题
行程问题是行测数量关系的常考题型,相遇追及更是重中之重。同学们在面对这类问题往往找不到题干中的等量关系,以及理不清各自的行程轨迹,今天就带着大家一起来了解行程问题中的相遇和追及问题。
一、概念
相遇追及问题,是指两物体在同一直线或封闭图形上运动所涉及的追及、相遇等一类问题。
二、常用公式及运用
1.行程问题基本公式
路程=速度×时间(S=vt)
2.相遇追及模型及公式
(1)直线上的相遇与追及
直线上的相遇:路程和=速度和×相遇时间
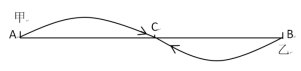
对于直线上的相遇问题,一般题目的题设条件为:甲乙两人分别从A、B两地同时出发相向而行,一段时间后在A、B之间的某一点C相遇……在这个过程中AB的距离等于甲所行驶的路程AC与乙所行驶的路程CB之和,而他们的路程分别等于各自的速度与时间的乘积,时间相同,则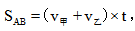 记为路程和=速度和×时间。
记为路程和=速度和×时间。
例1
甲乙两座城市相距530千米,货车与客车分别从两城出发,相向而行。货车每小时行50千米,客车每小时行70千米。客车因故比货车晚一小时出发,两车在途中某地相遇。问相遇时货车行驶多少千米?( )
A.100 B.150 C.200 D.250
【答案】D。【解析】设客车出发后,经过t小时两车相遇,作图如下,

根据相遇问题公式:路程和=速度和×时间,可知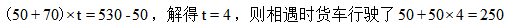 千米,故此题选择D选项。
千米,故此题选择D选项。
直线上的追及:速度差=速度差×追及时间
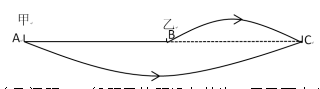
对于直线上的追及问题,一般题目的题设条件为:甲乙两人分别从A、B两地同时出发同向而行,一段时间后在B之后的某一点C甲追上了乙……在这个过程中AB的距离就是甲比乙多走的的路程,即甲所行驶的路程AC与乙所行驶的路程BC之差,而他们的路程分别等于各自的速度与时间的乘积,时间相同,则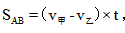 记为路程差=速度差×时间。
记为路程差=速度差×时间。
例2
甲以每小时6千米的速度步行从A地前往B地,在甲出发90分钟时,乙发现甲落下了重要物品,立即骑自行车以每小时12千米的速度追甲,终于在上午11点追上了甲。问甲出发时间是上午几点?( )
A.7 B.8 C.9 D.10
【答案】B。【解析】设乙从出发到追上甲经过的时间为t小时,结合题意作图如下,
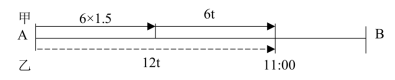 根据追及问题公式:路程差=速度差×时间,可得
根据追及问题公式:路程差=速度差×时间,可得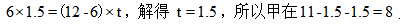 点出发,故此题选择B选项。
点出发,故此题选择B选项。
(2)环形上的相遇与追及
环形上的相遇:环形跑道的周长=速度和×时间(相遇一次所用时间)
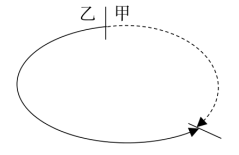
对于环形上的相遇问题,一般题目的题设条件为:甲乙两人在环形跑道的同一地点同时出发背向而行,一段时间后在跑道上的某一点相遇……在此过程中甲乙所行驶的路程之和刚好为环形跑道一圈的周长,时间相等,则环形跑道的周长=速度和×时间。
环形上的追及:环形跑道的周长=速度差×时间(追及一次所用时间)
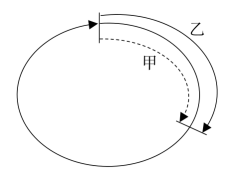
对于环形上的追及问题,一般题目的题设条件为:甲乙两人在环形跑道的同一地点同时出发同向而行,一段时间后在跑道上的某一点两人相遇……在此过程中甲比乙要多走一圈,时间相等,则环形跑道的周长=速度差×时间。
例3
老林和小陈绕着周长为720米的小花园匀速散步,小陈比老林速度快。若两人同时从某一起点同向出发,则每隔18分钟相遇一次;若两人同时从某一起点相反方向出发,则每隔6分钟相遇一次。由此可知,小陈绕小花园散步一圈需要( )分钟。
A.6 B.9 C.15 D.18
【答案】B。【解析】同向出发相当于追及问题,根据环形追及:环形跑道的周长=速度差×时间,二人速度之差为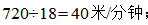 反向出发相当于相遇问题,根据环形相遇:环形跑道的周长=速度和×时间,二人速度之和为
反向出发相当于相遇问题,根据环形相遇:环形跑道的周长=速度和×时间,二人速度之和为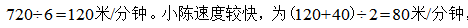 ,散步一圈需要
,散步一圈需要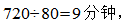 故此题选择B选项。
故此题选择B选项。
以上就是我们相遇追及问题的常见考点及公式,希望广大考生灵活掌握,快速解题。
打破数字推理中的常规思路
数字推理和数学运算是行测数量关系常考的两种题型,不过近几年在国省考当中,更多的是对于数学运算的考查,而数字推理基本就变成了事业单位考查中的“特色”,那么想要攻克数字推理,除了掌握常规的做题思路以外,还需要多多地进行练习,一方面可以增加我们对常规解题思路的熟练程度,从而培养出“数字敏感”和“数列敏感”的两种思维;另一方面也可以多多见到一些非常规考点,从而达到拓展思维、“见多识广”的目的。今天就一起来见一见那些非常规的题目究竟长什么样子。
一、等差数列
例1
108,122,143,165,( )
A.176 B.188 C.192 D.206
【答案】B。【解析】数列单调递增,且从大数字看变化幅度2倍左右,可优先考虑作差。但此题作差并非常规思路,而是需要从第二项起,每一项都减去第一项,得到新数列:14、35、57,再进行作差:
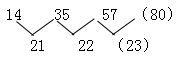 题干应填入108+80=(188)。答案选B。
题干应填入108+80=(188)。答案选B。
例2
168,183,195,210,( )
A.213 B.215 C.223 D.225
【答案】A。【解析】数列单调递增,且从大数字看变化幅度2倍左右,可优先考虑作差:
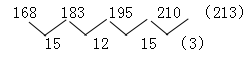 如果按照15、12循环数列规律来计算应为(222),但没有答案,因此需要换种思路把差数列和原数列结合构造网络,即:15=1+6+8,12=1+8+3,15=1+9+5,(3)=2+1+0,题干应填入210+3=(213)。答案选A。
如果按照15、12循环数列规律来计算应为(222),但没有答案,因此需要换种思路把差数列和原数列结合构造网络,即:15=1+6+8,12=1+8+3,15=1+9+5,(3)=2+1+0,题干应填入210+3=(213)。答案选A。
二、和数列
例题
1,3,8,15,( )
A.22 B.26 C.28 D.24
【答案】D。【解析】数列单调递增,整体变化幅度2倍左右,且小数字居多,故考虑作和。但此题加和属于非常规思路,是第一项和后面每一项相加后构成了平方数列。即: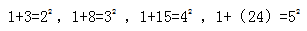 ,故选D。
,故选D。
三、组合数列
例1
2,12,6,30,25,100,( ),( )
A.64,192 B.48,144 C.96,192 D.32,96
【答案】A。【解析】数列较长,总项数≥7项,优先考虑组合数列。将数列两两分组,每组作商后得到6、5、4、(3),即所选的两个数字之间是3倍关系,排除C项;此时规律不易发现,需要换种思路把商数列和原数列结合构造网络去探索就会发现:前一组的商与后一组的第一项构成多次方关系,即: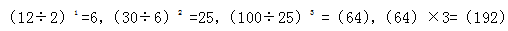 。故选A。
。故选A。
例2
6,24,8,4,20,10,3,6,( )
A.6 B.9 C.12 D.18
【答案】A。【解析】数列较长,总项数≥7项,优先考虑组合数列。将数列中每三个数作为一组,中间的数为两边数的最小公倍数,只有A项符合。
四、数位组合
例题
12,1112,3112,211213,( )
A.312213 B.132231 C.112233 D.332211
【答案】A。【解析】数列具有单调性,从大数字看变化幅度陡增,常规思路易联想到乘积数列或多次方数列,但都无法求解,所以此题规律比较特殊,它是一种规律描述的体现,而非常规的数字计算。即:后一个数是对前一个数的描述,例如:“1112”的意思是:“12”有“1个1和1个2”,依次类推,211213有3个1、2个2、1个3,即312213。故选A。
以上就是行测数字推理中的一些较特殊规律的题目,你掌握了吗?
如何快速解决不定方程问题
数量关系对于大部分考生来说都是行测试卷中难度相对较大的一个部分,而对于其中的题目很多都是采用方程法来解决,利用方程解题的核心在于构造等量关系,在列方程的过程中,会出现一类比较特殊的方程——不定方程,不定方程是指未知数的个数多于独立方程个数的一类方程,它的难点往往在于解方程,那接下来就带着大家一起来学习解不定方程的相关方法。
不定方程的解法一般分为两类,一类是未知数在正整数范围内,通常采用代入排除法、整除、奇偶性、尾数法来解决,另外一类是未知数在任意范围内时,此时采用的方法一般是特值法。下面用例题来具体说明。
例1
某班给学生分发54个苹果,为了保证每人都有,给每个男生分6个,每个女生分5个,正好分完,求有多少个男生?( )
A.8 B.6 C.4 D.5
【答案】C。【解析】由题意,等量关系是男女生所分的苹果总量为54,而想把分到的苹果数量表示出来,还要知道男生和女生各自的人数,所以可以设男女生人数分别为x、y。根据题意,可得6x+5y=54。x、y代表人数,那么一定都是正整数。
方法一,代入排除,把四个选项分别代入到方程中的x,同时要满足y也为正整数,那么只有C满足题意。
方法二,整除法:通过观察方程,我们会发现54为6倍数,6x为6的倍数,则5y也是6的倍数,令y=6,可得x=4,满足题意;令y=12,x为非正整数,不满足题意,随着y不断增大x为负数,不满足题意,故本题选C。
方法三,奇偶性:通过观察方程,我们会发现54为偶数,6x为偶数,则5y为偶数,故y为偶数,令y=2,可得x非整数,不满足题意;令y=4,可得x非整数,不满足题意;令y=6,可得x=4,满足题意;y=8、10均不满足题意,故本题选C。
方法四,尾数法:方程中54尾数为4,5y尾数只能为0或5,又因为54为偶数,6x为偶数,偶数+偶数=偶数,则5y为偶数,故5y尾数只能为0,所以6x尾数为4,令x=4,则y=6,满足题意;令x=9,则y=0,不满足题意,故本题选C。
例2
超市将99个苹果装进两种包装盒,大包装盒每个装12个苹果,小包装盒每个装5个苹果,共用了十多个盒子刚好装完。问两种包装盒相差多少个?( )
A.3 B.4 C.7 D.13
【答案】D。【解析】设大包装盒有x个,小包装盒有y个,则12x+5y=99,其中x、y之和为十多个。5y的尾数只能是5、0,那么对应的12x的尾数只能为4或者9,而12x为偶数,故尾数只能为4。此时,只有x=2或者x=7时满足这一条件。当x=2时,y=15,x+y=17,正好满足条件,y-x=13;当x=7时,y=3,x+y=10,不符合条件,故本题选D。
例3
甲买了3支签字笔、7支圆珠笔和1支铅笔,共花了32元,乙买了4支同样的签字笔、10支圆珠笔和1支铅笔,共花了43元。如果同样的签字笔、圆珠笔、铅笔各买一支,共用多少钱?
A.21元 B.11元 C.10元 D.17元
【答案】C。【解析】根据题意可知,等量关系为两种购买方式所花的钱数已知。那么可以设签字笔、圆珠笔、铅笔的单价分别为a元、b元、c元。根据题意可得3a+7b+c=32①;4a+10b+c=43②,此时a、b、c代表单价,可以是任意范围内,所以求解可以采用特值法,首先令其中一个未知数为0,令b=0,得3a+c=32;4a+c=43,解得a=11,c=-1,故所求a+b+c=11+0+(-1)=10.本题选C。
相信通过上面的几道例题,大家对于不定方程在不同范围内的两类解法也有了一定的了解,而要想真正熟练地掌握这种解法,还需要大家在备考期间多多练习,才能掌握其中的关键技巧,希望对大家的备考有所帮助。
行测利润问题概念杂?列表帮你捋顺它
利润问题是国考行测中的一类常考题型,但往往也是很多考生头疼的题型,之所以利润问题会让人觉得难,是因为其本身所含有的概念较多较杂,导致考生无从下手,今天就带领大家以列表的形式来梳理利润问题当中出现的概念,捋顺它们之间的关系,从而实现快速解题。
一、相关公式

二、例题展示
例1
某品牌代理商2016年以80元/件的价格购进一批毛衫,以200元/件的价格卖出。2017年受市场环境影响,毛衫的进价上涨了30元,售价不变。2017年毛衫的销量比2016年提高25%,但总利润比2016年少了6万元。那么该代理商2017年销售这种毛衫共获利多少万元?( )
A.64 B.90 C.160 D.210
【答案】B。【解析】根据题干信息,设2016年的销量为x件,可列表格

由“总利润比2016年少了6万元”,可得90×1.25x=120x-60000,解得x=8000件,则该代理商2017年销售这种毛衫共获利90×1.25×8000=900000元=90万元,选择B项。
例2
小杂货店买进小杂货店买进一批小球,进价每只1.5元,卖出价每只2元。卖到只剩20只小球时,开始让利,以9折售出。小球全部卖完后,共得利润86元。这批小球的总数是多少?( )
A.160只 B.180只 C.200只 D.220只
【答案】B。【解析】根据题干信息,设以原价卖了x只,可列表格

由“小球全部卖完后,共得利润86元”,可得0.5x+6=86,解得x=160只,则这批小球的总数是160+20=180只,选择B项。
例3
某书店开学前新进一批图书,原计划按40%的利润定价出售,售出80%的图书之后,剩下的图书打折促销,结果所得利润比原计划少14%,则剩下的图书销售时按定价打了几折?( )
A.7 B.7.5 C.8 D.8.5
【答案】C。【解析】根据题干信息,设这批图书成本为x,总量为y,打折率为z,可列表格

由“所得利润比原计划少14%”,可得0.4x×0.8y+(1.4x×z-x)×(0.2y)=0.4xy×(1-14%),解得z=80%,即剩下的图书销售时按定价打了8折,选择C项。
通过以上例题,相信各位考生能够很直观地感受到用表格梳理利润问题的优势,所以以后在此类问题中建议大家养成良好的列表习惯,在求解利润问题时才能做到事半功倍。








