行测数量关系瓶和水、牛吃草、利润问题解题技巧

行测“新宠”瓶和水的问题，你知多少？

近年来，统筹问题已成为行测考试中的“新宠儿”。在我们的日常生活和工作中也经常会遇到物资调配、合理分配、排队、操作等问题。面对这类问题如何才能合理安排，怎样才能更快、更有效地办事，这就是要在统筹问题中所要解决的。空瓶换水问题作为统筹问题中的一类，经常让各位考生因抓不住解题的关键而抓狂。今天给大家介绍这样的一个小窍门——“水是水，瓶是瓶”，来解决空瓶换水问题。

一、什么是空瓶换水问题？

空瓶换水，指的是给出n个空瓶可以换m瓶水这个规则，问考生买几瓶水最多可以喝到多少水或者想喝一定数量的水最少需要自己购买几瓶等类似的问题。

示例

某便利店销售每瓶1元的矿泉水，老板举办活动5个空瓶可换1瓶矿泉水，问小明用100元最多可以喝到多少瓶水？（   ）

A.120     B.123      C.124      D.125

二、难点及方法

上题中很容易犯的错误是100元购买100瓶水喝完后，100个空瓶按照每5个换1瓶水计算，100÷5=20，错选为A，但题目要求是最多可以喝到多少水，发现换到手的20瓶水喝完，就又有了20个空瓶，此时可以继续兑换出20÷5=4瓶水，再喝完得到4个空瓶，此时不够5个就无法兑换，又错选了C。但是4个空瓶可以向老板借1个瓶子换1瓶水，然后喝完把空瓶再还回去，因此最多实际可以喝到100+20+4+1=125瓶水。其中的难点主要是多次兑换和先借后还两方面，为避免在考虑多个过程中出错，我们可以从交换规则入手，5个空瓶=1瓶水=1空瓶+1份水，即4空瓶=1份水，100元可买100瓶水即100空瓶+100份水，100空瓶又可得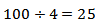份水，则最多可喝100+25=125份水，选D。所以解决空瓶换水问题只需将水与瓶分开考虑，弄清楚水与瓶的交换规则即可。

三、考法

1.直接套用公式：已知规则及空瓶数，求最多能喝到的水数。

示例

若12个矿泉水空瓶可以免费换1瓶矿泉水，现有101个矿泉水空瓶，最多可以免费喝到几瓶矿泉水？（  ）

A.8瓶     B.9瓶     C.10瓶     D.11瓶

【答案】B。【解析】“12个矿泉水空瓶可以免费换1瓶矿泉水”，即12空瓶=1空瓶+1水，可得11空瓶=1水，所以101空瓶最多能免费喝到的水瓶，选B。

若在“12个空瓶换5瓶水”的规则下，问101个矿泉水空瓶，最多可以免费喝到几瓶矿泉水？即12空瓶=5空瓶+5水，可得7空瓶=5水，所以最多能免费喝到的水数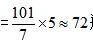瓶。

2.间接用公式：已知规则及喝到的水数，求至少应买多少瓶水。

示例

六个空瓶可以换一瓶汽水，某班同学喝了213瓶汽水，其中有一些汽水是用喝完后的空瓶换来的，那么他们至少要买多少瓶汽水？（   ）

A.176瓶    B.177瓶    C.178瓶     D.179瓶

【答案】C。【解析】根据题意可知：六个空瓶可以换一瓶汽水，即5空瓶=1份汽水，假设他们至少买了汽水x瓶。则换回的汽水份数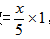，根据题意有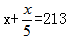，解得x=177.5。所以他们至少要买178瓶汽水，故选择C选项。

总结：在行测考试中，各位考生在遇见空瓶换水问题时，只需将空瓶换水的规则按水与空瓶分开去看便可解决问题，希望通过今天的分享能为各位考生在备考路上添砖加瓦。

三种方法攻克利润问题

在近些年公务员考试行测中，利润问题考查频率高，备受考官青睐。但对于备考的同学来说却为之头大。此类题型概念虽多往往简单易懂，是考试中的得分点，因此做好这类题是关键。接下来给大家主要讲讲如何用三种方法攻克利润问题，你准备好了吗？那我们一起来学习吧。

方法一：公式法 

对于大部分的利润问题只需要审清题干，再结合基本公式就可以解决。

例1

某电商一款手机的进价是每台5000元，卖掉后每台手机的利润是2000元，现在由于出了新款手机，进价成本降低，商家将手机9折出售，但毛利润比过去增加了20%，则现在每台手机的进价是多少元？（  ）

A.4500      B.4200    C.3900    D.3600

【答案】C。【解析】题目当中所求为进价即成本，根据公式：利润=售价-成本，可知：成本=售价-利润，只需要计算出售价、利润即可，则现在的售价为(5000+2000)×0.9=6300元；毛利润为2000×(1+20%)=2400元，因此现在每台手机的进价为6300-2400=3900元。故选择答案C。

方法二：方程法 

利润问题中，部分题目可能会存在成本或者原价未知，不能直接用公式求解，需要设未知数，找到等量关系列方程进行求解。对于未知量，可设为x。

例2

张先生向商店订购了某种商品80件，每件定价100元。张先生向商店经理说：“如果你肯减价，每减1元，我就多订购4件。”商店经理算了一下，如果减价5%，由于张先生多订购，仍可获得与原来一样多的利润。则这种商品每件的成本是(    )。

A.75元     B.80元     C.85元     D.90元

【答案】A。【解析】设该商品每件成本x元，则未减价前每件利润为(100-x)元，减价5%后每件利润为(95-x)元，订购数量为(80+5×4)件，根据题意有80×(100-x)=(80+5×4)×(95-x)，解得x=75。故答案选A。

方法三：特值法 

在利润问题中，当有些题目具体已知量较少，且题干的已知信息大部分为分数、百分数、折扣等时，可以将某一些量设为特殊值，方便我们求解。即为特值法。

例3

一批商品按期望获得50%的利润来定价，结果只销售掉70%的商品，为尽早销售掉剩下的商品，商店决定按定价打折出售，这样所获得的全部利润是原来所期望利润的82%，问打了多少折扣？（  ）

A.4折     B.6折      C.7折      D.8折

【答案】D。【解析】设每件成本为100元，商品一共有10件，打x折，则有：

根据“所获得的全部利润是原来所期望利润的82%”，可得(150-100)×7+(150x-100)×3=(150-100)×10×82%，解得x=0.8，即打了8折。故答案选D。

从以上例题不难看出利润问题难度不大，大家需要记住基本公式利用公式法，再结合方程法和特值法，便能快速求解利润问题。希望大家多加练习，一定能使行测更上一个台阶。

神秘的牛吃草问题

牛吃草问题广泛存在于行测考试数学运算部分的题目中，对于这一问题，许多同学往往会感到题目理解比较困难，花费的时间很多，但是真正能够解决的牛吃草问题很少，甚至干脆放弃这部分题目。今天就带大家一起，揭开牛吃草问题的神秘面纱，掌握做题思路，化繁为简。

一、例题展示

①一片牧场上的青草每天匀速生长，牧场上的草如果28头牛可以吃6天，如果21头牛吃可以吃9天。那么牧场上的青草可供13头牛吃几天？

②由于天气逐渐变冷，牧场上的草每天以均匀的速度减少。经计算，牧场上的草如果6头牛吃可以吃12天，如果8头牛吃可以吃10天。那么牧场上的青草可供11头牛吃几天？

二、题目特征总结 

通过以上两到例题，我们可以将牛吃草问题的题目特征进行总结：

特点(一)：原有草量是固定的；草量受两个因素制约：一是草每天匀速生长(减少)，使草量增加(减少)，二是牛吃草使草量减少；

特点(二)：题目中大量使用排比句式：如果……如果……。

因此满足以上两种特征的题目，我们就可以将其归类为牛吃草问题。

三、题型分类 

牛吃草问题可以大体分为三类题型即：夏天(追及)型牛吃草，冬天(相遇)型牛吃草，极值型牛吃草。今天我们主要学习第一类。

四、解题思维及方法精析 

对于夏天型牛吃草问题，我们可以从上文提到的例题一入手。可以把草原想象成一条线段，所有的牛排成一列沿着草原线段的左边端点开始向右侧吃草，生长的草是从草原线段的右端点统一向右生长，此时可以相当于牛和草两个运动物体，以草原线段为初始距离，展开一场追及过程，因此就可以利用追及公式，将该模型进行转化。具体如下：

将草原原有草量设为M，将草生长速度设为x，每头牛单位时间吃草的量为1，数量为N，吃草的时间为t，则夏天型牛吃草的公式就可以总结为：

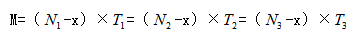
后续做题中我们只需要将题目中所给的数据带入到以上式子中即可。

五、试题精析 

例1

一片牧场上的青草每天匀速生长，牧场上的草如果28头牛可以吃6天，如果21头牛吃可以吃9天。那么牧场上的青草可供13头牛吃几天？

【解析】假设可供13头牛吃t天，则有M=(28-x)×6=(21-x)×9=(13-x)×t，解得x=7，M=126，t=21，故可供13头牛吃21天。

例2

省博物馆每日9点开馆，有大量观众前来参观，很早就有人排队等候入场，假设从第一个观众到来起，每分钟来的观众人数一样多，每个入场口进入的速度是一样的，如果开放5个入场口，则9点20分就不再有人排队，如果设6个入场口，则9点15分就没有人排队，那么第一个观众到达时间是：（   ）

A.9时                B.8时45分

C.8时30分                  D.8时15分

【答案】C。【解析】假设每个入场口每分钟只能进1人，每分钟来的观众数为x人，则有(5-x)×20=(6-x)×15，解得x=2人，九点时到场观众数(5-2)×20=60人，60÷2=30分钟，故第一个观众到达时间是8时30分。选C。