
行测数量关系备考技巧
不定方程如何定选项
行测备考中数量关系尤为重要,因为它确实有一定的难度。而在行测考试中,数量关系单题分值很高,特别在国考副省级考试中,数量关系题量也比较大,是相当具有区分度的一个科目,所以需要学。而高效的学习,绝不能闭门造车,需要根据科学的学习方法,把握其中的技巧。本次为大家介绍一个重要考点——解不定方程,方程思想是在考试中多次体现,而不定方程,相较于普通方程,考生会更加陌生。
一、认识不定方程
未知数个数大于独立方程数。
例:3x+2y=15
二、解不定方程
在实数范围内,x任意取值,都会有满足方程的y,因此有无数组解。而在实际问题中,往往在正整数范围内求解,再结合题目限制条件,就会是有限组解。解不定方程的思路,有以下几类:
1.代入排除法
例1
6x+7y=133,已知x,y为正整数,则y可能为( )
A.5 B.6 C.7 D.8
【答案】A【解析】代入A项,原式化为6x+7×5=133,解得x非正整数,A排除;代入B项,原式化为6x+7×6=133,解得x非正整数,B排除;代入C项,原式化为6x+7×7=133,解得x=14,满足题意,故本题选C。
2.整除特性
一般用于未知数系数与和(差)存在非1的公约数时,则通过所有项均能被该公约数所整除进行求解。
例2
7x+4y=48,已知x,y为正整数,则x=( )
A.3 B.4 C.5 D.6
【答案】B【解析】4y和48都能被4整除,则7x能被4整除,即x能被4整除,选B。
3.奇偶性
一般用于未知数系数为一个奇数和一个偶数时,可通过确定每一项奇偶性进行求解。
例3
3x+2y=40,已知x,y为质数,则y-2x=( )
A.10 B.11 C.12 D.13
【答案】D【解析】2y为偶数,40为偶数,则3x为偶数,由于x为质数,故x只能为2,解得y=17,故y-2x=17-2×2=13,选D。
4.尾数法
一般用于未知数系数的尾数为0或5时,通过确定每一项的尾数进行求解。
例4
5x+8y=31,已知x,y为正整数,则x+y=( )
A.5 B.6 C.7 D.8
【答案】A【解析】8y为偶数、31为奇数,则5x为奇数,故5x的尾数只能为5,8y的尾数为6,当y=2时,x=3,则x+y=3+2=5,选A。
三、实战演练
例5
甲乙丙丁四位小朋友的年龄之和为25岁,按照年龄从大到小排序分别为甲乙丙丁。已知甲的年龄是乙和丙的年龄之和,乙的年龄是丙和丁的年龄和。则甲的年龄为( )岁。
A.8 B.9 C.10 D.11
【答案】D【解析】设丙的年龄x岁,丁的年龄为y岁,则x>y,乙的年龄为x+y,甲的年龄为x+y+x=2x+y,故(2x+y)+(x+y)+x+y=4x+3y=25,由于4x为偶数,25为奇数,故3y为奇数。当y=1时,x不是整数;当y=3时,x=4符合要求,此时甲的年龄为4×2+3=11岁。选A。
以上就是不定方程的解法,分析等量关系列出不定方程,再找到合适的方法求解,总体不难。其实,行测的技巧还有很多,许多题目都可以列方程求解。希望考生可以克服对数量关系的恐惧,举一反三。
擅用整除,加快速度
在公务员考试中行测往往是决定考生分数的主要科目,然而数量关系知识点繁多复杂,分值虽高但是让很多考生望而却步,那么在短时间内如何有效利用时间,并且获得自己满意的分数呢?那么今天就跟各位一起探讨一种既能快速锁定答案,又能保证准确度的方法:整除。学习好它讲在考试中发挥的巨大作用。
一、整除的应用题型
1.文字体现整除:当题目中出现平均、每、倍数、整除这些字眼即可考虑整除。
例题
学校组织春游,每四个人一条船,刚好坐满;但是如果每六个人一条船,则最后一条船少两个人。问春游的学生共有多少人?( )
A.120 B.122 C.124 D.126
【答案】C【解析】题目中出现了倍数的关系,所以我们可以考虑整除的方法去求解。问题中所求为春游的学生数,已知每4人一条船正好坐满,意味着人数可以被4整除,代入选项,排除b.d。根据题意可以判断总人数是6的倍数少两人,所以原人数加2是6的倍数,代入a选项120+2=122,不能被6整除所以排除。只有C选项符合题意。
2.数据体现整除:当题目中出现分数、百分数、小数、比例时考虑整除法。
例题
某次英语考试,机械学院有210人报名,建筑学院有130人报名。已知两个学院缺考人数都相同,机械学员实际参加考试的人数是建筑学院实际参加考试人数的13/8,问建筑学院缺考的人数是多少?( )
A.2 B.4 C.9 D.12
【答案】A【解析】题目中出现了分数,所以可以利用整除思想。由机械学院实际参考的人数是建筑学院实际参考人数的13/8,可知建筑学院实际参加考试的人数能被8整除。结合分析,参加考试的人数为总人数130减去缺考人数能被8整除,代入选项,将130减各个选项只有选项A满足被8整除。
二、常见的小数字整除判定
通过上题我们明确了整除的应用,但是在计算整除时可能会浪费时间,接下来我们去看一下一些常见的小数字整除判定,更加节省时间。
(1)从局部看:
2、5看这个数字的末一位。
4、25看这个数字的末两位。
8、125看这个数字的末三位。
(2)从整体看:3、9把这个数字中各个数位的数字加和,和能够被3或9整除即可。
(3)需分段看:7把这个数字分成两个部分,后三位和剩余部分,用剩余部分减去后三位,绝对值能够被7整除即可。
(4)合数判断:6、15、18等,把合数分解成互质的数,满足被所有的质因数整除即可。
以上就是给大家介绍的整除方法,可以大大节省我们的计算量,缩短计算时间。未来我们也要多使用、多整理、多思考这种方法。
“定位法”巧解概率问题
在行测考试中,数量关系是必考内容之一。但是,对于众多考生来说,大家都认为数量关系比较难,考试时间不够,难以在考场完成,考试时常常放弃,直接蒙选项。其实在考试中还是有很多题目,只要我们掌握了常见的方法,并通过练习巩固这类题目的常考题型,在考试时解决这类题目还是相对简单的。下面我们带大家一起来学习如何利用“定位法”解决概率问题。
概率的含义
概率是指随机事件发生的可能性大小。而在国考和省考中,概率问题常考的是古典概率。古典概率的计算公式:
P(A)=A事件包含的等可能样本数/总事件包含的所有等可能样本数
“定位法”是解决古典概率问题中的一种方法,就是先将其中一个元素“固定”,再求另一个元素也发生这件事情的概率,同样符合古典概率的计算公式。
实际应用
能用“定位法”的题目,题干描述中往往会出现两个相关联的元素,最后求它们共同发生某件事的概率。下面我们就通过3道例题来学习这种方法:
例1:某电影院共有五排共30个座位,每排座位数相同,小张和小李随机入座(2人不在同一座位),则这2人坐在同一排的概率:( )
A.小于等于15% B.大于15%但小于20%
C.正好为20% D.大于20%
【答案】B【解析】方法一:题目要求2人随机入坐到30个座位中,故总事件包含的所有等可能样本数有 个。题目描述五排共有30个座位且每排座位数相同,则每排有6个座位。所以可先确定五排中的任意一排,再让2人从同排的6个座位中选2个入座,则事件A包含的等可能样本数有
个。题目描述五排共有30个座位且每排座位数相同,则每排有6个座位。所以可先确定五排中的任意一排,再让2人从同排的6个座位中选2个入座,则事件A包含的等可能样本数有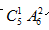 个。所以概率为:
个。所以概率为: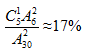
方法二:我们知道五排共有30个座位且每排座位数相同,则每排有6个座位。现在要将2人关联在一起安排到同一排,符合定位法的应用环境。我们可以先从30个座位中任选1个固定为小张的座位,此时还剩下29个空座位。若想2人在同一排,小赵只能挑选小张所在的这排中剩余5个座位中的1个,则2人在同一排的概率为: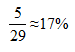
例2:某单位举办象棋比赛,共有6人报名,随机分成3组,每组2人。那么,小王和小李恰好被分在同一组的概率为:
A.1/3 B.1/5 C.1/6 D.1/15
【答案】B【解析】这道题要将小王和小李两个人关联在一起分到同一组去完成比赛,符合定位法的应用环境。题干中描述有6人参加比赛意味着就会有6个位置,若我们先从6个位置中任选一个固定为小王的位置,此时还剩5个位置可以安排小李。若想和小王在同一组,则小李只能选择小王旁边唯一的位置。
故所求概率为:1/5。
例3:小红有4双相同的鞋子放在一个大箱子中,随机拿出2只,恰好组成一双的概率为:( )
A.1/4 B.1/7 C.1/8 D.4/7
【答案】D。
【答案】这道题要将两只鞋关联在一起组成一双,符合定位法的应用环境。题干中描述有4双相同的鞋(4只相同的左脚和4只相同的右脚,共8只),若我们先选一只是左脚鞋,此时还剩7只鞋可选。若想与所选的左脚鞋组成一双,则只能选择4只右脚鞋中的1只。
故所求概率为:4/7。
相信大家只要熟练掌握这三道例题,清晰地认识“定位法”的含义和应用环境,在日常学习中加以练习,这样的题目就能迎刃而解。
行测数量关系盈亏思想的基本解题思路
盈余亏补思想是指多的量和少的量保持平衡的思想。在行测数量关系题目中,很多时候我们会利用等量解题,但有时解方程又影响做题速度,如果使用盈亏思想去解题,可以为我们简化计算的难度,提高我们做题效率。下面为大家带来三种盈亏思想的基本解题思路,配合例题让大家体会一下盈亏思想。
一、解盈亏问题的基本思路
1.总盈亏数÷单个盈亏数=数量
2.盈亏总数之差÷分配数之差=分配组数
3.总盈数=总亏数
二、方法应用
例1:小明负责将某农场的鸡蛋运送到小卖部。按照规定,每送达1枚完整无损的鸡蛋,可得运费0.1元;若有鸡蛋破损,不仅得不到该枚鸡蛋的运费,每破损一枚鸡蛋还要赔偿0.4元,小明10月份共运送鸡蛋25000枚,获得运费2480元,那么,在运送过程中,鸡蛋破损了多少枚?( )
A.20枚 B.30枚 C.40枚 D.50枚
【答案】C【解析】每枚完整无损的鸡蛋,得运费0.1元,每一枚鸡蛋破损,不仅得不到该枚鸡蛋的运费,还要赔偿0.4元,可理解为每枚坏鸡蛋比完整的蛋少获得了0.1+0.4=0.5元,那么25000枚鸡蛋如果均是完好无损的,则理论上可获得25000×0.1=2500元,比实际获得的2480元少了20元。可得共有坏鸡蛋20÷0.5=40枚。选C。
这题中我们可以看到,总亏数(实际有坏鸡蛋比全为好鸡蛋少得金额)为少了20元,单个亏数(单个坏鸡蛋比好鸡蛋所少金额)为0.5元,两者相除就是坏鸡蛋数量。
例2:食堂采购员小李到集贸市场去买肉,如果买牛肉18千克,则差4元;如果买猪肉20千克,则多2元。已知牛肉、猪肉每千克差价8角。问小李带了多少钱?( )
A.86元 B.72元 C.64元 D.56元
【答案】A【解析】这里有两种肉,思考起来比较困难,能否化为一种肉的问题呢?仔细分析一下已知条件,买牛肉18千克差4元,而买猪肉20千克还多2元,说明牛肉贵一些。而且每千克贵8角,如18千克牛肉换成18千克猪肉,就要少花8×18=144(角)=14元4角。这样就会多出14元4角-4元=10元4角。因此问题就可变为:“小李买猪肉18千克多余10元4角,买20千克多余2元,求有多少钱”。
这就转换为了最基本的盈亏思想,猪肉单价=两次盈余钱的差÷两次千克量差。
所以猪肉每千克价格为(104-20)÷(20-18)=84÷2=42(角)=4元2角;小李带的钱为:4.2×20+2=86元。选A。
例3:甲乙合作工程24天完成,如甲做6天,乙做4天,完成工程的1/5,问单独完成此工程甲乙各需多少天完成?( )
A.30,50 B.40,60 C.50,30 D.60,40
【答案】D。这项工程由甲乙合作工程24天完成,可看做甲乙两人各做24天完成。此外甲做6天,乙做4天完成总工程的1/5,说明按照这种工作方式,完成该工程需要甲做6×5=30天,乙做4×5=20天。相比之下甲多工作了6天,乙少工作了4天。根据总盈数=总亏数,则甲6天工作量等于乙4天工作量,可将合作24天中甲24天的工作量转化为乙16天的工作量,则乙单独完成该工程需要24+16=40天。同理甲单独完成需要60天。选D。
以上三道例题可以帮助大家对盈亏思想有一个直观的认识和感受,当题干中出现盈亏相关条件,也就是将一定总量的事物,按照不同方案分配,造成不同的结果。比如例1的25000枚鸡蛋,分为不同数量的好鸡蛋和坏鸡蛋,得到运费不同;例2中小李手里的钱,购买不同方案的肉类,所剩(差)的金额不同;例3中的这项工程,不同的工作方案,所需时间不同。这一类条件均可看做盈亏的条件,从而使用盈亏思想解决问题。
其实盈亏思想也可运用到各种题型之中,如鸡兔同笼,工程问题,行程问题,利润问题等,在做题中不妨思考可否用盈亏思想去进行解题。








