行测数量关系备考指导
行测指导：如何区分分类与分步以及排列与组合
排列组合类问题是行测试卷中考察难度相对较大的一部分，其中最基础最核心的问题是如何去分清楚谁是分类(用加法计算情况数)谁是分步(用乘法计算情况数)，以及什么时候用排列数计算什么时候用组合数计算。那在做题过程中，到底该怎样区分清楚这些相近的概念？接下来带大家来了解此类问题的区分方法，从而解决排列组合类的常规问题。
问题一：如何区分分类与分步？
分类：在解决一个问题时，分成几类不同的情况。每一类情况都能完成这件事。
分步：在解决一个问题时，分成几个步骤去做。需要把每一步都做完，才能完成这件事。
区别：能否独立完成这件事。
例1
①考核方式有两种，参加射击考核或者是格斗考核。射击考核的方案有两种，格斗考核的方案有三种。问：参加考核的总方案有多少种？
【答案】考核方式分两种，无论是参加射击考核还是参加格斗考核，都算作参加了考核，都完成了考核这件事。所以是把考核方式分成了两类，每一类情况都能完成这件事，即为分类，用加法。方案数为2+3=5。
② 考核共有两场：射击考核和格斗考核。射击考核的方案有两种，格斗考核的方案有三种。问：参加考核的总方案有多少种？
【答案】考核共分两场，无论是只参加射击考核还是只参加了格斗考核，都没有把考核这么一件事给做完。所以应该是分步骤去做的。可以先参加其中一项考核(比如射击考核)，再参加另一场考核。把这两场考核都考完才算完成了考核这么一件事。分步用乘法。方案数为2×3=6。
问题二：如何区分排列与组合？
从N个不同的元素中选M个元素出来。有顺序要求的称之为排列。没有顺序要求的称之为组合。
区别：有无顺序要求。
判断方法：调换顺序后，看情况是否对结果有影响。
例2
①从8名战士中选2人参与考核，问：方案数有多少种？
【答案】假设选择的是甲乙两人。那么调换顺序后选择的应该是乙甲两人。但无论是甲乙还是乙甲都是这两个人参与考核，没有区别，所以是组合。方案数为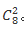
。
②从8名战士中选2人分别参与射击和格斗考核。问：方案数有多少种？
【答案】假设选择的2人是甲参加射击考核，乙参加格斗考核。调换顺序之后，甲参加格斗考核乙参加射击考核。两种情况有区别，所以有顺序要求，是排列。方案数为：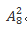
。
相信大家通过上述题目的讲解，能对如何区分排列组合类问题的分类与分步，排列与组合有所了解。建议大家在备考期间需多多练习，真正做到熟练掌握这类问题，希望对于大家的备考能有所帮助。
行测难点：看看谁更擅长——多劳力合作
行测备考过程中，工程问题算是大家的“老熟人”了。工程问题中一类题型——多劳力合作却有些棘手。接下来带大家来认识一下多劳力合作问题，学一学应对之道。
一、解题关键
多劳力合作的关键是合理分工，合理分工就是分析谁更擅长。
二、解题原则
1.分析更擅长的方法是比较效率比，取大值的分子。
2.分析更擅长的方法也可以比较时间比，取小值的分子。
3.求最大工作量，让先做完的按比例分配时间。
4.求最短时间，让先做完的和慢的一起完成剩下的。
三、实际应用
例1
小王和小刘手工制作一种工艺品。每件工艺品由一个甲部件和一个乙部件组成。小王每天可以制作150个甲部件，或者制作75个乙部件；小刘每天可以制作60个甲部件，或者制作24个乙部件。现两人一起制作工艺品，10天时间最多可以制作该工艺品( )件。
A.660 B.675 C.700 D.900
【答案】C。【解析】如下表所示：不论是甲部件还是乙部件，都是小王的生产效率高。由于制作甲、乙部件的效率比有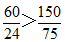
，则应小刘效率取60即全部生产甲部件，而小王负责使部件配套。
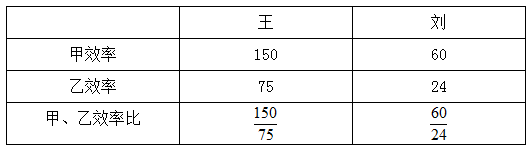
小刘10天共做60×10=600个，小王做600个乙部件用600÷75=8天，则剩下2天小王按比例分配时间用
天制作乙部件，共制作
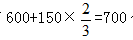件该工艺品。本题选择C项。
【总结1】分析更擅长的方法是比较效率比，取大值的分子；且求最大工作量，让先做完的按比例分配时间。
例2
有甲、乙两项工程，张师傅单独完成甲工程需6天，单独完成乙工程需30天，李师傅单独完成甲工程需18天，单独完成乙工程需24天，若合作两项工程，最少需要的天数为：（ ）
A.16 B.15 C.12 D.10
【答案】A。【解析】如下表所示：张师傅与李师傅两人在不同工程的效率不同，需要考虑工程分配问题。由于张、李时间比有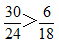
，张师傅先做甲工程，李师傅先做乙工程，张师傅先用6天完成甲工程，之后再与李师傅一块完成乙工程。
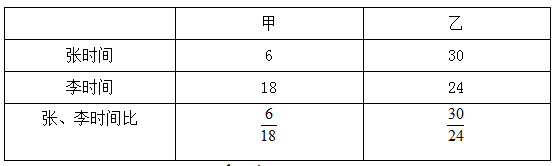
李师傅6天完成乙工程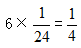
，余下的张师傅与李师傅一起合作需要
。本题选择A项。
【总结2】分析更擅长的方法也可以比较时间比，取小值的分子；且求最短时间，让先做完的和慢的一起完成剩下的。
相信通过以上的学习，能够帮助各位考生清晰了解多劳力合作中“谁更擅长”的问题，也希望大家在之后备考过程中勤加练习，熟练应用，面对此类问题可以冷静分析沉着应对！
行测备考：如何破解多者合作问题
在行测考试中，数量关系一直是很多考生觉得有些困难且难以克服的部分。但其中也有部分题目掌握技巧后容易上手，可加强这些题型的熟练度，比如多者合作问题。接下来带大家一起看看多者合作问题的常见考法。
一、多者合作问题
多者合作问题是多个人一起完成一项或者多项工作的工程问题。
二、基本公式：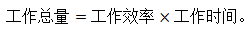
三、解题核心：合作效率等于各个部分的效率之和。
四、解题方法
在计算复杂的问题中，常通过设题目中工作总量、效率等为特殊值，进而达到简化计算的目的，这种方法叫做特值法。常有如下考法：
1.已知多个工作时间时，一般设工作总量为特值，可设为工作总量为“时间们”的最小公倍数，进而表示出工作效率。
2.已知工作效率比例关系，一般直接将工作效率设为最简比，进而表示出工作总量。
3.已知效率相同的多个主体合作，往往将一个个体的单位时间内的工作量设为1，即直接用个体的数量代表工作效率。
五、例题精讲
1.已知多个工作时间时，一般设工作总量为特值：可设为工作总量为“时间们”的最小公倍数，进而表示出工作效率。
例1
甲乙两个水管单独开，注满一池水，分别需要20小时，15小时。丙水管单独开，排完一池水要12小时。若水池没水，同时打开甲乙两水管，4小时后，再打开排水管丙，问水池注满还需要多少小时？（ ）
A.10 B.12 C.15 D.16
【答案】D。【解析】设工作总量为时间的最小公倍数60，故进水管甲的效率为3，乙的效率为4，排水管丙的效率为-5。则4小时后，甲乙做的工作总量为4×(3+4)=28，还余下60-28=32的工作总量，再由甲乙丙合作需要32÷(3+4-5)=16小时。故本题选D。
2.已知工作效率比例关系，一般直接将工作效率设为最简比，进而表示出工作总量。
例2
甲、乙两人共同完成一项工程需要10天，甲的效率是乙的3倍。如果甲的效率保持不变，乙的效率提高一倍，且乙在中途休息了2天，问要保证工作按照原来的时间完成，则甲休息几天？
A.1 B.2 C.3 D.4
【答案】B。【解析】已知甲乙的效率之比为3：1，可设甲的效率为3，乙的效率为1，则工程总量为(1+3)×10=40。乙的效率提高一倍之后为2，且乙在中途休息了2天，若要保证工作按照原来的时间完成，则乙工作的时间为8天，故乙完成的工程总量为2×8=16，因此，甲工作的时间为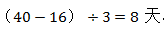
。所以甲休息了10-8=2天。故本题选B。
3.已知效率相同的多个主体合作，往往将一个个体的单位时间内的工作量设为1，即直接用个体的数量代表工作效率。
例3
修一条公路，假设每人每天的工作效率相同，计划180名工人1年完成，工作4个月后，因特殊情况，要求提前2个月完成任务，则需要增加工人多少名？（ ）
A.50 B.65 C.70 D.60
【答案】D。【解析】设每名工人每个月的工作量为1，故余下8个月的工作量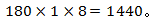
剩下的这些工作量需要6个月完成，故需要
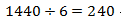名工人，所以要增加 240-180=60名工人。故本题选D。
以上为工程问题特值法的做法分享。不积跬步，无以至千里；不积小流，无以成江海。提醒各位同学注意多加练习三种题型，提高熟练度！
行测备考：年龄问题你会了吗？
数量关系是行测考试中的重要部分，大部分考生都认为在考试时间有限的情况下难度比较大，不会做。其实也有简单的题，比如年龄问题整体难度不大，解题核心单一，在备考中建议考生熟练掌握。接下来带大家学习解决年龄问题的核心及方法。
一、什么是年龄问题
年龄问题是研究两人或者多人之间的年龄变化和关系的问题。
二、年龄问题的核心
1.年龄同增同减：每过一年，所有人都增长一岁。
2.年龄差不变：每过N年，每个人的年龄均增长N岁，也就是任意两人的年龄差不变。
三、常用方法
1.方程法：题干描述比较简单，等量关系比较明显。
2.列表法：题干描述比较复杂，等量关系不太明显。
例1
办公室有甲、乙、丙、丁4位同志，甲比乙大5岁，丙比丁大2岁。丁三年前参加工作，当时22岁。他们四人现在的年龄之和为127岁。那么乙现在的年龄是( )。
A.25岁 B.27岁 C.35岁 D.40岁
【答案】C。【解析】设乙现在的年龄是x岁，则甲现在的年龄是x+5 岁，丁现在25岁，丙现在27岁，则有x+5+x+27+25=127，解得x=35，所以乙现在的年龄是35岁。选择C选项。
例2
3年前张三的年龄是他女儿的17倍，3年后张三的年龄是他女儿的 5倍，那么张三的女儿现在：（ ）
A.2岁 B.3岁 C.4岁 D.5岁
【答案】D。【解析】设女儿现在的年龄为x岁，列表如下：
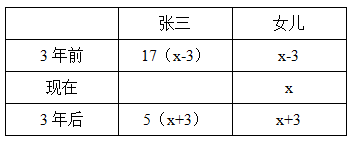
根据张三和女儿的年龄差不变，有17(x-3)-(x-3)=5(x+3)-(x+3)，解得x=5，则女儿现在的年龄为5岁。选择D选项。
通过以上例题，我们知道年龄问题解题核心也就是年龄同增同减、年龄差不变，在做题过程中，简单题型可以直接通过方程法构建等量关系解题，复杂题型可以通过列表法梳理各个人物不同年份年龄之间的关系，结合方程法构建等量关系解题，大家掌握了吗？
