行测数量关系之备考技巧
行测数量关系之苹果与抽屉的爱恨情仇
在行测考试中，数量关系一直都是令各位小伙伴最头疼的问题，因其难度较大，所以导致很多人甘愿放弃，也有不少考生在出考场之后笑谈：数量题的每个字我都看得懂，但是连起来我就不明白了。其实数量关系中的一些问题是需要通过前期的积累。今天就一起来看一下数量关系中的抽屉原理，了解一下这类问题该怎么解决。
抽屉问题又叫狄利克雷原理，他可以解决很多有趣的问题。我们先从最简单的问题说起，比如：将三个苹果放入到两个抽屉中，想一想每个抽屉的情况是怎样的？要么是一个抽屉里放两个苹果，而另一个在第二个抽屉；要么是三个苹果都放一个抽屉中。而这些情况总结一下就是有一个抽屉至少会放两个苹果。
如果我们把上一个问题改一下，改成十个苹果放入九个抽屉中呢？我们不难发现，这十个苹果无论怎么放，仍然会有一个抽屉至少放了两个苹果。
下面一起来看一下抽屉原理的定义：若把多于n件物品放入n个抽屉中，则一定有一个抽屉的物体数不少于2件；若有多于m×n个物品放入n个抽屉中，则一定有一个抽屉中的物品书不少于m+1件。
我们一起来用抽屉原理解决几个问题
例1：篮子里有苹果、梨、桃和橘子，现有81个小朋友，如果每个小朋友都从中任意拿出两个水果，那么至少有多少个小朋友拿的水果是相同的（ ）
A.9 B.6 C.10 D.8
【答案】A【解析】首先应弄清谁是“苹果”谁是“抽屉”。这里相当于将81个朋友放进不同的水果搭配中。所以小朋友就是“苹果”，水果搭配是“抽屉”。所以先求出不同的水果搭配有多少种，拿出的两个水果相同的情况有4种；两个水果不同的情况有6种：苹果和梨、苹果和桃、苹果和橘子、梨和桃、梨和橘子、桃和橘子。所以不同的水果搭配共6+4=10种。将这10种情况视为10个“抽屉”。81÷10=8……1，根据抽屉原理，至少有8+1=9个小朋友拿的水果相同。本题选A。
例2：学校开了语文、数学和美术三种课外班，每个学生最多可以参加两个(可以不参加)。问：至少有多少个学生，才能保证有不少于5学生名参加课外班的情况完全相同？（ ）
A.28 B.29 C.30 D.31
【答案】B【解析】首先弄清楚谁是“苹果”谁是“抽屉”。这里相当于将学生放到不同的课外班搭配中，所以学生是“苹果”、课外班搭配是“抽屉”。所以先求出不同的课外班搭配情况，都不参加的情况有1种；参加一个的情况有3种；参加两个的情况有3种：语文数学、语文美术、数学美术。所以不同的课外班搭配是1+3+3=7种。将这7种情况视为抽屉数，根据抽屉原理，要求不少于5名参加课外班的情况相同，所以学生数为7×(5-1)+1=29名。本题选B。
如果我们再遇到类似的问题，就可以按照刚才的思路去尝试解决问题啦。以上就是抽屉原理的解题方法，大家学会了吗？
短时间内找出不定方程的解
不定方程题目和普通方程最主要的区别就是题目是没有唯一解的，因此大部分考生解题会选择的方法就是代入排除法，但这样验证的弊端是考生解题时间会被答案的设置支配。想要掌握解题主动权，需要牢牢记住以下几点方法：
奇偶特性
例1：办公室工作人员使用红、蓝两种颜色的文件袋装29份相同的文件。每个红色文件袋可以装7份文件，每个蓝色文件袋可以装4份文件。要使每个文件袋都恰好装满，需要红色、蓝色文件袋的数量分别为( )个。
A.1、6 B.2、4 C.4、1 D.3、2
【答案】D【解析】两种文件袋合计29份文件，设有X个红色文件袋，Y个蓝色文件袋，得到：7X+4Y=29。由于29是奇数，在加减法算式中只有当7X与4Y这两个数一奇一偶时才会出现和为奇数的情况，由于4Y只能为偶数，因此推测出7X的结果一定是奇数，因此答案限制在A、D两个选项中，带入A选项，蓝色文件袋个数不是正整数。因此只能选择D选项。
方法总结：当遇到不定方程，结果与其中一项的奇偶性均已知时，可以根据奇偶特性排除答案。
整除特性
例2：张师傅每小时可以做50个面包或70个蛋挞，且每小时只能做面包或蛋挞中的一种。若张师傅做的面包和蛋挞共400个，则他用了( )个小时。
A.7小时 B.6小时 C.4小时 D.3小时
【答案】B【解析】设张师傅做了X小时的面包，Y小时的蛋挞，列出等量关系式：50X+70Y=400，化简得5X+7Y=40，观察结果与X的系数存在公约数5，据此可以推出7Y也一定是5的倍数，由于本题中Y最大只能取到5，因此Y=5，带入原式，即可解出X=1。所以共用时5+1=6小时。
方法总结：当不定方程的结果与其中一项存在公约数时，另一项也存在该公约数。
同余特性
例3：已知17X+10Y=149，X、Y均为正整数，则X的值是( )。
A.5 B.6 C.7 D.8
【答案】C【解析】将10Y与149同时除以10，10Y整除余数为0，149除以10后余数为9，根据余数的和等于和的余数，因此17X除以10后余数一定为9，结合选项，本题选择C选项。
方法总结：同余特性指的是：余数的和决定和的余数，余数的积决定积的余数，余数的幂决定幂的余数。但在实际应用中，大家也可以简单理解为：和是两个数相加得到，那么和的个位数也就是由两个加数的个位数相加得到，10Y的个位数一定为0，因此149的个位数9就一定来源于17X。
学会了这三种方法，遇到不定方程时，大家选择合适的方法，短时间内就可以选出正确答案啦！
行测数量关系“最不利原则”你了解吗？
在行测试卷中，数量关系部分题目难度相对较高，是很多考生备考的难点，提到总是会犯怵，但其中也会有一些题型，在掌握一定技巧后，可以相对轻松的解决，今天带领大家一起来学习一类题型——利用“最不利原则”求解极值问题。
题型特征
题目中出现“至少…才能保证…”。
解题原则
利用最不利原则解决题目时就是要考虑最不利情况，即与成功只有一步之差的情况，结果数=最不利情况数+1。
那到底如何利用最不利原则解决极值问题呢？我们来看几道题目。
经典例题
例1：在一个暗箱中，有4个黄球3个白球，至少从中取出几个球才能保证3个球的颜色相同？（ ）
A.1 B.3 C.5 D.7
【答案】C【解析】最不利情况是每种颜色的小球都恰好只取出了2个，最不利情况数为4，此时再取出1个，无论是黄球还是白球，都能保证取出3个颜色相同的小球，因此至少要取4+1=5个球。
有些最不利原则题目还会结合排列组合问题进行考查。我们一起来看一道例题。
例2：有四种颜色的文件夹若干，每人可取1~2个，至少有几人去取，才能保证有3人所取到的文件夹完全相同？（ ）
A.20 B.21 C.28 D.29
【答案】D【解析】由题可知，有四种颜色的文件夹若干，如果取1个文件夹，有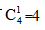
种情况，如果取2个文件夹，当两个文件夹颜色相同时，有
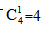种情况，当两个文件夹颜色不同时，有
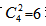种情况，共有4+4+6=14种情况。如果想保证3人取得文件夹完全相同，最不利情况是这14种情况每种都有2个人选择，那么此时再来1个人，无论选择哪种情况，都能保证有3人取得的文件夹情况完全相同，因此至少要有14×2+1=29个人，本题选择D项。
通过上述题目我们发现，利用最不利原则求解的题目，题型特征相对还是比较明显的，大家在平时要多多练习，做到熟能生巧。即使有时也会结合排列组合来考查大家，但实质上万变不离其宗，大家在备考期间要认真复习，做到真正掌握解题思路，对于这类问题而言难度也就不会太大了。最后祝大家能够获得令自己满意的结果，前程似锦！
坏钟和标准钟的同与不同
行测考试以时间紧、题量大著称，但是在大家认为比较难的数量关系部分，却存在着一些所谓“模型题”，出题方式相对来说比较固定，大家如果能够对这些题目有所认知，掌握解题方法，也是能够把它们变为简单题。这里带领大家一起来认识其中一种——坏钟问题。
坏钟问题形式
例题：一个时钟每小时慢4分钟，照这样计算，早上6：00对准标准时间后，当日晚上该时钟指向8：00时，标准时间是多少？（ ）
A.20：56 B.21：00 C.21：30 D.21：56
如上面这道题，坏钟问题的基本形式，就是有一个时钟走动的速度，与标准时间不一致，每小时或者每天，都会快一些或者慢一些，导致显示的时间不是标准时间，这就是坏钟与标准钟的不同，而由此引申出一系列问题，最常见的就是求标准时间是多少。当然，有时也会有一些变形。
解题原理和方式
坏钟虽然与标准时间不一致，但是一般走动速度也是均匀的，所以坏钟走过的时间与标准时间的比例是一致的，这是不同中隐藏的同。我们可以利用这个原理，根据题目已给的坏钟表示时间，求出实际时间，让坏钟也能报出准确时间。
例题：一个时钟每小时慢4分钟，照这样计算，早上6：00对准标准时间后，当日晚上该时钟指向8：00时，标准时间是多少？（ ）
A.20：56 B.21：00 C.21：30 D.21：56
【答案】B【解析】坏钟每小时慢4分钟，也就是说，标准时间过1小时，坏钟走过56分钟，不管过了多长时间，这个比例是不会变的，坏钟走过的时间：标准时间=56：60，现在早上6：00对准标准时间，此时坏钟与标准时间是一样的。当日晚上该时钟指向8：00时，坏钟过去的时间为14小时，则标准时间为14×（60/56）=15小时，即该时钟指向晚上8：00时，标准时间是21：00。故本题选B。
有时候，题目给出的比例，不一定是一个小时快几分钟或慢几分钟，而是以其他方式给出，但是其本质是不变的，依旧是坏钟走过的时间与实际时间的比值不变。
小结
如果题目最终给出的是坏钟时间，通过坏钟经过的时间与标准时间比值不变，可以求出标准时间。
如果题目最终给出的是标准时间，则可以分析标准时间过1小时与坏钟的差异，进而求出坏钟显示的时间。
行测数量关系中，类似的题目还有不少，大家在备考中除了学习基本的数学方法和思想，也要加强对这类比较固定题目的积累，双管齐下，共同提高。
三个方法帮你解答行测排列组合中的难题
在行测考试中，数量关系题目一直是考生们难以攻克的关卡，排列组合问题在数量关系中的难度更是首屈一指，但排列组合一直是近几年来的高频考点，属于必考题型。解决排列组合问题的常用方法有优限法、捆绑法、插空法，为了能够让大家对这三种方法有更深一步的了解，下面带领大家一起来学习排列组合中的三种解题方法。
优限法
当某元素或者位置有特殊要求限定时，应优先满足其要求，然后再对其它元素或位置进行排列。
例1：某宾馆有6个空房间，3间在一楼，3间在二楼。现有4名客人要入住，每人都住单间，要求一楼的房间必须住满。问宾馆共有多少种安排方法？（ ）
A.24 B.36 C.48 D.72
【答案】D【解析】因要求一楼必须住满，故可优先从4名客人中选择3人进住一楼单间，有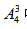
种选法，余下1名选择楼上3间中的1间，有3种选法，因此共有
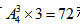种安排方法。
捆绑法
当有元素要求相邻时，可先将要求相邻的元素进行捆绑视作一个整体，再与其它进行排序，最后再考虑要求相邻的元素内部是否也需排序。
例2：6名同事一起去看演出，预定了同一排相邻的6个座位，其中要求甲、乙二人必须相邻而坐，则6人选择座位的情况一共有多少种？（ ）
A.120 B.240 C.480 D.720
【答案】B【解析】因甲、乙二人要求相邻，可先将二人捆绑，捆绑后与其他4人排序，有A5/5=120种方法；再考虑捆绑的二人内部的次序，有A2/2=2种方法。故所求为2×120=240种。
插空法
当有元素要求不相邻时，可先将其余元素进行排列；再将要求不相邻的元素插入到已排列元素形成的空隙中。
例3：一次小型文艺演出活动上有2个舞蹈节目，2个小品，2个唱歌节目。在制定节目顺序时，要求2个唱歌节目不能相邻演出，则共有多少种不同的演出顺序？（ ）
A.120 B.240 C.480 D.720
【答案】C【解析】因要求2个唱歌节目不能相邻，可先安排其余4个节目，有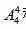
种排法；最后将2个唱歌节目插在其余4个节目所形成的5个空隙中，有
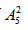种方法；故共有
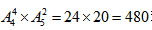种不同的演出顺序。
通过上面三道题目的讲解，相信大家对这三种方法有了更深一步的理解；元素有要求就先满足其要求，要求相邻则先捆绑，要求不相邻则用插空。希望大家在今后的学习中能熟练掌握这三种方法，也相信大家对排列组合的学习会更进一步。
