政华教育

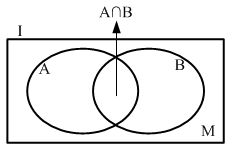
【答案】B【解析】我们可以利用文氏图来对题干信息进行简单的梳理。如用全集I表示班级总人数，集合A表示语文及格的人数，集合B表示数学及格的人数，则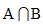表示两科都及格的人数，补集M表示两科都不及格的人数，这样，若想用各个部分拼凑出全集I，根据每一个区域不重复、不遗漏的原则，应用A+B，减去重复的部分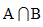，再加上遗漏的部分M，即：解得M=10人，选B。

例2

某单位共有240名员工，其中订阅A期刊的有125人，订阅B期刊的有126人，订阅C期刊的有135人，订阅A、B期刊的有57人，订阅A、C期刊的有73人，订阅B、C期刊的有64人，订阅3种期刊的有31人。问：没有订阅这三种期刊中任何一种的有多少人？（）

A.13 B.15 C.17 D.19

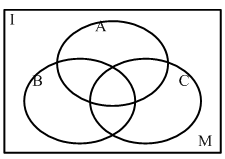
【答案】C【解析】我们同样可以利用文氏图对题干信息进行简单梳理。如用集合I表示员工总人数，集合A、B、C分别表示订阅A、B、C期刊的人数，则根据例题1，我们可以类比得出三者容斥的解题公式，即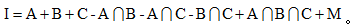：将本题数据代入公式，得到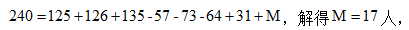选C。

例3

一批游客中每人都去了A、B两个景点中至少一个。只去了A的游客和没去A的游客数量相当，且两者之和是两个景点都去了的人数的3倍。则只去一个景点的人数占游客总人数的比重为( )。

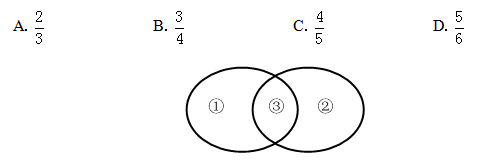
【答案】B【解析】利用文氏图梳理题干信息，则区域表示只去了景点A的游客人数，区域表示没去A的游客人数，区域表示两个景点都去了的游客人数。由题意，可设区域①、②的人数为x人，则有2X=3X,即区域的人数为(2/3)X人，则所求为X+X/X+X+(2/3)X=3/4,选B。

以上就是为大家介绍的容斥问题的基本内容，相信大家结合相应的题目练习之后，一定会对容斥问题有新的认识。

浓度问题其实很简单

说起浓度问题，很多人就开始皱起眉头，一种“题不醉人人自醉”的感觉，可是浓度问题真的有那么可怕吗？其实并不，在解决浓度问题的时候，只要把握几个关键点，很多题目都可以迎刃而解。那什么是浓度问题呢，其实不止是在数量关系题目中，生活中也经常会碰到浓度问题，回想下自己买奶茶的时候，是不是经常被问到，是要少糖，中糖，还是多糖？其实奶茶小哥就是在问你浓度的问题，你是要糖的浓度低一点还是高一点呢？没想到吧！所以浓度问题无所不在，而浓度问题也很简单，浓度的基本公式为浓度=（溶质/溶液）×100%，如一杯糖水的浓度指的就是溶质(糖)的量/溶液(糖水)的量，也就是浓度越高，也就越甜。

那接下来我们就来研究一下，浓度问题在数量关系当中如何快速求解吧！

例1

有两瓶质量均为1千克的酒精溶液，浓度分别为70%和45%，先从两瓶中各取部分混合成1千克的酒精溶液，测得浓度恰好为50%，再将这两瓶中剩下的溶液混合，则所得酒精浓度是：（）

A.50% B.55% C.60% D.65%

【答案】D【解析】两瓶溶液的溶质质量分别为1×70%=0.7千克、1×45%=0.45千克，第一次取出混合后的1千克溶液中含有溶质1×50%=0.5千克，则余下溶液混合后含有溶质0.7+0.45-0.5=0.65千克，而溶液剩余1千克，即浓度为0.65÷1×100%=65%。选择D选项。

总结：不管溶液怎么混合，浓度基本公式要记牢，让最终求浓度，就找所需溶质和溶液的量，若能直接表示出所需溶质和溶液的量，即可直接求解。

例2

在一杯清水中放入10克盐，然后再加入浓度为5%的盐水200克，这时配成了浓度为2.5%的盐水，问原来杯中有清水多少克？（）

A.460克 B.490克 C.570克 D.590克

【答案】D【解析】设原来杯中有清水x克，则根据混合前后溶质总量不变，可得，10+200×5%=（X+10+200）×2.5%，解得x=590。选择D选项。

总结：如果不能直接求解所求量，把握一点，即不管有多少溶液混合在一起，就结合混合前后溶质和溶液总量不变，列方程，大多即可迎刃而解。

总结：溶液混合问题除了根据溶质，溶液总量不变列方程，也可根据十字交叉求解，两部分浓度写左边，整体浓度写中间，沿着十字线作差，差值的比值即为两部分对应溶液量的比值。

通过以上题目分享，希望大家不再为浓度问题发愁，从此“奶茶”甜度随便选。