政华教育

【答案】B【解析】通过题目描述可知题目中出现两种销售方式：“量贩式超市”“便民小超市”，不妨在表格中将这两种方式表示出来，进而表示出两种方式的售价分别是12元和13.5元以及各自的销量600件和400件，并且给出总利润为5000元，需注意：总利润=总售价-总成本，但是题中没有给出成本，所以，不妨设单件成本为x；则有：

12×600+13.5×400-(600+400)×x=5000，解得x=7.6。

故答案选择B项。

例2

服装店买进一批童装，按每套获利50%定价卖出这批童装的80%后，按定价的八折将剩下的童装全部卖出，总利润比预期减少了390元。问服装店买进这批童装花了多少元？（）

A.5500 B.6000 C.6500 D.7000

【答案】C【解析】通过题目可知这批童装在销售时分为打折前和打折后两个阶段，所以不妨在表格中将这两个阶段表示出来，接着题目说“按每套获利50%定价卖出这批童装的80%”，此时给出打折前的利润率为50%，需注意：利润率=售价/成本-1；此时如果设成本为y，则刚开始的定价应为1.5x；同时已知打折前卖出80%，其实也就是总销量的80%，但总销量未知，所以如果设总销量为x，则打折前售出0.8y，之后“定价的八折将剩下的童装全部卖出”，即打折后的售价应为：1.5x×0.8=1.2x，同时打折后的销量为1-0.8y=0.2y，最后题目给出等量关系“总利润比预期减少了390元”，其实就是：按原定价销售完的总利润-(打折前的总利润+打折后的利润)=390元。之前已表示出两个阶段的成本、售价、销量；所以两个阶段分别的总利润=单套利润×销量；而单套利润=售价-成本，把出现的基本概念全部表示在表格中，再根据等量关系就有：

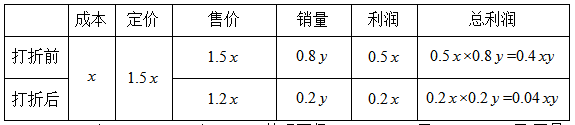
0.5xy-(0.4xy+0.04xy)=390，整理可得0.06xy=390元，xy=6500元，而最终题目求：“服装店买进这批童装花了多少元？”即求这批服装的总成本，总成本=单件成本×总销量=xy=6500元，故答案选择C项。

通过以上两道题可以看出来，不管题干中的销售方式有多复杂，只要在读题的过程中能够结合表格法把其中的成本、定价、售价、销量、利润等梳理清楚，问题就可以迎刃而解。表格一出，问题解决，各位考生，动起来吧！

数量关系之货物集中“取点看”

在行测考试当中，数量关系往往是比较难的一部分内容，尤其是统筹问题，它需要我们利用数学来研究人力、物力的运用和筹划，使它们能发挥最大效率。此类问题对思维的要求比较高，往往研究的内容看似复杂但是技巧性很强。今天带大家来学习统筹问题常考的一种类型——货物集中。

货物集中问题：是一类集中统筹问题，是指将货物集中的同时，求解如何集中能够使得运费最少。

解题原则：确定一点，判断该点两端货物的重量，把轻的一端向重的一端集中。在操作过程中我们无需考虑各位置之间的距离，只需考虑货物的重量即可。接下来，我们通过一道例题来详细说明此类题目如何快速求解。

例题

一条直线上依次有甲乙丙丁四个煤场，相邻两个煤场之间的距离都是3千米，目前甲有煤100吨，乙有煤90吨，丙有煤12吨，丁没有煤。现在要将四个煤场的煤集中到一个煤场，已知1吨运输1千米的花费是10元，那么为使得运费最少，则应该把煤集中到哪个煤场？（）

A.甲 B.乙 C.丙 D.丁

【答案】B【解析】运输单价不变，相邻两个煤场之间的距离固定，将轻的一端向重的一端更划算，无需考虑距离。在甲和乙之间确定一点，则左边货物共100吨，右边的货物共102吨，因此往右边集中即乙、丙或丁，排除A选项。再从乙丙之间确定一点，左边总重190，右边总重12，根据解题原则应向左集中，故乙为最合适的集中位置，故选B。

掌握了货物集中问题的解题原则，我们来通过两道练习题练习巩固一下。

练习1

在一条公路上每隔10里有1个集散地，共有5个集散地。其中1号集散地有旅客10人，3号集散地有旅客25人，5号集散地有45人，其余两个集散地没有人。如果要把所有人集中到一个集散地，那么所有旅客所走的总里数最少是多少？（）

A.1100 B.900 C.800 D.700

【答案】B【解析】读完题后我们发现这道题的本质也是货物集中问题，因此先根据货物集中的解题原则先去确定最优的集散地然后再去计算。首先把点取在1号和2号之间，左边有10人，右边有70人，往多的一端即右边集中，而2号没有人，所以将点设在2号、3号之间与1号、2号之间相同。再把点取在3号和4号之间，左边有35人，右边有45人，往多的一端即右边集中。而4号集散地没有人，同理将点继续往右边集中，移动到了5号集散地。故该地为最优集散地。计算总里数为：10×40+25×20=900。

故答案选B。

练习2

某个公司在甲、乙、丙三个地方各有一个仓库，三个地方在一条直线上，之间距离分别相距6km，10km，甲仓库有5吨货，乙仓库有8吨货，丙仓库有12吨货，如果把所有的货物集中到一个仓库，每吨货物每千米运费是100元，请问把货物放在哪个仓库最省钱？运费最少为多少？（）

A.甲、12000 B.乙、13000 C.丙、14000 D.乙、15000

【答案】D【解析】在甲乙之间确定一点，左边总重5吨，右边总重20吨，最省钱地应为乙或丙，排除A。接着在乙丙之间取一点，左边总重13吨，右边总重为12吨，根据解题原则，应该向左移动，所以确定将位置定在乙仓库最省钱。其运费为5×100×6+12×100×10=15000。故本题选D。

通过以上例题的精讲和展示，会发现只要掌握好了货物集中的问题的解题思路，这样大家会发现不仅可以很大程度地缩减我们每个距离、价格的计算的过程，也能提高正确率和准确率，那么希望以后考生们多多地加强这类型题目的方法的思维，做到举一反三，则以后遇到这类问题就可以迎刃而解。

三种特值告诉你工程问题可以很简单

工程问题在行测数量关系的题目中经常出现，并且相对来说是比较简单的，只要我们掌握了一定方法会发现这一类题目其实还是值得一做的。因此通过几个例题来告诉大家，工程问题到底怎么来解决。

例1

一项工程，甲单独做要10天，乙单独做要15天。若甲、乙两人合作，需要多少天？（）

A.5 B.6 C.7 D.8

【答案】B【解析】这道题中，我们会发现题目中出现了甲完成此项工程的时间，也出现的乙完成此项工程的时间，那我们想要求出合作的时间就需要知道此项工程的工作量和甲、乙的工作效率，所以这里不妨我们设总工作量为“1”。则甲的工作效率为1/10，乙的效率为1/15，因此合作效率为1/10+1/15=1/6，因此需要1÷（1/6）=6天。所以这道题选B。

这道题在计算时其实是有分数计算的，有没有什么方法可以再简单一点呢？其实无论设工作总量为多少都不会影响最终的结果，为了计算简便，就要让效率为整数。如果效率为整数就要让工作总量为时间的倍数，所以也可以设时间的最小公倍数为工作总量。设工程总量为10、15的最小公倍数30，则甲的工作效率为3，乙的工作效率为2，则甲、乙两人的合作效率为3+2=5，故甲、乙两人合作需要30/5=6天。故本题选B。

总结：题目中出现完成同一项工程的多个时间时，可以设时间的最小公倍数为工作总量。

例2

甲、乙两队完成一项工程的效率比为2∶5。该项工程，若由甲队先单独做3天，再由乙队单独做4天，最后由甲、乙两队合作6天刚好完成。问若由甲队单独完成，需要多少天？（）

A.32 B.33 C.34 D.35

【答案】C【解析】这道题中想要求出甲单独完成要多久就需要知道整个工程的工作量，还有甲的工作效率。题目中出现了甲乙的效率之比，不妨结合比例设他们的效率分别为2x、5x，那整个工程的工作量就为3×2x+4×5x+6×（2x+5x）=68x。故甲队单独完成需要68x/2x=34天。而这里我们发现其实到最后我们所设的x约掉了，所以直接设工作效率之比为工作效率就好了，因此不妨设甲、乙两队的工作效率分别为2、5，则工作总量为3×2+4×5+6×（2+5）=68，故甲队单独完成需要68/2=34天。故本题选C。

总结：题目中出现了工作效率之比，按最简比设工作效率。

经过上面几个题目的解析，大家可以发现，只要掌握了方法，工程问题也可以很简单。