政华教育

在行测考试中，数量关系部分的利润问题是近几年考查频率较高也是比较贴近生活实际的，但是部分题目由于涉及概念较多，在梳理题干信息时常常没有头绪。那我们怎么能够把题干信息梳理的清晰明了呢？其实我们的方法很简单，对于题目条件比较多且概念比较复杂的题目，我们不妨用表格把它们整理好再来找等量关系计算。下面通过题目带大家来看看。

例1

甲用1000万元购买了一件艺术品并卖出，获利为买进价格的10%，随后甲用艺术品卖出价格的90%买入一件珠宝，并以珠宝买进价格的九折卖出。若上述交易中的其他费用忽略不计，甲最终：（）

A.盈亏平衡 B.盈利1万元

C.盈利9万元 D.亏损1.1万元

【答案】B【解析】梳理题干的条件列表如下(根据题干描述顺序依次求值列表)：

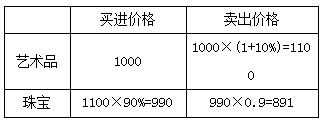
故甲最终盈利(1100-1000)+(891-990)=100+(-99)=1万元，本题选B。

在上述题目当中我们发现涉及到艺术品和珠宝两件物品的买进和卖出，为了更好的表达两者的价格变动，我们列了两列表格来梳理。当然有的时候还是会涉及到销量或者多次出售等复杂的情况，我们也能通过表格把利润问题精细化。下面再来看两道题目：

例2

某企业生产一种产品，每件成本价是400元，销售价为510元。为进一步扩大市场，该企业决定在降低销售价的同时降低生产成本，经过市场调研，预测下季度这种产品每件销售价降低4%，销售量将提高10%。要使销售利润保持不变，该产品每件的成本价应降低多少元？（）

A.7.6 B.10.4 C.13.2 D.16

【答案】B【解析】设下季度每件成本价为x元，本季度销售y件，梳理题干可列表如下：

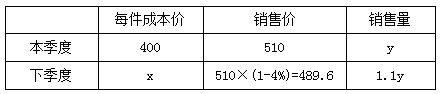
根据销售利润保持不变这一等量关系可得：(510-400)×y=(489.6-x)×1.1y，解得x=389.6，则成本价降低400-389.6=10.4元，故本题选B。

上述两道题目均涉及到条件比较多、概念比较复杂的利润问题的概念，单独依靠在题干上标记的方法，难以理清题干信息，而通过列表的方式可以将概念间关系更加直观、清晰地表示出来，再通过题干描述等量关系或表格内概念存在的计算关系，最终列方程计算出答案。

如何解决牛吃草，追及思维要用好

很多同学认为数量关系是行测考试中很难的一部分，所以会直接放弃，但这是一种比较错误的认识，实际数量关系有许多基础的题型是比较简单的，并且在近几年的国省考中，对于知识点的考查还是比较灵活的，所以平时还是要多积累基础的题型。今天就给大家介绍数量关系里的一个基础题型——牛吃草问题。

一、牛吃草问题的特征

一般牛吃草问题的题目中会出现包含数量和时间信息的排比句，例如：“草地上原有一片牧草，草每天是匀速生长的。放养20头牛，30天可以吃完；放养25头牛，20天可以吃完；若放养30头牛，几天可以吃完”。题目中出现了3句话都包含牛的数量和时间信息，那么这类问题就可以定义为牛吃草问题了。

二、用好追及思维，解决牛吃草问题

例1

牧场上有一片青草，每天牧草都匀速生长。这片牧草可供10头牛吃20天，或者15头牛吃10天。问：可供25头牛吃几天？（）

A.3 B.4 C.5 D.6

【答案】C【解析】题目中出现了牛的数量和吃草时间相关的排比句，可以认为是牛吃草的问题。根据题目信息可以知道，①牧场上原有一定量的牧草，②牧草每天生长，③牛每天都在吃草；牛吃这片牧草的过程，我们可以看作是牛在后边吃，草在前边均匀生长的追及过程，当草被吃完时便相当于“牛追上了草”。根据追及问题公式路程差=速度差×时间，路程差即为原有的草量，由于是“牛追草”，速度差即为牛每天吃草的速度-草每天草生长的速度，可以得到：原有草量=(牛每天吃掉的草-每天生长的草)×时间；可以假设每头牛每天吃的草量为“1”，每天生长的草量为X，可供25头牛吃T天，所以原有草量=(10-X)×20=(15-X)×10=(25-X)×T；解方程得X=5；t=5，故本题选择C项。

通过上述的题目，我们可以用追及思维去解决牛吃草问题；但有些题目中并不是牛去吃草这种表述，但是只要符合“牛吃草”问题的特征，那我们也同样可以用牛吃草的解题思维来求解，例如下面的这道题目：

例2

某招聘会上在入场前有人就开始排队，并且每分钟来的人一样多。从开始入场到等候入场的队伍消失，若开4个入场口需要30分钟，开5个入场口需要20分钟，如果同时开6个入场口，需要多少分钟？（）

A.8 B.10 C.12 D.15

【答案】D【解析】题目中出现了入场口数量和时间相关的排比句，从外形上看可以认为是牛吃草问题。根据题目信息可以知道，入场口每分钟都在有人入场，相当于“牛在吃草”，而每分钟也会有人来排队，相当于“草在均匀生长”，入场前的人数相当于“原有的草量”。设每个入场口每分钟入场人数为1，每分钟的排队人数为X，所求为T，根据入场前的人数=(入场口数量-每分钟来的人数)×时间；所以(4-X)×30=(5-X)×20=(6-X)×T；解方程得X=2，T=15；故本题选择D项。

这就是用追及的思维解决牛吃草的问题，大家学会了吗？建议大家在备考期间多多练习，熟练掌握这类问题，希望对大家的备考有所帮助。

行测数量关系中用定位法求概率

无论是在国家公务员考试中还是省考里，数量关系都是不可分割的一部分，虽然题目量不是特别多，但是想在短时间里全做对还是有一定难度的。因此我们就需要利用一些方法去解题，从而节约自己做题时间。而在数量关系里都会有一个章节“古典概率”，求古典概率很多同学第一时间会想到用公式求解，今天给大家介绍一种快速求解方法——定位法，下面我们一起学习下：

一、定位法使用条件：

①古典概率求解概率

②遇到要同时考虑相互联系的元素时

③无论第一个选哪个位置，不影响后面选择的可能性。

二、定位法具体步骤：

先固定其中的一个元素，再考虑另外一个元素的可能状态，接下来我们通过几个例题去感受下。

经典例题

【例题1】一张纸上画了5排共30个格子，每排格子数相同，小王将1个红色和1个绿色棋子随机放入任意一个格子(2个棋子不在同一格子)，则2个棋子在同一排的概率：（）

A.不高于15% B.高于15%但低于20%

C.正好为20% D.高于20%

【答案】B【解析】答案选择B选项。解析：方法一，将2个不同颜色的棋子随机放入30个格子中，样本总数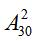。5排共有30个格子，每排有6个格子，则2个不同颜色的棋子在同一排，样本数为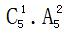

。故经计算2个棋子在同一排的概率为。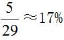

方法二，5排共有30个格子，则每排有6个格子。先从30个格子中任选1个安排红色棋子，此时还剩下29个空格子。若想2个棋子在同一排，则绿色棋子只能挑选红色棋子所在排剩余5个格子中的一个，则2个棋子在同一排的概率为。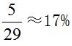

【例题2】某单位工会组织桥牌比赛，共有8人报名，随机组成4队，每队2人。那么小王和小李恰好被分在同一队的概率为( )：

【答案】A【解析】假设小王已经分好队，剩下7个位置小李可以选择，即总的样本数为7，要想和小王一队，只有一种情况，即所求事件的样本数为1，故两人被分在同一队的概率是。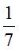

通过上面两个题目对比大家可以发现在做古典概率题目的时候有时候公式求解会稍微复杂一点，这个时候如果我们能判断出来符合定位法的使用条件，就可以利用定位法快速解题。所以希望各位同学能够多加练习，争取在做题的时候能够学会利用定位法解题。

“一副扑克牌”玩转行测最不利原则问题

行测数量关系考察内容广泛，题型灵活多样，让很多考生在备考时束手无策。实际上，只要把握住每种题型的特征和解题原则，以不变应万变，数量关系问题就可迎难而解。比如，我们有时会遇到这样一类问题，题干中会出现“至少.....才能保证...”这样的字眼，这类问题我们称之为最不利原则问题。今天带着大家了解最不利问题其中的奥秘。

1.何为“最不利”

最不利，就是最倒霉，最坏的情况。举个例子：假设手里有一把锁，10把钥匙，其中只有一把钥匙能打开这把锁。最幸运的情况，我们试一次就可以打开锁。而最坏的情况呢？需要把所有钥匙都试过，即10次，才能把锁打开。

2.题型特征

题干中出现“至少......才能保证...”

3.解题原则

最不利情况数+1

例题精讲

一副完整的扑克牌共计54张(包含大小王)，其中A、J、Q、K分别对应点数1、11、12、13。

【例题1】至少抽出( )张才能保证一定有2张牌花色相同？

【答案】7【解析】一副扑克牌有4种花色，黑桃、红桃、梅花、方块。外加，大小王各一张。如果想保证有两张牌花色相同，考虑最不利的情况，首先取出不满足题意的大小王两张，接下来，如果我们再取一张，可能是黑桃。下一张，一定能保证是黑桃吗？不能，可能是红桃。接着取，下一张，一定能保证是黑桃或者红桃吗？不能，可能是梅花。下一张一定能保证是黑桃，红桃，或者梅花吗？不能，可能是方块。而此时我们再抽一张牌，无论是哪一种花色，必然存在有种花色是2张牌。

因此，要保证有2张花色相同，考虑最不利情况，需要先取出特殊元素(大小王2张)，然后，四种花色每一种都取1张牌，最后再抽一张即可，即抽2+4+1=7(张)。

【例题2】至少抽出( )张才能保证一定有3张牌点数相同？

【答案】29【解析】一副扑克牌有1-13共13种点数，外加，大小王各一张。考虑最不利的情况，即先取出不满足题意的大小王两张，再将每种点数(共13种)各取2张，此时再抽一张牌，这一张一定是13种点数中的某一种，就构成了3张牌点数相同，即抽2+2×13+1=29(张)。

综上可知，解决最不利原则问题，重点需要找到最不利的情况，而最不利情况就是最倒霉的，最坏的情况。希望各位考生把握住这一点，快速破题，加油！