政华教育

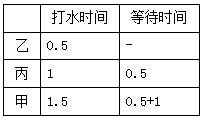
【答案】B【解析】每人花费的时间包括两部分：打水时间和等待时间。第一个人打水时，其他两人等待，第二个人打水时，剩下一人等待，最后一个人打水时，没人等待。每人打水时间是固定的，因此想要时间总和最少，就要让等待时间尽可能短，等待的人越多时，打水时间越短越好，这样总的等待时间越短，所以应该让用时短的先打，长的后打。最合理的顺序为：乙、丙、甲。那么每人花费的时间如下表所示，故花费的时间总和最少是0.5×3+1×2+1.5×1=5。

二、有多个水龙头时，如何排队更省时

【例题2】公用电话亭中有两部电话，六个人排队打电话，打完即走，他们的通话时间分别为3分钟、5分钟、4分钟、13分钟、7分钟、8分钟，则大家在此公用电话亭逗留的总时间最少为( )分钟。

A.60 B.66 C.72 D.78

【答案】B【解析】两部电话可以同时进行，通话时间固定，想让逗留的总时间最少，就要让等待时间尽可能少，那就让通话时间短的人先打电话，六个人按时间从短到长排序：3分钟、4分钟、5分钟、7分钟、8分钟、13分钟，先让用时最短的两个人分别去两部电话(1号和2号)，每部电话用完后让剩下的人中时间最短的接着用，先把六人分成两组，分配情况如下表：

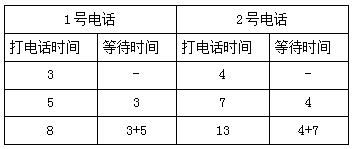
所求总时间为3×3+5×2+8+4×3+7×2+13=66。故本题选B。

通过上述方法，我们可以发现，排队取水问题并没有那么复杂，只需要让打水时间短的人先打，排好打水顺序后确定每个打水时间对应的人数，最后计算出总时间就可以了。

拒绝无效读题，表格帮你梳理题干

【例题1】甲、乙、丙三人各出100万元资金购买某种每股10元的股票，当股价涨到12元时甲卖出50%，丙卖出20%；当股价涨到15元时甲卖出剩余部分的20%，乙卖出60%；此后股价回落到13元时三人全部卖出剩余股票。如不计税费，则此次投资获利最高的人比获利最低的人多赚多少万元？（）

A.1 B.14 C.15 D.18

【答案】C【解析】已知甲、乙、丙三人各出100万购买每股10元的股票，即起始时三人均持有10万股。由于本题略长且涉及到的人和股价较多，仅仅通过通读题目，没办法把题意了解透彻，而问题问的又是获利最高的人比获利最低的人多赚多少钱，想要求解这一问题，就必须把三人在三个股价阶段的获利情况梳理清楚。那接下来我们就通过列表的方式梳理一下甲、乙、丙获利情况，可得下表：

所以，甲共获利10+5+12=27、乙共获利30+12=42、丙共获利4+24=28，所以获利最高的人乙比获利最低的人甲多赚42-27=15万元。故本题选C。

在上述题目中，我们发现通过表格可以清晰地分析出每个人的获利情况，更高效地解答获利最高的人比获利最低的人多赚多少万元。

【例题2】某种商品第一天原价销售，第二天开始每天的价格比上一天下降原价的10%。在最后一天之前，每天的销量比上一天提高100%，最后一天的销量与第三天相同，总共6天全部卖完。如果这种商品的成本为原价的60%，则销售这种商品的总利润为总成本的：（）

A.不到10% B.10%~20% C.20%~30% D.30%以上

【答案】B【解析】假设这种商品的原价为x，第一天的销量为y。根据题意，商品每天的售价下降x×10%=0.1x，每天的销量为上一天的2倍(其中最后一天的销量与第三天相同)，且每件商品的成本为x×60%=0.6x。那么这种商品6天的售价、销量以及每天的利润如下表所示：

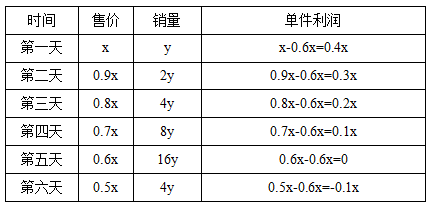
综上，商品的总利润为这六天利润之和0.4xy+0.6xy+0.8xy+0.8xy+0+(-0.4xy)=2.2xy，而总成本由于单件成本不变，所以总成本=单件成本×总销量=0.6x×(y+2y+4y+8y+16y+4y)=21xy。则销售这种商品的总利润为总成本的2.2xy÷21xy≈10.5%，在10%和20%之间。故本题选B。

对于本题，想要求总利润与总成本之间的关系，就得理清楚这六天的利润和成本的情况，由于涉及的天数较多，为避免混乱，表格法整理必是首选。另外，需要注意的是，审题要仔细，售价是每天都下降原价的10%，而销量是比上一天多1倍。

不知道通过这两个题目的分析，大家有没有感受到表格的魅力？磨刀不误砍柴工，看起来我们好像是多花费了列表的时间，但其实是用这部分时间更好地理解了题意。所以当题干略长，涉及的数据较多，理清题意有困难时，大家要学会善用表格这个“好帮手”。

如何搞定“不定方程”

【定义】

不定方程指的是方程或方程组中未知数的个数多于独立方程的个数。

例如：3x+4y=25

对于这个方程，它的解实际上是和未知数的取值范围有关的，而在考试中x、y通常都是正整数，那我们该如何求出x、y的值呢？通常情况下，如果所求的未知数就在选项中，则可以将选项代入，满足方程即为正确答案，但是四个选项挨个代入又比较耗费时间，那我们看下在正整数范围内能否通过数字特性先缩小未知数的取值范围，之后再将选项代入来达到快速求解的目的。

【求解方法】

1.整除特性：当未知数前面的系数与常数项存在公约数时，考虑用整除特性。

【例题1】小张的孩子出生的月份乘以29，出生的日期乘以24，所得的两个乘积加起来刚好等于900。问孩子出生在哪一季度？（）

A.第一季度 B.第二季度 C.第三季度 D.第四季度

【答案】D【解析】根据题意，设出生月份为x，出生日期为y，可得29x+24y=900。由于x、y为月份和日期，因此均为整数，观察可知24与900都能被12整除，则29x也能被12整除，即x必能被12整除。因x表示月份，故只能为12月份，即第四季度，故本题选择D。

2.奇偶性：当未知数前面的系数奇偶性不同时，考虑用奇偶性。

【例题2】办公室工作人员使用红、蓝两种颜色的文件袋装29份相同的文件。每个红色文件袋可以装7份文件，每个蓝色文件袋可以装4份文件。要使每个文件袋都恰好装满，需要红色、蓝色文件袋的数量分别为多少个？（）

A.1，6 B.2，4 C.3，2 D.4，1

【答案】C【解析】根据恰好“装满”，设红、蓝文件袋数量分别为x、y个，可得7x+4y=29。由于x、y为文件袋个数，因此均为整数。4y是偶数，29是奇数，因为奇数+偶数=奇数，则7x必是奇数，即x为奇数，排除B、D，代入A选项等式不成立，故本题选C。

3.尾数法：当未知数前面的系数为5的倍数时，考虑用尾数法。

【例题3】有271位游客欲乘大、小两种客车旅游，已知大客车有37个座位，小客车有20个座位。为保证每位游客均有座位，且车上没有空座位，则需要大客车的辆数是多少？（）

A.1辆 B.2辆 C.3辆 D.4辆

【答案】C【解析】根据每位游客均有座位“且”车上没空座位，设大客车x辆、小客车y辆，可得37x+20y=271，由于x、y为客车辆数，因此均为整数。20y的尾数为0，271的尾数为1，则37x的尾数必为1，即x的尾数为3。只有C选项符合题意，故本题选C。

对于不定方程的题目，未知数在正整数范围内，我们可以首先考虑用数字特性来缩小未知数的取值范围，之后再将选项代入，这样不仅可以大大缩短做题时间，而且使用起来也更加方便。

通过以上题目也不难看出，不定方程的题目难度还是较低的，只要我们掌握了相应的解题技巧再加上不断的练习，再“不定”的方程我们也能搞定。

排列组合问题解答技巧

【问题描述】

排列组合问题是一类求“方法数”或“选法数”的计数问题。

【常用解题方法】

优限法：优先考虑有绝对限制的元素或位置。

捆绑法：解决元素相邻问题；把要求相邻的元素捆绑在一起，看成一个整体，既要考虑捆绑元素内部的顺序要求，也要考虑整体的顺序要求。

插空法：解决元素不相邻问题；优先考虑其他元素的顺序要求(无要求的元素)，再将要求不相邻的元素插空排入，还要考虑不相邻元素的顺序要求。

间接法：正难则反；题干描述出现“至少”“不少于”“至多”，考虑用全部情况数-相反情况的情况数。

【常见考法】

(一)优限法

【例题】用1、2、3、4、5组成一个无重复数字的五位数，组成数字是偶数有几种情况？（）

【答案】48【解析】偶数的特征末位数字可以被2整除。末位数字有要求，优先考虑，可以被2整除，那就在2、4中选一个，情况数为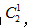剩下4个数顺序不同结果不同，4个数的顺序为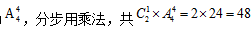种情况。

(二)捆绑法

【例题】用1、2、3、4、5组成一个无重复数字的五位数，组成数字是奇数相邻、偶数也相邻有几种情况？（）

【答案】24【解析】要求奇数相邻，偶数也相邻，那我们就把要求相邻的元素捆绑看成一个整体，即奇数1、3、5为整体，偶数2、4为整体。先考虑捆绑元素内部的顺序，1、3、5顺序不同结果不同，这三个数的排列情况为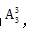2、4的排列情况为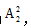两个整体的顺序不同结果不同，排列方式为分步用乘法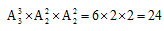种情况。

(三)插空法

【例题】用1、2、3、4、5组成一个无重复数字的五位数，组成数字是偶数不相邻有几种情况？

【答案】72【解析】要求偶数不相邻，我们就优先排其他无要求的元素，即优先考虑奇数，1、3、5顺序不同结果不同，1、3、5的排列方法共有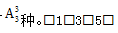形成四个空，只要任选两个排入偶数就能保证偶数2、4不相邻，2、4顺序不同结果不同，从4个空中选2个空且顺序对结果有影响用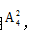分步用乘法，所以总的情况数为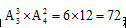种。

(四)间接法

【例题】共有3个白球，6个红球，从中任选3个球，白球不少于1个有几种情况？

【答案】64【解析】要求白球数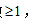白球数可以为1、2、3，情况数较多计算复杂，可以用间接法，用总的情况数-相反的情况数。白球数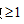的相反情况为白球数<1，即白球数为0。总的情况数为从9个球中选3个球记为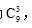白球数为0即3个球都是从红球里选记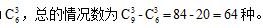

除了以上方法之外，比较常用且易于掌握的方法就是树状图，它能更好的帮助分析问题。

【例题】小王和小张各加工了10个零件，分别有1个和2个次品。若从两人加工的零件里各随机选取2个，则选出的4个零件中正好有1个次品的概率为：（）

A.小于25% B.25%～35% C.35%～45% D.45%以上

【答案】C【解析】A事件发生的概率公式：

总事件数：从两人加工的零件里各随机选取2个，选出4个零件

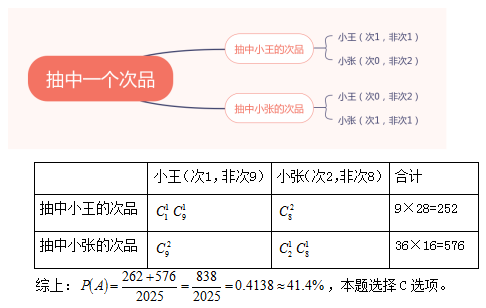
通过以上几种考法，我们发现，只要掌握排列组合的核心计算关系及解题技巧，结合题目中的要求，就可以列式求解，同时要注意题目中的细节。希望广大考生通过此种题型的学习，可以快速有效地解决排列组合为问题的考题，把这类题目的分数拿到手中。