
行测数量关系指导
排列组合问题“错位重排”
在行测考试当中,很多考生觉得排列组合问题比较复杂,但实际上在排列组合问题当中,有一类题目通过判断题型加上记忆结论就可以选出答案。
【例题1】编号为A、B、C的三个信封分别装有a、b、c三封信,现在要把三封信重新装入信封,且都不能和开始时的位置相同,问共有几种装法?( )
A.2 B.6 C.9 D.12
【答案】A【解析】题目中要把3封信的位置重新分装,且都不能在原来的信封中。由于元素较少,我们可以通过枚举法来解决。

可以看到本题共有2种装法。故本题选A。
上述题目当中相当于要把3个元素(信)的位置(信封)重新排列,使得每个元素都不在原来的位置上,这类题目我们称之为“错位重排”。当元素较少时我们可以通过枚举法将所有结果罗列出来。但是当元素过多时,情况比较复杂,再用枚举法显然不合适,所以需要我们熟记错位重排的常用数据以及递推公式。
【题型特征】
把几个元素的位置重新排列,使每个元素都不在它原来的位置上。
【递推公式】
将n个元素的错位重排数记为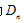 ,则:
,则:

【例题2】某集团企业5个分公司分别派出1人去集团总部参加培训,培训后再将5人分配到这5个分公司,每个分公司只分配1人。问5个参加培训的人中,有且仅有1人在培训后返回原分公司的情况有多少种?( )
A.42 B.43 C.44 D.45
【答案】D【解析】首先选出回到原来分公司的那个人,即5人中选1人,有5种情况;其次,剩下4人符合错位重排特征,共有9种情况;最后,两步情况数相乘得5×9=45种情况。故本题选D。
小小正反比,解题大能量
正反比的含义为:对于存在M=A×B关系的题目,若M不变,A和B成反比;若A不变,M和B成正比;若B不变,M和A成正比。只要题干存在M=A×B的关系,并且能找到其中的不变量,就可以利用正反比来解题,接下来带大家一起看两道例题,感受一下正反比的魅力。
【例题1】空军某部队运送救灾物资到灾区。原计划飞机每分钟飞行12千米,由于灾情严重,飞机速度提高到每分钟15千米,结果比原计划提前30分钟到达目的地。则机场到灾区的距离是( )千米?
A.1600 B.1800 C.2050 D.2250
【答案】B【解析】本题为行程问题,存在s=v×t,且由题可知两种飞行方式路程s不变,那么v和t成反比,原计划和实际速度比为12:15=4:5,则原计划和实际时间比为5:4,说明原计划用5份时间,实际用4份时间,差1份时间,对应题干的30分钟,那么原计划时间为5×30=150分钟,实际时间为4×30=120分钟。机场到灾区的距离为12×150=15×120=1800千米。故本题选B。
【例题2】某公司计划采购一批电脑,正好赶上促销期,电脑打9折出售,同样的预算可以比平时多买10台电脑。问该公司的预算在平时能买多少台电脑?( )
A.60 B.70 C.80 D.90
【答案】D【解析】本题没有太多的数据,第一眼看感觉好像不能做,但是仔细分析,存在关系:预算=单价×数量,根据题干可知预算不变,那么单价和数量成反比,原计划和打折后单价之比为10:9,数量之比为反比,即9:10,也就是原计划能买9份电脑,实际可买10份电脑,差1份电脑,对应题中的10台电脑,那么原来(平时)能买9×10=90台电脑。故本题选D。
以上就是两道数量关系中正反比题目的展示,大家可以看出来知识点不是很难,只要我们能找M=A×B的关系以及不变量,就能够利用正反比解决相关问题。
解决最不利问题需要“坏运气”
今天为大家介绍数量关系中一种常见题型:最不利原则。
【基础理论】
1.题型特征
【例题】一个不透明的袋子当中有4个黑球和4个白球,所有球除了颜色不同外,形状和大小都相同。
(1)请问至少要从袋子中拿出多少球可能有2个球的颜色不同?( )
A.2 B.3 C.4 D.5
(2)请问至少要从袋子中拿出多少球才能保证有2个球的颜色不同?( )
A.2 B.3 C.4 D.5
上面的例题当中,我们的目的都是使2个球颜色不同,但是这里需要区分这两种问法的不同之处:问题(1)的问法是“可能”有2球颜色不同。我们不妨先拿出2个球,这两个球颜色有可能是2黑,也可能是2白,也可能是1黑1白,也就是只用拿出2个球就可能出现颜色不同的情况了。
问题(2)的问法是“保证”有2球颜色不同。如果我们只拿出2个球,有可能是2黑,也可能是2白,也可能是1黑1白,不能保证有2球颜色不同的情况一定发生。我们再考虑拿3个球的情况,有可能是3黑,也可能是2黑1白,也可能是1黑2白,也可能是3白,同样不能保证有2球颜色不同的情况一定发生。我们接着考虑拿4个球的情况,有可能是4黑,也可能是3黑1白,也可能是2黑2白,也可能是1黑3白,也可能是4白,同样不能保证有2球颜色不同的情况一定发生。我们再考虑拿5个球的情况,有可能是4黑1白,也可能是3黑2白,也可能是2黑3白,也可能是1黑4白,这样每种情况都有2个球的颜色不同,正好满足题目要求。所以,至少要从袋子中拿出5个球才能保证有2个球的颜色不同。
而最不利原则问题的典型问法就是问题(2)中的问法,题干中往往会出现“至少……才能保证……”的类似表述,求要保证某件事发生的最少情况数,这就是最不利原则的题型特征。
2.解题原则
上面我们是用枚举法找到满足“保证有2个球的颜色不同”的最少拿球的数量,但是用枚举法解决问题会比较麻烦。
这里我们不妨分析出最不利的情况,也就是刚好不满足题目要求的情况。题干要求有两个球不同色,所以最不利情况就是摸出的球颜色都相同。我们假设从拿出第一个球开始,后面拿出的球都是同色的,这样直到拿出第四个球后,四个球都是同色的,此时仍然不满足题目要求,这就是最不利的情况。而剩余的球都与拿出的4个球不同色,这样再拿一个球就一定能保证有2个球的颜色不同了。
所以最不利问题的解题思路就是:找到最不利的情况数,再加1就解决了问题。
【例题1】一个盒子里装有红球5个、黄球9个、蓝球12个,每次摸1个球放到盘子里,最少摸几次,才能保证一定有6个是同色的?( )
A.16 B.17 C.19 D.21
【答案】A【解析】根据题干中“至少……才能保证”判定是最不利原则问题。我们先找到最不利的情况数,要保证6个颜色相同,最不利的情况就是摸出的球最多都是5个同色,也就是红球、黄球和蓝球都先分别摸出5个球,这样再摸出1个球就能保证有6个球是同色的。所以最少摸球的次数为:5×3+1=16次,故本题选A。
【例题2】从一副完整的扑克牌中,至少抽出几张才能保证有三张相同花色?( )
A.9 B.10 C.11 D.12
【答案】C【解析】这道题要保证有三张花色相同,最不利的情况就是红桃、黑桃、方块和梅花这4种花色手里都分别有两张相同花色,再抽出大小王两张。那么再抽一张,就一定能保证和手里的某两张凑成一样花色的三张。所以最少抽牌的数量是:2×4+2+1=11张,故本题选C。
【例题3】梅花小区组织党员参与“两学一做”相关主题演讲、征文、摄影、书法和绘画五项比赛,要求每名党员参加其中的两项,无论怎么安排都发现至少有7名党员参加的培训内容完全相同,问小区至少有几名党员?( )
A.50 B.51 C.60 D.61
【答案】D【解析】从五项比赛中选择两项,没有顺序要求,所有的培训内容共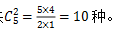 最不利的情况是每种培训内容都有6名党员参加,这样我们再加1名党员参加,就能保证至少有7名党员参加的培训内容完全相同。所以党员人数最少有:10×6+1=61名,故本题选D。
最不利的情况是每种培训内容都有6名党员参加,这样我们再加1名党员参加,就能保证至少有7名党员参加的培训内容完全相同。所以党员人数最少有:10×6+1=61名,故本题选D。
学会隔板模型 解决“至少分一个”难题
今天分享给大家在排列组合问题中十分常见的题型,即隔板模型。
在这里需要注意的是,此类隔板模型问题就是将n个相同元素分给m个不同的对象,每个对象至少分得1个,且没有剩余。则假设将n个元素一字排开,中间产生出n-1个空,用m-1个木板放入n-1个空中,就是分配方法的总数,即共有
这类问题模型适用前提相当严格,必须同时满足以下3个条件:
1.所要分的元素必须完全相同;
2.所要分的元素必须分完,决不允许有剩余;
3.每个对象至少分到1个,决不允许出现分不到元素的对象。
一、简单应用:题干满足隔板模型的所有条件
【例题】公司采购了一批同一型号的新电脑,总共11台,计划分给公司内的4个部门,每个部门至少分得一台,最终要将电脑分完,那么总共有多少种分配方法?( )
A.100 B.110 C.120 D.130
【答案】C【解析】这道排列组合题目中,同一型号电脑11台,即对应11个相同元素,分给公司4个部门即对应分给4个不同的对象,要求分配完且每个部门至少分1台,最终要分完,完全符合隔板模型,直接用公式得: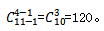
二、复杂应用:题干不满足模型的第3个条件,但是可以通过转换使之满足
【例题1】将15个完全相同的小球放入编号为1,2,3,4的四个盒子中,要求每个盒子中的小球数量不得小于其自身的编号数字,且不得有剩余的小球。那么有多少种分配方法?( )
A.48 B.56 C.64 D.72
【答案】B【解析】这个排列组合问题中,15个完全相同的小球即对应15个相同的元素,编号为1,2,3,4的四个盒子即对应四个不同的对象,且要求不得有剩余,唯一不符合我们给出公式的条件是,不是每个盒子里至少放一个小球,而是每个盒子的小球数量不小于其自身的编号,即1号盒子至少放1个小球,2号盒子至少放2个小球,以此类推,所以我们需要将条件转换。这里假设,1号盒子不动,给2号盒子先放1个小球,3号盒子先放2个小球,4个盒子先放3个小球,那么此时还剩9个小球,并且4个盒子都至少仍需要放一个小球,则此时条件符合使用公式,即将剩下的9个小球放入4个盒子中,每个盒子至少放一个小球,直接用公式得: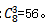 故本题选B。
故本题选B。
【例题2】教师节当天,某班级准备了8捧相同的花,送给4位老师,要求随意分,分完即可,共有多少种分配方法?( )
A.145 B.155 C.165 D.175
【答案】C【解析】这个排列组合问题中,显然8捧相同的花对应条件中8个相同的元素,4位老师对应4个不同的对象,分完即可表明没有剩余,但随意分意味着并不是每一位老师至少分得一捧花,有可能某老师并没有分到花,所以此时我们仍需要将条件进行转换。这里假设,这个班级又借来4捧花,现在就有12捧花,则此时如果按照每位老师至少分得1捧,最后再从每位老师手中收回一捧花,则既满足我们公式的条件,又没有改变分配结果。故相当于求将12捧花分给4位老师,每位老师至少分得一捧的情况数,直接用公式求得: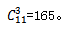 故本题选C。
故本题选C。








