
行测数量关系解题技巧
特殊题型隔板模型三步走
【第一步:识别题型特征】
什么是隔板模型?隔板模型是指“把n个相同的元素分给m个不同的对象,每个对象至少分到1个元素,问有多少种不同分法”这样的问题。
核心特征是:1.被分的元素必须完全相同;2.每个对象至少分到1个元素。符合这两个特征的题目,称为隔板模型问题。如:把10颗相同的糖果分给三个小朋友,每个人至少分得1颗,问有多少种不同的分法?要分的糖果相同,每个小朋友至少分得1颗,就满足隔板模型的条件。
【第二步:标准计算方式】
把n个相同元素分给m个不同的对象,每个对象至少分到1个元素,可以认为在n个相同元素的(n-1)个空隙中,插入(m-1)个隔板,这样就可以把元素分成m份,隔板的放法用组合数可以记作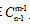 ,也就是说把n个相同元素分给m个不同的对象,每个对象至少分到1个元素,分法有
,也就是说把n个相同元素分给m个不同的对象,每个对象至少分到1个元素,分法有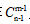 种。
种。
【例题】过年回家带了10份礼物,给爸妈家至少1份,爷爷家至少1份,伯伯家至少1份,问有多少种分法?
【答案】36种【解析】本题就是典型的隔板模型问题,符合所有特征,被分的元素为10,分给对象为3,则直接套用公式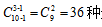 分配方案。
分配方案。
【第三步:变形则“化一”】
【例题】过年回家带了20份相同礼物,给爸妈家至少3份,爷爷家至少4份,伯伯家至少1份,问有多少种分法?
【答案】91种【解析】本题由题干信息可知,按照要求伯伯家至少1份,爸妈家至少3份,爷爷家至少4份,并不满足“每个对象至少分到1个元素”的条件,但如果把题干信息整理、变形来看,将20份礼物中的2份先给爸妈家,再给爷爷家3份,这时还剩下15份礼物,就相当于信息转化为“将剩余的15份相同礼物分给三家,要求每家至少1份礼物”,符合隔板模型问题所有特征,那么,应计为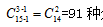 分法。
分法。
通过以上例题可以发现,要分相同元素给不同对象但题干条件不满足的情况下,可以通过“先分”和“先借”将题干条件转化为“每个对象至少分到1个元素”,进而用隔板模型解决。
了解完隔板模型的三步走,就会发现这类特殊的排列组合也可以快速掌握并有效解决,点滴积累,立志公成。
整除思想
【核心思想】
通过分析所求量的整除特性结合选项进行排除,从而选出正确选项。
【适用范围】
1.题干文字描述中出现“整除、每、平均、倍”等字眼;
2.数据体现“分数、百分数、比例”等数据。
【例题1】学校有足球和篮球的数量比为8:7,先买进若干个足球,这时足球和篮球的比变为3:2,接着又买进一些篮球,这时足球和篮球数量比为7:6.已知买进的足球比买进的篮球多3个,原来有足球多少?( )
A.48 B.42 C.36 D.30
【答案】A【解析】本题求的是原来的足球数量,即选项4个答案说的都是原来的足球数量,所以我们在求解的过程中可以只关心原来的足球数量,而在题目中与原来足球数量相关的只有这一句话:“学校有足球和篮球的数量比为8:7”,也就是说原来的足球无论有多少个,都可以被平均分8组,这样才可以达到和篮球“8:7”的比例,且足球数量必须是整数,故而得知足球总数必定被8整除,而我们选项中只有48可以被8整除,故本题选A。
【例题2】(2013国考)两个派出所某月内共受理案件160起,其中甲派出所手里的案件中有17%是刑事案件,乙派出所受理的案件中有20%是刑事案件,问派出所在这个月中共受理多少起非刑事案件?( )
A.48 B.60 C.72 D.96
【答案】A【解析】“甲派出所受理的案件中有17%是刑事案件”,案件数是正整数并且出现了百分数,所以考虑使用整除思想,因此由17%可知甲派出所受理总案件无论是多少件,都必须要能够分成100份,并且其中17份是刑事案件,因此,甲派出所总案件数必须是100的倍数,结合“共受理案件160起”可知甲派出所受理案件100起,乙派出所受理案件60起,再由“乙派出所受理的案件中有20%是刑事案件”可知乙受理非刑事案件占80%,因此所求为60*80%=48(起),故本题选A。
工程问题中多者合作问题怎么快速解答
【利用最小公倍数】
题目中出现多者独立完成工作的时间,那么我们就可以设他们独立完成工作时间的最小公倍数为工作总量,从而可以把他们相应的效率一一表示出来。
【例题】小刘的新房现要装修,甲师傅单独施工需要10天完成,乙师傅单独施工需要15天完成。若两位师傅合作施工,需要几天完成?( )
A.10 B.15 C.6 D.8
【答案】C【解析】方法一:设工程总量为w,共同工作所需时间为t,则甲、乙的效率为
方法二:已知甲、乙师傅单独施工分别需要10天和15天,可设工作总量w为他们时间的最小公倍数为30,则甲、乙的工作效率分别为3和2,那么他们合作完工需要30÷(3+2)=6天。
【利用效率之比】
如果题目给出多者之间的工作效率之比,那么我们就可以直接将各自效率的比值当作各自的效率去计算。
【例题】甲、乙、丙三个工程队完成一项工作的效率比为2:3:4。某项工程,乙先做了1/3后,余下的交由甲与丙合作完成,3天后完成工作。问完成此工作公用了多少天?( )
A.6 B.7 C.8 D.9
【答案】A【解析】方法一:甲、乙、丙的效率之比为2:3:4,则可设甲、乙、丙的效率分别为2p、3p、4p。由题意可得,甲丙合作3天完成了总量的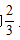 ,则工作总量为
,则工作总量为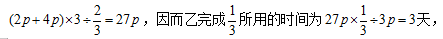 那么完成此项工程公用了3+3=6天。
那么完成此项工程公用了3+3=6天。
方法二:已知甲、乙、丙的效率之比为2:3:4,可直接将甲乙丙的工作效率当作2、3、4来处理。由题意可得,甲丙合作3天完成了总量的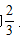 ,则工作总量为
,则工作总量为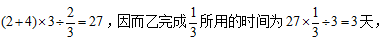 那么完成此项工程公用了3+3=6天。故本题选A。
那么完成此项工程公用了3+3=6天。故本题选A。
【利用效率相同设为单位“1”】
题目出现“每人”、“每台机器”等字样时,我们通常将“每人”、“每台机器”的效率当作“1”来处理,从而达到简化计算的目的。
【例题】修一条公路,假设每人每天的工作效率相同,计划180名工人1年完成,工作4个月后,因特殊情况,要求提前2个月完成任务,则需要增加工人多少名?( )
A.50 B.65 C.70 D.60
【答案】D【解析】方法一:设每人每个月的效率为p,增加的工人为x,则有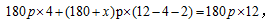 解得x=60。
解得x=60。
方法二:题目中出现了“每人每天的工作效率相同”,则可设每个工人每个月的效率为1,同时设需要增加x名工人,则有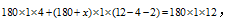 解得x=60名。故本题选D。
解得x=60名。故本题选D。
“和定最值”题型
【知识铺垫】
和定最值的核心:已知几个量的和一定,去求其中某个量的最值(最大值或最小值)。
解题的原则:要想求某个量的最大值就让其他量尽量小;要想求某个量的最小值就让其他量尽量大。
【例题1】已知两个不同的正整数之和为15,这两个数中较大的数最大为多少?( )
【答案】14【解析】假设这两个数按照编号为“一”最大,“二”最小,根据解题原则要想求最大的量尽量大,因为两数之和一定,故让另一个数尽量小,又第二个数字需满足为正整数,那么最小只能为“1”,则较大的数最大为15-1=14。
【例题2】某企业参与兴办了甲、乙、丙、丁4个扶贫车间,共投资450万元,甲车间的投资额是其他三个车间投资额之和的一半,乙车间的投资额比丙车间高25%,丁车间的投资额比乙、丙车间投资额之和低60万元。企业后期向4个车间追加了200万元投资,每个车间的追加投资额都不超过其余任一车间追加投资额的2倍,问总投资额最高和最低的车间,总投资额最多可能相差多少万元?( )
A.70 B.90 C.110 D.130
【答案】C【解析】题目已知四个车间最开始总投资为450万元,根据题目描述,假设甲车间所得投资额为x万元,则乙丙丁共得投资额为2x元。x+2x=450,则x=150;则乙丙丁车间投资额之和为300万;根据题目条件可设丙为y,则乙车间为1.25y,丁车间为2.25y-60;则有y+1.25y+2.25y=300,解得y=80,则各车间所得投资额如下图所示:
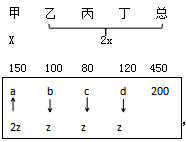
后期追加投资额为200万元,假设四车间所得投资额分别为a、b、c、d万元,且每个车间的追加投资额都小于等于其余任一车间追加投资额的2倍,以a为例:a≤2b,a≤2c,a≤2d。要想总投资额最大的车间和总投资额最小的车间相差最多,则需要让最开始得到投资额最多的车间得到追加的投资额最多,最开始得到投资额最少的车间得到追加投资额最少即可,丙车间原本最少,假设它追加投资额为z(即四车间最少得到追加投资额为z),甲车间原本最多,其追加投资额最多为2z。
根据和定最值解题原则:已知四个车间所得投资额之后为200万元,要想甲车间得到投资额2z尽量多,则乙丙丁的投资额尽量少,最少均为z,则有2z+z+z+z=200,z=40;则总投资额最大的车间和总投资额最小的车间相差最大为150+80-(80+40)=110万元,选C。
【例题3】某地10户贫困农户共申请扶贫小额信贷25万元,已知每户申请金额都是1000元的整数倍,申请金额最高的农户申请金额不超过申请金额最低农户的2倍,且任意2户农户的申请金额都不相同。问申请金额最低的农户最少可能申请多少万元信贷?( )
A.1.5 B.1.6 C.1.7 D.1.8
【答案】B【解析】将10户贫困户按照得到信贷从最高到最低编号为“一、二、......九、十”已知10户贫困户所得信贷总和为25万元。根据和定最值解题原则,要想求某个量的最小值就让其他量尽量大。求最低的农户(第十户)最少的金额,假设其为x万元,则金额最多的贫困户最多为2x万元。且每户金额均为1000元(0.1万)的整倍数且各不相同,则每家所得信贷金额如图所示:

则有2x+2x-0.1+2x-0.2+2x-0.3+2x-0.4+2x-0.5+2x-0.6+2x-0.7+2x-0.8+x=25,x=1.5X,因为本题1.5X为最小值,不能取比1.5X更小的数值,故取x=1.6。则本题申请金额最低的农户最少为1.6万元,故本题选B。
通过上面这两道题目可以总结出:首先,可以通过题目特征“已知几个量的和一定,求其中某个量的最值”判断出题型。其次,根据解题原则“要想求某个量的最大(小)值,就让其他量尽量小(大)”,结合表格和箭头方向呈现最大或最小值的情况解题。








