政华教育

【答案】B【解析】已知多个主体完工时间，通过特值法设工作总量为甲乙完工时间的最小公倍数120，由工作效率=工作总量÷工作时间可得，甲的效率为4，乙的效率为3，设丙的工作效率为x，则工作总量为：10×(3+4)+4×(3+4+x)=120，解得x=5.5，则丙单独完成该工程，需要120÷5.5≈21.8天，即需要22天，故本题选B。

二、已知多个主体效率关系时，根据效率关系将效率设为最简比的数值

【例题】甲工程队与乙工程队的效率之比为4：5，一项工程由甲工程队先单独做6天，再由乙工程队单独做8天，最后由甲、乙两个工程队合作4天刚好完成，如果这项工程由甲工程队或乙工程队单独完成，则甲工程队所需天数比乙工程队所需天数多多少天？（）

A.3 B.4 C.5 D.6

【答案】C【解析】根据题干甲乙工程队的效率之比为4：5，直接设甲、乙工程队效率分别为4和5，则总工作量=6×4+8×5+4×(4+5)=100，甲单独完工需要100÷4=25天，乙单独完工需要100÷5=20天，所求为25-20=5天。故本题选C。

三、已知多个主体效率相同时，设每个主体的效率为1

【例题】一批零件，有3台效率相同的机器同时生产，需用10天完成。生产了2天后，车间临时接到工厂通知，这批零件需要提前2天完成，若每台机器的效率不变，需要再投入多少台相同的机器？（）

A.1 B.2 C.3 D.4

【答案】A【解析】根据题干描述3台机器效率相同，将每台机器每天的工作效率设为1，则工作总量为1×3×10=30，生产两天后，剩余的工作量为30-1×3×2=24，又需要提前2天完工，则剩余工作量的完工时间就是10-2-2=6，因此剩余工作每天的工作效率为24÷6=4，由于每台机器每天效率为1，故需要再投入1台机器。故本题选A。

不定方程如何快速求解

计算问题是行测考试当中每年必考的题型，而不定方程又是计算问题当中常考的一类知识点。实际上，只要掌握一定的解题方法，不定方程也是可以快速求解的。不定方程是指当未知数的个数多于独立方程的个数时，这样的方程就称为不定方程，比如5x+6y=42，3x+2y+10z=52，这类题具体要怎么快速求解呢。

方法一 代入排除法：把选项代入题干当中，得出正确答案。

【例题】7x+9y=55，已知x，y为正整数，则x的值是：( )

A.2 B.4 C.5 D.7

【答案】B【解析】代入A选项，x=2时，即7×2+9y=55，9y=41，则y不是正整数，排除；代入B选项，x=4，即7×4+9y=55，9y=27，y=3，符合题干要求x，y为正整数；同理代入C，D求出y发现不符合题干要求，故本题选B。

方法二整除特性：未知数的某个系数与常数之间存在非“1”的公约数。

【例题】3x+7y=33，已知x，y为正整数，则x+y=( )

A.11 B.10 C.8 D.7

【答案】D【解析】对于这一道题我们发现带入四个选项都去试验并排除错误选项会浪费时间，那我们可以在这个基础上找到一些方法快速地排除或确定某选项。观察常数项33和未知数x的系数3存在公约数3，即3x为3的倍数，33为3的倍数，故7y为3的倍数，而7不是3的倍数，所以y为3的倍数，当y为3的时候，x为4符合题意，则x+y=7，故本题选D。

方法三奇偶性：未知数前的系数为一奇一偶。

【例题】双十一期间小王在网上买了16元一袋的纸巾、10元一支的牙刷和7元一瓶的洗手液若干，共花了156元，如果他买的每一样物品数量都不相同。纸巾数量最多而洗手液最少，那么他买的牙刷数量比洗手液多几个？（）

A.1 B.2 C.3 D.4

【答案】A【解析】设买纸巾、牙刷、洗手液的数量分别为x、y、z，则16x+10y+7z=156(x>y>z)，由于16x、10y和156都为偶数，所以可知z必须为偶数，代值检验，当z=2时，16x+10y=142，化简为8x+5y=71，8x为偶数，71为奇数，则5y为奇数，5为奇数，则y为奇数，又因为y>z，z=2，则y最小为3，当y=3时，x=7，符合题意，牙刷数量比洗手液多1个。故本题选A。

方法四尾数法：未知数前的系数以“0”或“5”为结尾。

【例题】已知周某生日的月份数乘以2，加上10，再把和乘以5，加上他家人数，结果是143。如果周某家人数不到10人，则他的生日在几月？（）

A.9 B.10 C.11 D.12

【答案】A【解析】设周某生日的月份数和周某家人数分别为x，y，则有5×(2x+10)+y=143，整理得10x+y=93。10x的尾数为0，93的尾数为3，所以y的尾数为3。由于y<10，那么y只能取3，则x=9。即周某生日在9月。故本题选A。

巧设未知数列方程

在行测数量关系中，计算问题是无疑高频考点之一了，利用方程法解决计算问题是我们在平时练习过程中经常会遇到的，然而在同一道题目中，所设未知数不同、设法不同，可以列出很多种不同的等量关系，但在解方程过程中计算难度却天差地别。

【结合分母设未知数】

【例题】某班学生在一次考试中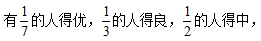，得中的人数比得优、得良的人数之和多2人。

在这个例子中存在的等量关系应该不难发现，就是得中的人数-得优、得良的人数=2。如果将总人数设为x，从而就能表示出得优的人数为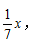良的人数

列出方程之后大家会发现出现多个分数，求解过程中需要进行通分，相当于要多进行一步计算，那么为了避免复杂计算，不妨结合多个分数的分母，设总人数为42x(42为2、7、6的最小公倍数)，那么得优的人数为6x，得良的人数为14x，得中的人数为为21x，从而得到方程：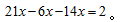

以上根据同样条件列出的等量关系，在求解过程中难度高下立判，所以如果题干出现多个分数，且都是占某个整体的比重时，我们可以结合条件，先将分母最小公倍数求出来再进行设未知数列式。

【结合比例关系列方程】

如果题干中出现一些比较明显的比例关系时，可以结合比例系数设方程，具体通过例2进行说明：

【例题】某高校艺术学院分音乐系和美术系两个系别，已知学院男生人数占总人数的30%，且音乐系男女生人数之比为1∶3，美术系男女生人数之比为2∶3。问音乐系和美术系的总人数之比为多少？

A.2∶1 B.3∶2 C.3∶1 D.5∶4

【答案】A【解析】本题已知音乐系男女人数比为1∶3，可以结合比例关系设音乐系男女人数分别为x和3x，同理，结合美术系男女生人数之比为2∶3，设美术系男女人数分别为2y和3y。由学院男生人数占总人数的30%可得等量关系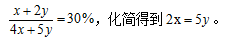题目所求为音乐系和美术系的总人数之比，即求4x∶5y=10y∶5y=2∶1，根据选项可知，故本题选A。

快速解决不定方程问题之赋值法

行测考试数量关系类题目考察的比较多。不定方程也属于近年来比较常见的一类题目，那么怎么把不定方程问题做的又快又好呢？下面就带大家来学习其中的一种方法——赋值法。

首先，未知数的个数多于独立方程的个数，这样的方程(组)我们称之为不定方程，例如：

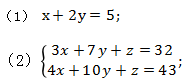
那我们今天学习的方法，主要是针对于第二种形式的方程组进行求解，下面我们通过一道例题来说明。

【例题1】甲、乙、丙三种货物，如果购买甲3件、乙7件、丙1件需花3.15元；如果购买甲4件、乙10件、丙1件需花4.2元，那么购买甲、乙、丙各一件需要花多少元钱？（）

A.1.05 B.1.4 C.1.85 D.2.1

【答案】D【解析】根据题意，可以设甲1件为x元、乙1件为y元、丙1件为z元，得到一个方程组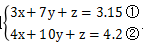，由于方程组含三个未知数，但只有两个独立方程，所以x，y，z可能有多组解，想要求解“x+y+z”为多少，我们可以采取以下两种方法。

方法一：通过两个式子整体运算，整理出x+y+z。可以将式①×3-式②×2恰好得到“x+y+z=1.05”，即A选项。

方法二：由方程组我们是可以得到无数组的解，但题目是单选题，意味着x+y+z的答案是唯一的，所以可以通过任意一组解来确定这个整体的值。为了方便计算，我们不妨假设系数最复杂的未知数y=0，可以得到方程组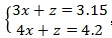，不难解出x=1.05、z=0，可得“x+y+z=1.05+0+0=1.05”，故本题选D。

对比以上两种方法，在实际考试中如果想用第一种办法，需要我们有较强的数字敏感，仔细认真的观察每个方程的系数特点；而方法二操作起来会更简单，考场上也不会浪费我们太多时间，这就是我们今天主要学习的赋值法。使用时大家要注意，只有在求整体时我们才用赋值法，想求其中某一个量具体值时是不适用的，解题时可以将系数最复杂的未知数设为零，再联立剩下的方程求解即可。

【例题2】木匠加工2张桌子和4张凳子共需要10个小时，加工4张桌子和8张椅子需要22个小时。如果他加工桌子、凳子和椅子各10张，共需要多少个小时？（）

A.47.5 B.50 C.52.5 D.55

【答案】C【解析】设木匠加工1张桌子、1张凳子、1张椅子所用时间分别为x、y、z小时，根据题意有2x+4y=10，4x+8z=22，令x=0，可解得y=2.5，z=2.75，则所求为(0+2.5+2.75)×10=52.5小时。