政华教育

【答案】B【解析】65名毕业生分配到7个部门，行政部门分的最多，并且要尽可能少，由于人数和为定值，其它六个部门人数要尽可能多。假设行政部门为x人，由于本题其他部门人数可以相同，则其它部门最多为(x-1)，则x+6(x-1)=65，解得x≈10.1，x取正整数，并且不能小于10.1，因此取11，根据选项可知，本题选择B项。

例3:从某物流园区开出6辆货车，这6辆货车的平均载重为62吨，已知每辆货车装载量各不相同且均为整数，最重的装载了71吨，最轻的装载了54吨。问：这6辆货车中装载第三重的货车至少装载了多少吨（）？

A.59 B.60 C.61 D.62

【答案】B【解析】6辆货车的平均载重为62吨，则总重量为6×62=372，第三重的货车至少装载了多少吨，由于总的装载量为定值，则其它货车装载量要尽可能大，最大的题目已知是71，则排第二最大为70，设排第三装载为x，由于每辆货车装载量各不相同，则第四最多为x-1，第五最多为x-2，第六已知为54，则71+70+x+x-1+x-2+54=372，解得x=60，根据选项可知，本题选择B项。

通过上面三道题目的学习，了解了常见的和定最值的题型特点和求解方法。在求解某个量的极值时，由于和为定值，求解这个量要最大，其它量要尽可能小；如果求解这个量要最小，其它量要尽可能大。在分配数据时有时要辅助的设未知量，求出的未知量如果不是正整数，在取值时要根据极值问题本身要求取舍，而不是套用四舍五入取舍。

行测数量关系巧解工程问题中的交替合作的问题

在行测数量关系中，工程问题尤为重要，而工程问题中常考的，又相对比较难的就是交替合作。今天就为大家分享一下解交替合作的方法。

什么是交替合作

多个人合作完成某一项工程，但是在合作的过程中这些对象都是按照一定的规律循环完工。例如：某项工程，甲单独完工作完成需要3天，乙单独完成需要2天；甲做一天，乙做一天，甲做一天，乙做一天……按照这样的方式如此重复下去。这道题中出现的“甲做一天，乙做一天，甲做一天，乙做一天……”就是甲乙工作的循环规律，而出现以一定循环规律工作的题目就是交替合作。

解题核心关键

找到最小循环周期，再求出一个周期内的工程量之和。

解题步骤

1.求出工程总量和各自单独的效率。

工程总量或各自的效率一般没有单独给出，需要通过设特值来帮助解题。

若给出的是各个工作对象得完工时间，可设这多个完工时间的最小公倍数为工作总量。若给出的是各个工作对象的效率最简比，可设最简比为份数。

2.找到最小循环周期，并且求出一个周期内的工程量之和。

3.求出周期数。

周期数=工程总量/一个周期内的工作量之和

4.按照题意安排好不足一个周期的工作(若完工时刚好是完整周期，则不用考虑此步)。

5.求出完工时间。

例1:有一个图书馆的图书需要登记，已知甲登记这些书需要10天，乙需要15天。如果双方每人一天轮流登记，从甲开始开始，则一共需要( )天可完成。

A.10 B.12 C.14 D.16

【答案】B【解析】按照解题步骤，先把工作总量设为若干时间的最小公倍数W=30，则可求出甲的效率为3，乙的效率是2。由题意“双方每人一天轮流登记”，可求出一个循环周期的工作时间为2天，一个循环周期的工作量为5，由30÷5=6，这批图书需要6个完整的循环周期可以完成。求出时间6×2=12天。选B。

例2:有一个图书馆有240本书需要登记，已知甲登记这些书需要10天，乙需要12天。如果从甲开始双方每人一天轮流登记，则大约需要( )天可完成。

A.10 B.11 C.12 D.13

【答案】B【解析】按照解题步骤，工作总量为240，可求出甲的效率为24，乙的效率为20。由题意“双方每人一天轮流登记”，可求出一个循环周期的工作时间为2天，一个循环周期的工作量为20+24=44，由240÷44=5……20可知，5个周期后，还剩20本书未登记完。前5个周期用时5×2=10天，还剩20本书则再开始一个循环，由甲开始，甲登记一天可登记24本书，剩下得20本书只需呀20÷24≈0.83天，因此完成这项图书登记工作需要10+0.83=10.83≈11天。选B。

由上面两个题我们发现只要记住了交替合作的解题步骤，那么此类题很好拿分。

行测数量未解之谜——为什么要边注水、边放水？

有这样一道奥数题难道了众多考生：比如“有一个蓄水池，如果往里面注水，3小时注满；如果往外放水，4小时放干。请问管理员同时注水和放水，几小时可以把水池注满？”这类边放水边注水的题目是很多小学奥数会学习的内容，我们公务员考试的数量关系也会涉及到。其实我们学习这类题目是帮大家培养一种思维，抽象的数学模型能帮助我们更方便去研究这类题目。比如我们生活中手机边使用边充电、下雨时蓄水池放水多久能放到安全水位等等，其实就是对这一类题目的应用。当然我们在进行题目设定的时候也要注意要符合生活实际。接下来就和大家一起做一下类似的题目吧。

青蛙跳井展示

例题1:现有一口高10米的井，有一只青蛙坐落于井底，青蛙每次跳的高度为5米，由于井壁比较光滑，青蛙每跳5米下滑2米，请问，这只青蛙几次能跳出此井（）？

A.1 B.2 C.3 D.4

【答案】C【解析】青蛙跳井问题可以看做是工程问题，向上跳看做正效率，往下滑看做负效率。青蛙每跳5米下滑2米，相当于青蛙一次只能上升3米，跳2次后离井口还有4米，此时再跳一次就直接出去了，所以总共跳3次，选C项。

【思维点拨】我们重新梳理一下这个解题过程，由于最后一次是向上跳跃的过程，那我们可以在10米深度基础上先减去一次向上跳跃的距离，剩下的距离只需要跳跃若干次就可以跳出去了。这样就变成了(10-5)÷(5-2)=1.X次，向上取整为2次，到达距离距离井口小于5米的地方。这样再跳一次就可以出去了，所以一共跳跃2+1=3次，就可以跳出井口到达地面。

同类题目展示

例题2:一个车站有A1和B2两个进站口，一个出站口，单开A1口6小时达到最大客流量；单开B2口5小时达到最大客流量；客流量最大时单开出站口3小时清空车站。早上车站没有人，如果按照A1、B2、出口的顺序循环轮流开放，每个口每次只开放1小时，那么经过多少个小时后车站达到最大客流量（）？

A.59 B.60 C.79 D.90

【答案】A【解析】方法一：设工作总量为30，则A1、B2、出口的效率分别为5、6、-10，三小时看做一个周期，一个周期的效率和为1，19次循环后，还剩11个工作量没完成，接下来A1、B2各1小时，车站达到最大客流量。19个周期对应57小时，所以共需59小时，选A项。方法二：设工作总量为30，则A1、B2、出口的效率分别为5、6、-10，三小时看做一个周期，一个周期的效率和为1，(30-5-6)÷(5+6-10)=19个周期，接下来A1、B2各1小时，车站达到最大客流量。19个周期对应57小时，所以共需59小时，选A项。

通过上面的例题，相信大家对这类题目也有所了解，希望大家能够多加练习，提高做题的速度和效率，在考试中取得好成绩。

2022省考行测备考：年龄问题你会了吗？

在公务员行测考试中，数量关系是行测考试中的重要部分，大部分考生都认为在考试时间有限的情况下难度比较大，不会做。其实也有简单的题，比如年龄问题整体难度不大，解题核心单一，在备考中建议考生熟练掌握。接下来带领大家学习解决年龄问题的核心及方法。

什么是年龄问题

年龄问题是研究两人或者多人之间的年龄变化和关系的问题。

年龄问题的核心

1.年龄同增同减：每过一年，所有人都增长一岁。

2.年龄差不变：每过N年，每个人的年龄均增长N岁，也就是任意两人的年龄差不变。

常用方法

1.方程法：题干描述比较简单，等量关系比较明显。

2.列表法：题干描述比较复杂，等量关系不太明显。

例1:办公室有甲、乙、丙、丁4位同志，甲比乙大5岁，丙比丁大2岁。丁三年前参加工作，当时22岁。他们四人现在的年龄之和为127岁。那么乙现在的年龄是( )。

A.25岁 B.27岁 C.35岁 D.40岁

【答案】C【解析】设乙现在的年龄是x岁，则甲现在的年龄是x+5岁，丁现在25岁，丙现在27岁，则有x+5+x+27+25=127，解得x=35，所以乙现在的年龄是35岁。选择C选项。

例2:3年前张三的年龄是他女儿的17倍，3年后张三的年龄是他女儿的5倍，那么张三的女儿现在：( )。

A.2岁 B.3岁 C.4岁 D.5岁

【答案】D【解析】设女儿现在的年龄为x岁，列表如下：

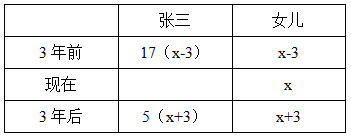
根据张三和女儿的年龄差不变，有17(x-3)-(x-3)=5(x+3)-(x+3)，解得x=5，则女儿现在的年龄为5岁。选择D选项。

例3:甲乙两人年龄不等，已知当甲像乙现在这么大时，乙8岁；当乙像甲现在这么大时，甲29岁。问今年甲的年龄为多少岁（）？

A.22岁 B.34岁 C.36岁 D.43岁

【答案】A【解析】设甲今年x岁，乙今年y岁，列表如下：

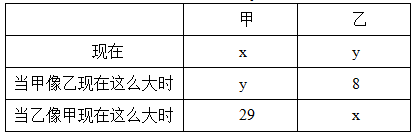
根据甲和乙年龄差不变，有x-y=y-8=29-x，解得x=22，故今年甲的年龄为22岁。选择A选项。

通过以上例题，我们知道年龄问题解题核心也就是年龄同增同减、年龄差不变，在做题过程中，简单题型可以直接通过方程法构建等量关系解题，复杂题型可以通过列表法梳理各个人物不同年份年龄之间的关系，结合方程法构建等量关系解题，大家掌握了吗？