行测数量关系备考技巧

行测数量关系：利润问题是你的强项吗

利润问题是行测考试中一类算钱的问题，所以要想掌握这类题型，就必须对钱的交易过程了如指掌。在做生意时，我们知道必须先买回来商品，才能再通过销售赚钱，所以在买东西进货时就有了第一个概念叫成本，也或者叫进价，而当商品进行销售时，就需要再定一个价格，故将其称为售价，因此售价成本之间的差价，就被称为利润。而当各位考生想要入手解决利润问题时，就必须对下列公式烂熟于心：

1.利润=售价-成本=成本×利润率。

2.利润率=(利润÷成本)×100%=(售价-成本)÷成本=售价÷成本-1。

3.成本=售价-利润=售价÷(1+利润率)。

4.售价=成本+利润=成本×(1+利润率)。

5.销售额=单价×销量。

6.打折率=(折后售价÷折前售价)×100%。

当你已经将上面的公式收入囊中后，接下来就带着它们练练手，提升一下解题技能吧！

技能一：公式法

例1：某商店两件商品售价相同，都为200元。一件商品盈利25%，一件商品亏损20%，则两件商品各售出一件时，盈利或亏损情况如何（   ）？

A.盈利5元        B.亏损5元         C.盈利10元        D.亏损10元

【答案】D【解析】第一件商品售价为200元，利润率为25%，可通过成本=售价÷(1+利润率)求得成本=200÷(1+25%)=160元，则第一件商品利润=售价-成本=200-160=40元；第二件商品售价为200元，利润率为-25%，可通过成本=售价÷(1+利润率)求得成本=200÷(1-20%)=250元，则第二件商品利润=售价-成本=200-250=-50元，两件商品共得利润=40-50=-10元，故亏损10元，答案选D。

技能二：方程法

例2：某商店5月份销售一台电脑的利润率是20%，6月份在之前价格基础上打九折销售，最终6月份每台电脑获利500元，问该电脑成本是多少元（   ）？

A.4750元          B.5550元         C.6250元          D.8050元

【答案】C【解析】假设每台电脑成本是X，则5月份电脑售价=成本×(1+利润率)=X(1+20%)=1.2X，6月份电脑售价=5月份售价×打折率=1.2X×0.9=1.08X，由利润=售价-成本可知，500=1.08X-X=0.08X，解得X=6250，故电脑成本为6250元，答案选C。

技能三：特值法

例3：某商店采购一批电视，先按30%的利润销售60%的商品，之后剩下商品打八折出售，问全部销售完毕后这批电视的利润率是多少（  ）？

A.18.6%     B.19.6%      C.20.8%      D.21%

【答案】B【解析】本题所求利润率=(利润÷成本)×100%，题目中利润和成本都不知道，可以设特值进行求解。一般设成本进行特值，本题还涉及到销量，同样没有具体数值，也可用特值进行代替。将成本设为100，销量设为10，用表格将题干信息进行梳理：

得利润率=(利润÷成本)×100%=[(30×6+4×4)÷(100×10)]×100%=19.6%，答案选B。

同学们拿到类似例三的题目时，可以结合问法，找到需要求解什么样的数据，再把特值设出来，进而方便计算过程。

以上的三种技能可以帮助同学们在利润问题的学习中得心应手，因此各位同学在解决利润问题时，要先弄清楚题干给了哪些量，再结合相关公式进行求解，如果某些量未知可用方程法设未知数进行解答，而对于一些可以使用特值法的题型，需要同学们熟练掌握公式法和方程法的基础上再进行提高。

行测指导：如何让自己成为“赌神”

在生活中我们遇到各种各样的“赌博”，当然这里的“赌博”并不是违法乱纪的“赌博”。我们生活中有各类竞技比赛，如田忌赛马，国足出线胜率等。在这些博弈中如何安排战术让自己获得最大胜率，立于不败之地就显得尤为重要。那么这就涉及到咱们行测的概率问题了。今天一起来学习一下概率问题中的多次独立重复实验问题知识点吧。

一、独立重复实验的定义

独立重复试验，又称为伯努利试验，是指在同样的条件下可以重复进行，且每次之间相互独立的一种试验。在每次试验中，某事件发生的概率都是一样的，彼此之间互不影响，且试验结果只有两种：事件要么发生，事件要么不发生。

二、独立重复实验公式

进行n次独立重复试验，每次试验中事件A发生的概率为p，A不发生的概率为(1-p)，则事件A共发生k次的概率：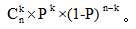

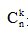是指从n次实验中将发生的k次选出来；事件A每发生一次概率为p，k次则为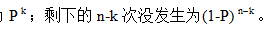

例1：根据天气预报，未来4天中每天下雨的概率均为0.6，则未来4天中仅有1天下雨的概率p为(    )？

A.0.03＜p＜0.05      B.0.06＜p＜0.09     C.0.13＜p＜0.16     D.0.16＜o＜0.36

【答案】C【解析】根据题意，为独立重复试验，直接代入独立重复试验计算公式，所求概率为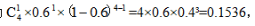选择C项。

例2：某次乒乓球比赛三局两胜，甲乙比赛，甲每局胜率0.8，问比赛中甲最终胜出的概率是多少（   ）？

A.0.768          B.0.8         C.0.896        D.0.924

【答案】C【解析】甲最终获胜，包括2：0与2：1两种情况。若为2：0，则甲连胜两局，概率为0.8×0.8=0.64；若为2：1，则共打三局，前两局甲一胜一负，且第三局甲胜，概率为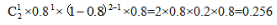：因此，所求的比赛中甲最终胜出的概率为：0.64+0.256=0.896，选择C项。

例3：甲和乙两名水平相当的选手打羽毛球，每局每人的胜率都是50%，如果两个人打五场，甲至少连胜三场的概率为∶（   ）

A.1/4        B.1/8       C.1/16       D.3/16

【答案】A【解析】根据比赛次数分类，两人连打五场，甲连胜三场，则甲连胜前三场、中间三场、后三场，前三场和后三场连胜的概率均为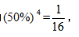中间三场连胜的概率为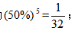甲连胜四场，则甲连胜前四场、后四场，概率均为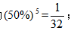甲连胜五场概率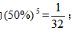为故所求为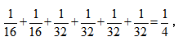故答案为A。

总而言之，关于多次独立重复实验问题要根据上述公式来对应题目求解，那么多次独立重复实验问题就轻而易举的解答出了。建议大家学会多次独立重复实验问题，这样就可以轻松在博弈中成为“赌神”。

行测数量关系：巧用排列组合隔板模型

对于行测数量关系中的排列组合题目，很多同学觉得很难，读完题目后没有解题思路，其实排列组合问题中有一类隔板问题，它可以按母题所给的公式模板套用到子题中，使复杂的问题简单化从而迎刃而解，最终把分数牢牢掌握在自己手中。首先我们做一道母题学习公式模板：

例1：9个一样的苹果分给3个小朋友，每个小朋友至少分得1个苹果，，共有多少种不同的分配方法？

【解析】既然要分给3个小朋友，不妨先把9个一样的苹果分成三堆，每一堆苹果对应给1个小朋友。先把9个苹果分开，苹果互相之间形成了8个空位，发现在8个空位中插进2块隔板，恰好把苹果分成三堆，同时无论怎样在8个空位中选择2个空位插板子，都保证了三堆里每堆至少有一个苹果，满足题中每个小朋友至少分得1个苹果的条件，故分配方式一共为种分配方式。结合此题，我们把它总结成公式，即Cm-1 n-1(m为小朋友数，n为苹果数)。

接下来我们对隔板模型的知识点进行拓展学习：

例2：9个一样的苹果分给3个小朋友，每个小朋友至少分得2个苹果，，共有多少种不同的分配方法？

【解析】先给每个小朋友1个苹果，此时还剩9-3×1=6个苹果，即题目转化为求“6个一样的苹果分给3个小朋友，每个小朋友至少分得1个苹果”的分配方法，在6个苹果间产生的5个空位中插入2块隔板，共有种分配方式。

例3：9个一样的苹果分给3个小朋友，任意分，共有多少种不同的分配方法？

【解析】“任意分”相当于每个小朋友至少分得0个苹果，可考虑先借后还，假设发放者先向每个小朋友借1个苹果，并保证在后续分苹果的过程中把借过来的苹果都还给小朋友们，那么这个问题就转化为：把9+3=12个苹果分给3个小朋友且每人至少拿1个苹果，利用公式，有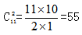种分配方式。

行测数量关系：攻克“整除”大山

很多同学在为2022年的省考做准备，而无论是国考还是省考，数量关系都成为大家心里的高岭之花——高不可攀，行测中数量关系的题目难度系数有点高，而数量关系又占据了不少的分数，成为大家学习弃之可惜的问题，那么如何才能学好数量关系的题目呢？大家需要做的就是放平心态，不要把它当成无法攻克的大山。学习数量关系是个循序渐进的过程，不能一蹴而就，要逐一突破。今天就带着同学们从基础的整除这一部分开始学习。

在整除这一部分，我们首先需要知道什么叫整除？若一个整数a除以一个非零整数b，商为整数，且余数为零。即a能被b整除，如35能被7整除。

除此之外需要去记住一些常见数字的整除判定，分别从整体和局部进行划分。

从整体看

1.作和：对于3和9来说，我们判断一个数能否被3或9整除，指这个数各项数位进行加和，通过和是否被3或9整除来判断。

2.作差：对于7和11还有13来说，我们可以通过分割作差法进行整除判定，将数值分割成两部分，后三位为一个数值，前面剩余部分为另一个数值，然后用大数减小数，得到的差值看是否是7或11或13整数倍，进而去判定整除。

在这里，11这个数字的整除判定除了可以利用分割作差判定，还可以利用间隔作差法，即将这个数值所有奇数位数字进行加和得到一个数值，再将所有偶数位上的数字进行加和得到一个数值，将两个加和得到的数值进行作差，用大数减小数，看差值是否是11的倍数，进而判断11的整除。

从局部看

1.2和5的整除判定，看数字的末一位。

2.4和25的整除判定，看数字末两位，即末两位能否被4或25整除。

3.8和1255的整除判定，看数字的末三位，即末三位能否被8或125整除。

合数

可通过因式拆分进行判断，如6=2*3，6的整除需同时满足2和3的整除条件。

在整除这一部分学习中，大家更关注的是什么时候能应用。即通过词句描述判定如：平均、每或整除字样出现。

例1：某班级发放课外书，平均每人能分到7本。后来该班级又转来若干学生，这样每人能分到6本，该班级课外书总数是(       )。

A.180元        B.210本       C.240本          D.280元

【答案】B【解析】由题意可知，课外书总数=7×班级原人数=6×班级现人数，则课外书总数是7和6的倍数，选项中只有B符合。

还可以通过数据呈现形式，如带有分数、比例、百分数、倍数等数据呈现。

例2：两个派出所某月内共受理案件160起，其中甲派出所受理的案件中有17%是刑事案件，乙派出所受理的案件中有20%是刑事案件，问乙派出所在这个月中共受理多少起非刑事案件（  ）？

A.48            B.60        C.72         D.96

【答案】A【解析】已知甲派出所的刑事案件占17%=17/100，根据整除特性可知甲派出所受理案件总数是100的倍数，又因甲、乙两派出所共受理案件160起，故甲派出所受理案件总数只能为100，则乙派出所受理案件总数为60，在这个月中共受理的非刑事案件数60×(1-20%)=48起。

以上内容只是针对整除问题的简单梳理，同学们要不断加强练习并进行总结才能熟练应用。最后希望各位同学们都能得偿所愿，含泪播种的人一定能含笑收获，加油！