政华教育

在公务员考试中，排列组合问题属于常考题型，有些考生觉得这类题有难度，不知道从何处入手。今天，我们就来了解一种常用的解题方法——捆绑法。题干通常会有元素是被要求相邻的，在求解的时候可以先把要求相邻的元素看成一个整体，再和其他元素一起进行安排，最后考虑捆绑起来的元素的位置安排。接下来通过例题来感受一下。

例1：四年级三班举行六一儿童节联欢活动，整个活动由2个舞蹈、2个演唱和3个小品组成。如果要求同类型的节目连续演出，那么共有多少种不同的出场顺序（）？

A.186 B.168 C.144 D.125

【答案】C【解析】由题意可知，同类型的节目要连续演出，所以相同类型的节目顺序不能随意安排，为了保证相邻可以先将相同类型的节目捆绑在一起看成一个整体，这样无论怎么摆放，相同类型的节目一定会相邻，一共得到三个整体，考虑三个整体的顺序安排，整体共有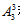种排列方法。最后考虑各种类型节目内部的顺序安排，分别有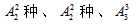种排列方法，因此所求为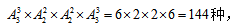故选择C。

例2：某场科技论坛有5G、人工智能、区块链、大数据和云计算5个主题，每个主题有2位发言嘉宾。如果要求每个主题的嘉宾发言次序必须相邻，则共有多少种不同的发言次序（）？

A.120 B.240 C.1200 D.3840

【答案】D【解析】根据题干要求，每个主题的嘉宾发言必须相邻，所以可以把每个主题的嘉宾捆绑成一个整体，5个主题5个整体，考虑5个整体之间的顺序安排，共有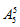种排列方法；最后考虑每个主题中的2位嘉宾发言的顺序安排，因此每个主题的两个嘉宾发言均有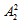种，则所求为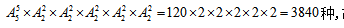故选择D。

以后我们碰到此类排列组合问题，只要题干中出现“相邻”字眼，我们就可以利用上面例题所讲述的方法进行求解，先将要求相邻的元素捆绑起来看成一个整体，然后和其他的元素一起进行位置安排，最后考虑捆绑元素内部的顺序安排。不积跬步无以至千里，不积小流无以成江海。备考过程既是对身体的挑战，也是对心理的考验，只有夯实每一个知识点，才能在考场上从容应对，真正的笑到最后。

行测技巧：公车问题——发车间隔

各位小伙伴大家好。公车问题是行测科目中数量关系的考点之一，其题型包括发车间隔和发车相遇问题两种，往往让很多同学束手无策。但是各种题型的解题方法又相对单一，只要掌握对应的公式或技巧就可迎刃而解。今天就和大家总结一下发车间隔问题的题型及相应解法，希望能帮助同学解决这一问题。

基本结论

题型：某人匀速行走在一条公路上，公路的前后两端每隔相同的时间发一辆公共汽车。他发现每隔A分钟有一辆公共汽车追上他；每隔B分钟有一辆公共汽车迎面驶来擦身而过。问公共汽车每隔多少分钟发车一辆？像这样一种求两辆车的发车间隔时间的问题，就是发车间隔问题。

结论：发车时间间隔=2×相遇事件时间间隔×追及事件时间间隔÷(相遇事件时间间隔+追及事件时间间隔)即发车时间间隔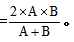

结论推导

例题：小明放学回家，他沿一路电车的路线步行，他发现每隔6分钟，有一辆一路电车迎面开来，每隔12分钟，有一辆一路电车从背后开来，已知每辆一路电车速度相同，从终点站与起点站的发车间隔时间也相同，那么一路电车每多少分钟发车一辆（）？

A.8 B.9 C.10 D.11

【答案】A【解析】沿一路电车的路线步行，每隔12分钟，有一辆一路电车从背后开来，这种情况具有以下特点：人车方向相同，是个追及问题；人所在位置与前一辆车相同，和下一辆的距离就是两车的发车间隔，下一辆车想追上人，那么就要比人多走这个发车间隔。这时，人车距离=发车间隔=追及距离=(车速-人速)×追及时间，其中追及时间常说成过多少分钟从后面来了一辆车。公式表示为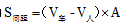(A为追及时间)。

沿一路电车的路线步行，每隔6分钟，有一辆一路电车迎面开来，这种情况具有以下特点：人车方向相反，是个相遇问题；人所在位置与前一辆车相同，和下一辆的距离就是两车的发车间隔，人车相遇，合走发车间隔。这时，人车距离=发车间隔=相遇距离=(车速-人速)×相遇时间，其中相遇时间常说成过多少分钟迎面来了一辆车。公式表示为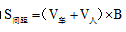(B为相遇时间)。

联立以上两个式子，得出，所以发车间隔为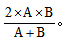代入结果为8分钟。故本题选A。

所以，以后我们在遇到发车间隔问题，就可以直接采用公式来解决。

通过这次学习，同学们需要理解例一中的基本原理，对比记忆。在之后碰到此类问题及其变形问题，把握核心原理，自然就可以解决。希望同学们能够熟练的掌握这种方法，攻克发车间隔问题这一难题！

常考点之利润问题由难化简

利润问题作为公考的一大重要考点，考生们一定都不陌生，对于利润问题大家费解的无非就是题干冗长，不知如何下手。但实际上利润问题无非就是研究交易之间的买卖关系，接下来和各位考生共同探索如何将利润问题由不易变容易。

首先，要对利润问题的公式熟记于心。虽然公式看似复杂，但实际上我们可以将利润问题的公式与增长的公式比对来记，这样能更容易理解。

记住公式以后，我们来看下面几道例题。

例1：某房地产公司分别以80万人民币的相同价格出售两套房屋。一套房屋以盈利20%的价格出售，另一套房屋以盈利30%的价格出售。那么该房地产公司从中获利约为：（）

A.31.5万元 B.31.6万元 C.31.7万元 D.31.8万元

【答案】D【解析】首先我们来分析一下题干所求，“从中获利”指的即为利润，那题干中都有哪些已知量呢？“分别以80万人民币的相同价格出售两套房屋”，由此可以看出，题干中给我们的就是房屋的出售价格，即为售价，均为80万人民币，“分别盈利20%和盈利30%”即为利润率，已知售价和利润率，想要求出利润，根据公式可知，利润=售价-成本，要想求出利润，必先求出两套房屋的成本，根据公式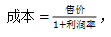：可分别求出，房屋1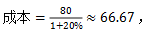房屋2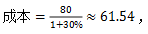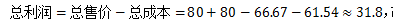故选D。(注：很多考生在遇到不能整除的问题当中不知应该具体保留几位有效数字，此时我们为了既能节省时间，又能提高准确率，可以结合选项，比选项多保留1位有效数字即可)

例2：某商店的两件商品成本价相同，一件按成本价多25%出售，一件按成本价少13%出售，则两件商品各出售一件时盈利为多少（）？

A.6% B.8% C.10% D.12%

【答案】A【解析】同上道题一样，我们首先要清楚题干所求，为两件商品各出售一件的利润率，但是题干所给信息均为单间出售时的利润率，这时我们来回想利润率公式：利润率=利润/成本，但题干中并未给我们其他任何信息，此时我们不妨将成本设为未知数x，可列出下表：

根据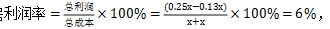故选A。

我们发现所设未知数最后抵消掉，故所设未知数并不影响最后结果，所以我们可以在做题过程中直接进行特值求解，即将成本特值为100或其他方便我们计算的数值，再将售价和利润用特值表示出来进行求解。

有些考生可能会注意到，在进行题目讲解过程中将利润问题中的相关量依靠表格呈现给大家，这样在进行求解时可以更直观的将题干中的信息呈现给我们，同时也更容易得到等量关系。

各位考生可以利用所讲方法将利润问题由难化简，从而赢得更高的分数。

学会这两招，行测数量关系你还放弃吗？

大部分同学可能对数量关系的态度是“放弃”，但是在实际考试中，并不是所有数量关系题目都难，我们要做的就是在有限时间内尽可能的多做一些题。解决问题还是有方法可寻的，接下来政华教育给各位同学介绍两类思路。

整除法

例1：某校二年级全部共3个班的学生排队。每排4人、5人或6人，最后一排都只有2人。这个学校二年级有( )名学生。

A.120 B.122 C.121 D.123

【答案】B【解析】通过题干描述，我们会发现出现了“每”字，那可以考虑到用整除去做，每排4人、5人、6人，最后一排都只有2人。由此我们得出总人数把这两个人去掉应该能既被4整除，又被5整除，还能被6整除，也就是120整除，则二年级有120+2=122名学生。所以选择B项。

赋值法

例2：一项工程，甲单独做10小时可完成，已单独做需要12小时可完成，甲乙两个人同时工作5小时后，甲另有其他的事情去做，只有乙继续工作，那么完成这项工作共用了几个小时( )

A.5 B.6 C.7 D.8

【答案】B【解析】此题的工作总量特值为60，甲的效率为60÷10=6，乙的效率为60÷12=5，甲乙同时工作5小时，完成(6+5)×5=55，还剩60-55=5，乙还需要做5÷5=1小时，所以共需要5+1=6小时。所以选择B。

例3：某市有甲乙丙三个工程队，工作效率比为3：4：5。甲队单独完成A工程需要25天，丙队单独完成B工程需要9天。若三个工程队合作，完成这两项工程共需要多少天( )。

A.6 B.7 C.8 D.10

【答案】D【解析】当题干中给出了完成这项工程的效率比或能推导出效率之间的关系，就把工作效率特值为最简比数值。由此可得，甲的效率特值为3，乙的效率特值为4，丙的效率特值为5，A工作总量为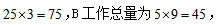所以选择D。

总结

整除特性适用于当题干出现平均、每、倍数、整除或题干有分数、小数、百分数时去使用。赋值法多数用在工程问题和利润问题中。

相信大家通过今天的学习，能够对数量有新的认识！