行测数量关系解题技巧

2022省考行测定位法巧解概率

自公考开始，概率问题一直是公职类考试的热门考点，部分省份在同一套试卷中能出现2-3道题。而近4年，能用定位法解决的概率问题如雨后春笋，出现在各类考试的试题中，经久不衰。今天在这里给大家介绍一下关于数量关系中“定位法”的题型特征与解题思路，帮您既快又准的拿下相关题目，为您行测分数添砖加瓦！

一、“定位法”题型特征。

同一样本中，遇到要同时考虑两个相互制约的元素时，可以使用定位法简化运算。

二、“定位法”解题思路。

将其中的一个元素A先固定，再考虑另一元素B。

注：若先固定的A元素，不论如何选择都不影响B元素选择的概率，则A发生的概率为1，此时，所求=P(元素A)×P(元素B)=P(元素B)。

三、“定位法”在题目中的运用。

例题1：某单位的会议室有5排共40个座位，每排座位数相同。小张、小李随机入座，则他们坐在同一排的概率：（   ）

A.不高于15%

B.高于15%但低于20%

C.正好为20%

D.高于20%

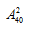【答案】B【解析】方法一：公式法。“某单位的会议室有5排共40个座位，每排座位数相同”即每排8人。“小张、小李随机入座”即小张、小李入座每一个座位的概率是相同的。则他们坐在同一排的概率即符合古典概率的公式：总事件为40个座位中，小张、小李任选2个，方法数为；事件A为小张、小李座位在同一排，方法数为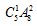。即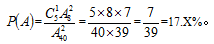方法二：定位法。既然小张、小李随机入座，不妨先让小张选定一个座位，再让小李选。小张先选一个座位的概率为40/40=1，小张选好后，小李只能在剩余的39个座位中随机选，且要想和小张在同一排，小李只能在小张选定的那一排剩余的7个位置中任选，概率为7/39，则满足小张、小李在同一排的概率=1×7/39=17.X%。故答案为B。

例题2：某次圆桌会议共设8个座位，有4个部门参加，每个部门2人，排座位时，要求同一部门的两人相邻，若小李和小王代表不同部门参加会议，则他们座位相邻的概率是：（   ）

A.1/48    B.1/24     C.1/12      D.1/6

【答案】D【解析】假设先让小李随机选择座位，概率是1；根据排座位时，要求同一部门的两人相邻，则小李选完座位之后，他的部门同事只能坐在其旁边的座位上，此时还剩下6个座位，其中只有1个座位能跟小李相邻，则小王选择此座位的概率是1/6。分步用乘法，小李和小王座位相邻的概率为1×1/6=1/6。故答案为D。

以上介绍的“定位法”巧解概率问题，小伙伴们了解并熟练运用以后就能够更加轻松解决数量关系中涉及的相关题目，提高解题的速度与正确率。

行测数量关系行程问题之多次相遇

随着越来越多的人加入到省考大军当中，省考的竞争也变得日益激烈。那么想要取得好成绩就不能忽视考试当中的任何一部分。很多有过备考经验的同学都会认为数量关系是行测问题里一块难啃的硬骨头，但是很多时候硬骨头并不是无法攻克的。今天就带着大家一起了解一下行程问题当中有规律可循的多次相遇问题。我们通过举例的方式带大家研究一下直线异地多次相遇中的直线二次相遇的运动过程。

问题描述

甲、乙两人以均匀的速度分别从相距1200米的A、B两地同时出发，相向而行，到达对方出发点后立即返回、已知甲每分钟走60米，乙每分钟走40米。

画行程图

1.画出从出发到两人第一次相遇的行程图(甲的行进路线用实线表示，乙的行进路线用虚线表示)。

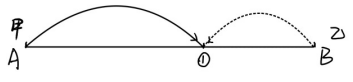
在这一过程和中圈1为甲乙第一次相遇的点，实线为甲走过的路程，虚线为乙走过的路程，那我们观察这个行程图不难发现，甲乙两人所走过的路程和就应该是AB的全程，也就是1200米。那么此时两人所用时间就可以用路程和除以速度和表示，也就是1200÷（60+40）=12，，求得时间之后我们又能得到甲乙分别走过的路程为720米和480米。

2.画出两人第一次相遇到第二次相遇的行程图。

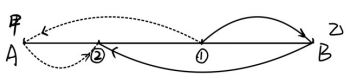
在这一过程中我们用圈2来表示甲乙第二次相遇的点，我们来观察第二张行程图，发现此时甲乙两人走过的路程和变成了两段的AB段路程，也就是2400米，变为了原来的两倍。那么我们可以得到两人所用时间为2400÷（60+40）=24分钟，进而可以得到甲和乙所走过的路程分别为24×60=1440米和24×40=960米。

那么通过观察以上两个表格我们可以得到一个结论，就是从第一次相遇到第二次相遇，两人的路程和、所用时间、甲走过的路程、乙走过的路程为第一次相遇的路程和、所用时间、甲走过的路程、乙走过的路程的2倍。

例题：a大学的小李和b大学的小孙分别从自己学校同时出发，不断往返于a、b两校之间。现已知小李的速度为85米/分钟，小孙的速度为105米/分钟，且经过12分钟后两人第二次相遇。问第一次相遇到第二次相遇两人共走多少米（   ）？

A.2280          B.1960           C.1680           D.1520

【答案】D【解析】设a大学和b大学之间的距离为S米，因为小孙和小李相遇两次，则两人走过的路程总共为3S米，根据题意可得：12×(85+105)=3S，解得S=760，即小孙和小李从开始到第一次相遇共走760米。题干所求第一次到第二次相遇共走的距离，我们可以使用上面推导的结论，所求第一次到第二次相遇共走的距离是2S，即1520米。

希望大家能够通过这个规律在未来的做题当中快速的去解决这种二次相遇的问题！

行测数量关系计算问题之不定方程

行测考试中都会考察数量关系，而数量关系有些题难度又比较大，很多考生具有畏难情绪会选择放弃这部分题目。其实数量关系中有许多题目我们完全有能力得到分数，比如说计算问题。今天给大家介绍数量关系中的不定方程，希望大家能够攻克这一考点。

知识铺垫

当方程中未知数的个数大于独立方程的个数时，我们称这一类的方程叫不定方程，例如：3x+2y=8。

在做题时，找到等量关系并不难，难的是方程的求解。对于不定方程来说，在任意值范围内有无数组解，但是有些方程给它规定范围后解的数量就是有限个甚至是唯一的了。接下来我们就一起看看不定方程的求解。

例题1：3x+4y=101，已知x，y为正整数，则x=(     )。

A.13       B.17           C.19          D.21

【答案】C【解析】所求均在选项中，故将选项直接代入求解，当x=13时，解得y=15.5，不是整数，排除A项；当x=17时，解得y=12.5，不是整数，排除B项；当x=19时，解得y=11，符合题意，C项保留；当x=21时，解得y=9.5，不是整数，排除D项。故答案选C。

例题2：3x+7y=33，已知x、y为正整数，则y=(    )。

A.1       B.3         C.5         D.7

【答案】B【解析】通过观察发现3x、33都能被3整除，故7y也一定能被3整除，但7和3互为质数，则只能是y为被3整除，选项中只有3符合。故答案选B。

例题3：甲、乙、丙三种货物，若购买甲3件，乙7件，丙1件，共需325元；若购买甲4件，乙10件，丙1件，共需410元。那么购甲、乙、丙各1件，共需多少元（   ）？

A.100      B.125           C.135          D.155

【答案】D【解析】根据题意可设每件甲x元，乙y元，丙z元。可列出方程组如下：

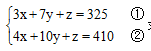
求x+y+z的值。

方法一：把①×3-②×2可得x+y+z=325×3-410×2=155，故答案选D。

方法二：因不定方程在任意值范围为的解有无数组，其中必定有x为0或y为0或z为0的情况，而现在让求x+y+z的值，说明此值必定是个定值，则可令其中一个未知数为0；为使接下来的方程容易求解，可令未知数前的系数复杂的未知数为0，故此题可令y=0，可得3x+z=325、4x+z=410，两式相减可得x=85，代入可得z=70。则x+y+z=85+0+70=155。故答案选D

通过以上例题的展示，希望可以给各位考生在不定方程求解中提供思路。在接下来考试中遇到类似的计算问题，希望各位考生都能拿到分数。

行测数字推理常考的组合数列有哪些

数字推理是行测数量关系中的常考题型，其中等差数列、等比数列、和数列作为常考数列广大考生都比较熟悉，而组合数列同样作为高频考点，考生们往往无从下手。在此向各位考生介绍组合数列常见的考查规律有哪些。

组合数列考察之一：间隔数列。

例1：1，2，7，13，49，24，343，(   )

A.35         B.69          C.114          D.238

【答案】A【解析】间隔组合数列，奇数项1、7、49、343是公比为7的等比数列，偶数项2、13、24、(35)是公差为11的等差数列。

通过这道题目我们会发现组合数列一般数列较长，且非单调。像这种奇数项和偶数项均满足某种规律的间隔数列是组合数列的常考考点之一。

组合数列考察之二：分段数列。

例1：0，-1，1，-4，0，-5，9，(   )

A.-1       B.-16         C.-7           D.-8

【答案】B【解析】分段组合数列。每两个数字一组，二者之和依次为-1，-3，-5，(-7)，是公差为-2的等差数列，应填入-7-9=(-16)。

例2：4，5，15，6，7，35，8，9，(    )

A.27       B.15         C.72          D.63

【答案】D【解析】分段数列，每三个一组，4×5-5=15、6×7-7=35、8×9-9=(63)。

以上两道题考查的都是分段数列，分段数列是将数列进行合理的分组，将每一组作为一个整体，整体之间或整体内部满足某种规律。一般情况两两分段以八项居多，三三分段以九项居多。

组合数列考察之三：数位组合。

例1：22，44，86，(          )，3210，6412

A.108          B.168        C.78        D.118

【答案】B【解析】将每个数字分为前后两部分来看，前一部分2，4，8，(16)，32，64是公比为2的等比数列；后一部分2，4，6，(8)，10，12是公差为2的等差数列，所填应为(168)。

例2：448，516，639，347，178，(        )

A.163        B.134         C.785          D.896

【答案】B【解析】每项百位、十位数字的和等于个位数字。

通过以上题目可以发现若大部分数字都是多位数(≥3位)，可考虑数位拆分找规律。

我们通过上面的内容给大家展示了间隔数列、分段数列、数位组合数列的特征及常见考查形式，组合数列的数列长度一般较长(项数≥7)，数字变化幅度不大且一般不具有单调性。优先考虑间隔分组，再考虑两两分段或三三分段。数位组合数列中的各项一般由多位数(≥3位)组成，数位组合数列通常将多位数拆成多个部分找规律。相信通过上面的讲解，大家对于组合数列已经胸有成竹，另外数字推理可能会存在不常见的考点，考试中希望大家保持良好的心态，平时需要多做题，多积累。