行测数量关系解题技巧
遇到容斥问题不要慌，找寻规律最重要
在行测数量关系的考试中，容斥问题因为其题干特征的特殊性，都会成为考生考试时首选解题的题型。但其考察形式多变，需要考生深入理解和掌握容斥问题的解题公式就显得尤为重要。
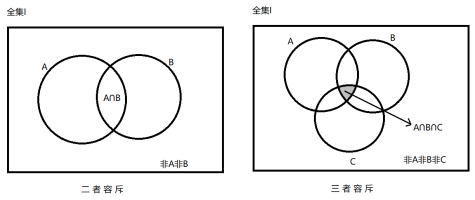
容斥问题的基本公式为
二者容斥公式：全集I=A+B-A∩B+非A非B
三者容斥公式：全集I=A+B+C-A∩B-B∩C-A∩C+A∩B∩C+非A非B非C
【例题1】某医院门诊统计某天挂号的病人，内科150人，外科90人，内外科都求诊的有20人，这天至少有多少病人？（ ）
A.240 B.220 C.200 D.170
【答案】B【解析】根据题干所述，题目为容斥问题，所求为全集，可列式，150+90-20=220人。故本题选B。
【例题2】40人参加计算机等级考试，只有理论和上机考试均及格方为通过。在理论考试中有34人及格，上机考试中有32人及格，两次考试中都没有及格的有4人。通过计算机考试的有多少人？（ ）
A.30 B.60 C.80 D.100
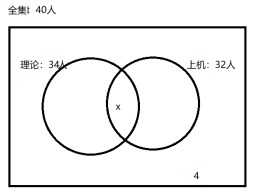
【答案】A【解析】根据题干信息，可分析题干整理如下图所示。设通过计算机考试的有x人。可列式，40=34+32-x+4，解得x=30。故本题选A。
【例题3】18名游泳运动员中，有8名参加仰泳，有10名参加蛙泳，有12名参加自由泳，有4名既参加仰泳又参加蛙泳，有6名既参加蛙泳又参加自由泳，又5名既参加仰泳又参加自由泳，有2名这三个项目都参加。三个项目都没有参加的有多少名？（ ）
A.1 B.2 C.3 D.4
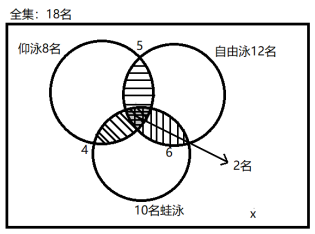
【答案】A【解析】根据题干信息，可整理题干信息如下图所示。设三个项目都没有参加的有x名，可列式：8+10+12-4-6-5+2+x=18，解得x=1。故本题选A。
容斥问题需要考生们勤加练习，找到列式规律，在解题时可利用尾数的方法确定答案。
掌握最不利原则
在行测考试中，经常能够遇到有一种很有趣的题型：最不利原则。这种题目相对来说比较简单，是考试中我们不容错过的类型，接下来就带领大家了解最不利原则这个题型。
【例题】在一个箱子中有7个红球和6个白球。
问题一：至少从中拿出多少个数才能够拿到红球？
【答案】1个【解析】题目问拿到红球的最小值，最幸运的情况就是只拿一个就拿到红球。
问题二：至少从中拿出多少个球才能保证拿出红球？
【答案】8个【解析】题目问保证拿出红球，此时只有拿出全部的白球7个在这个基础上再拿多一个，那多拿的一个一定是红球，即拿到8个才能一定能保证拿到红球。拿出全部的白球可以理解为最不利的情况，所以这种题的解题思路即找出最不利的情况数再加一。
通过上题我们就可以了解最不利原则的思路：
一、题型特征：题干出现“至少……才能保证……”的字样我们就考虑最不利原则。
二、解题方法：最不利情况数+1。
【例题1】有300名求职者参加高端人才专场招聘会，其中软件设计类、市场营销类、财务管理类和人力资源管理类分别有100、80、70和50人。问至少有多少人找到工作，才能保证一定有70名找到工作的人专业相同？（ ）
A.258 B.195 C.188 D.257
【答案】A【解析】题目问的是“至少......才能保证......”，对于这一类题目，一般需要考虑最不利原择。此题的最不利情况为4个专业每个专业都录取了69人。但是通过题目发现软件设计类、市场营销类、财务管理类可以满足每个专业录取69人，但是人力资源管理只有50人，但是我们考虑最不利情况则50人全部录取。此时任意再录取1人能够保证有70名找到工作的人专业相同。因此至少要69×3+50+1=258人找到工作才可以，故本题选A。
【例题2】某区要从10位候选人中投票选举人大代表，现规定每位选举人必须从这10位中任选两位投票，问至少要有多少位选举人参加投票，才能保证有不少于10位选举人投了相同两位候选人的票？（ ）
A.382位 B.406位 C.451位 D.516位
【答案】B【解析】先思考共有多少种投票方式，是在10个人中选择两人有多少种选法，利用排列组合：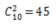
种投票方式。问不少于10位选举人投了相同两位候选人的票，考虑最不利情况，为每种投票方式都有9个人投票，此时再多一个人投票，不算此人投票情况如何，必定有10人的投票情况相同。所以共9×45+1=406人。
定位法速解古典型概率问题
在行测备考当中，古典型概率问题一直是非常重要的一部分，在考试中几乎每年都有出现。但是由于其经常和排列组合问题相结合，相对灵活，所以就成为了大家备考中的一大难点。今天教大家一种新的方法——定位法来速解古典型概率。
【方法介绍】
古典型概率研究的是有限个等可能事件发生的概率，求解公式为P(A)=A事件所包含的等可能样本数/总的等可能样本数。在解该种概率题目时，当遇到要同时考虑相互联系的元素时，可以先将其中一个固定，再考虑其他元素的所有可能情况，从而进行求解。
【例题1】从3双完全相同的鞋中，随机抽取一双鞋的概率是：（ ）
【答案】D【解析】由于要抽取出一双鞋，所以元素之间存在联系故可用该方法。若一只鞋已经选定之后，在剩下的5只鞋中只有3只能与之凑成一双，因此随机抽取一双鞋的概率是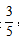
，故本题选D。
【例题2】某单位的会议室有5排共40个座位，每排座位数相同。小张和小李随机入座，则他们坐在同一排的概率：（ ）
A.不高于15% B.高于15%但低于20% C.正好为20% D.高于20%
【答案】B【解析】由于小张和小李要坐在同一排有联系故可用该方法。若小张固定了座位，剩下39个座位小李可以选，小李要和小张坐在同一排，只能在小张坐的那一排剩余的7个位置上选，故两人坐在同一排的概率都是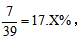
故本题选B。
【例题3】某次圆桌会议共设8个座位，有4个部门参加，每个部门2人，排座位时，要求同一部门的两人相邻，若小李和小王代表不同部门参加会议，则他们座位相邻的概率是：（ ）
【答案】D【解析】由于小李和小王要相邻有联系故可采用该方法。若先固定小李的座位，根据排座位时，要求同一部门的两人相邻，则小李选完座位之后，他的部门同事只能坐在其旁边的座位上，此时还剩下6个座位，其中只有1个座位能跟小李相邻，则小王选择此座位的概率是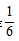
，故本题选D。
以上就是关于定位法求解古典型概率问题的介绍，相信通过三道例题的详细分析各位小伙伴已经非常清晰地认识定位法的含义和应用环境了。那么大家在以后的练习中就快快实践起来吧！
排列组合之“插空法”
黑板上的排列组合除了会让我们想起那些年我们一起追过的女孩，更多的是它的变化多端。虽然在茫茫题海中一眼就能认出它，但它就像女孩子的心思一样让人摸不着头脑。今天为大家讲解的是排列组合中常见的一种方法，让大家能够“有法可依”。
下面先来看一道题目：
【例题1】由数字1、2、3、4、5、6、7组成无重复数字的七位数，求三个偶数互不相邻的七位数的个数。（ ）
A.600 B.720 C.1440 D.2880
【答案】C【解析】因为三个偶数2、4、6互不相邻，所以考虑偶数之间需要穿插奇数，但穿插多少个奇数呢？我们发现穿插个数的不同会导致分很多类，求解起来会比较复杂。不妨换个思路，先将1、3、5、7四个奇数排好，有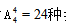
排法，再将2、4、6分别“插入”到第一步排的四个数字的五个“间隙”(包括两端的两个位置)中的三个位置上，有
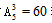种排法，根据乘法原理共有24×60=1440种不同的排法，所以共有1440个符合条件的七位数。故本题选C。
当题目中出现关键信息“不相邻”即可考虑“插空法”。解题步骤如下：
(1)先安排不相邻的元素之外的其他元素；
(2)将不相邻的元素插在其他元素形成的空中。
【例题2】某展室有9个展台，现有3件展品需要展出，要求每件展品独自占用1个展台，并且3个展品所选用的展台既不在两端又不相邻，则不同的展出方法有多少种？（ ）
A.10 B.20 C.60 D.80
【答案】C【解析】因为3个展品互不相邻，先排其他6个空展台，由于空展台是相同的，所以调换顺序无区别。再将3个有展品的展台插入到空展台之间的空位中，由于展品不能在两端，所以只有5个空位可选，有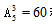
种排法。故本题选C。
注意：两端是否可以看作空位要根据题目要求进行判定。
【例题3】把12棵同样的松树和6棵同样的柏树种植在道路两侧，每侧种植9棵，要求每侧的柏树数量相等且不相邻，且道路起点和终点处两侧种植的都必须是松树。问有多少种不同的种植方法？（ ）
A.36 B.50 C.100 D.400
【答案】C【解析】根据题意可知每侧道路种植9棵树，其中包括3棵柏树和6棵松树，由条件可知要求起点和终点需种植松树，且柏树不相邻，故需在6棵松树中间的5个空中种植3棵柏树，有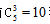
种，两侧均种植，故有10×10=100种种植方法。故本题选C。
相信通过多加练习，大家能够在考场上轻松解决此类问题。
