政华教育

【例题】在一条公路上每隔10公里有一个仓库，共有5个仓库，一号仓库存有10吨货物，二号仓库存有30吨货物，三号仓库存有20吨货物，五号仓库存有15吨货物，四号仓库是空的。现在要把所有的货物集中存放在一个仓库里，如果每吨货物运输1公里需要0.5元运输费，则集中放在哪个仓库中运输总费用最低？（）

A.一号 B.二号 C.三号 D.五号

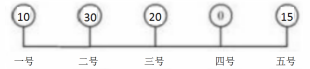
【答案】B【解析】在这道题目当中，可以将选项涉及到的4种情况分别计算出来，并进行比较得出。

如果集中到一号仓库，运输总费用为：30×10×0.5+20×20×0.5+15×40×0.5=650元；

如果集中到二号仓库，运输总费用为：10×10×0.5+20×10×0.5+15×30×0.5=375元；

如果集中到三号仓库，运输总费用为：10×20×0.5+30×10×0.5+15×20×0.5=400元；

如果集中到五号仓库，运输总费用为：10×40×0.5+30×30×0.5+20×20×0.5=850元。

经过比较可知，集中到二号仓库，运输总费用最低。

这道题目也可以利用“支点法”进行判断：在任意两个仓库之间确定一点，记为支点，计算支点两侧货物的累计重量，由轻的一端向重的一端集中，不用考虑距离和单位距离运费。根据上述方法，如果将支点确定一号仓库与二号仓库之间，那么左侧的累计重量为10，右侧的累计重量为30+20+15=65，左侧比右侧轻，因此向移动；如果将支点确定二号仓库与三号仓库之间，那么左侧的累计重量为10+30=40，右侧的累计重量为20+15=35，右侧比左侧轻，因此向移动左侧。因此，可以确定为二号仓库，故本题选B。

通过上面这道题的分析大家不难发现，只要是在直线上分布若干仓库，要把所有的货物集中存放在一个仓库里，并且要使运输总费用最低，都可以利用支点法进行判断，并且在判断时只需考虑支点两侧累计重量的大小，由轻向重移动，而不需要考虑其他因素，会使得判断过程更加简洁，计算量较小。

“公式法”快速解答行测利润的相关问题

利润问题是行测数量关系考题中常见的一种题型。这类题型往往难度不大，但多数考生对于利润问题往往只能够使用最基本的方程法来进行解答，倘若时间比较紧张便会放弃这一类题目。其实许多利润问题是可以通过一些基本的公式来快速解答的，下面一起来探索一下这把快速解题的钥匙。

一、对基本公式“利润=售价-成本”的应用

【例题】某商品按照定价出售，每个可获利60元。按定价打八折出售10个所获得的利润，与按定价每个减价30元出售15个所获得的利润相同。该商品的定价为多少元？（）

A.75 B.80 C.85 D.90

【答案】A【解析】根据利润问题中的基本公式“利润=售价-成本”，当成本不变时，我们发现售价降低多少，利润也会降低多少。因此，当售价降低30元，利润也会降低30元，变为60-30=30元/个。售出15个，共计获利15×30=450元。由题可知，打八折售出10个所获利润也为450元，因此，打八折售出一个的利润为450÷10=45元/个。与原来相比，单个的利润由60元降为45元，下降了15元，所以，售价也应下降15元。具体来看，售价由原售价变为了原售价的0.8倍，所以售价下降了原售价的0.2倍。即：0.2×原售价=15，解得，原售价为15÷0.2=75元。

二、对基本公式“总利润=单利×销售量”的应用

【例题】某新款手机上市时的单价是2598元，销售一段时间后，厂家采取降价促销的策略，手机单价直降300元，于是每月的销量提升为原来的2倍，每月利润提升为原来的1.5倍，则该款手机的成本价是( )元。

A.1698 B.1598 C.1498 D.1398

【答案】D【解析】根据利润问题中的基本公式“总利润=单利润×销售量”，从题目中我们看到销售量变成了原来的2倍，而总利润只变为原来的1.5倍，说明，单利变成了原来的0.75倍。具体来看，售价下降了300元，因此单利也下降的300元；而单利由原来的单利变为原单利的0.75倍，下降了原单利的0.25倍。因此0.25×原单利润=300，解得原单利润为300÷0.25=1200元，进而可以得到成本应等于原售价2598元减去原单利1200元，即1398元。

通过以上几道题目的展示，相信考生对利润问题的解题思路有了一些新的认识，在此之上考生可以多加练习，以便更好地掌握它，并在考场上发挥这种方法的作用。

啃下行测数量关系这块“硬骨头”

首先我们在心态上要摆正，不要去恐惧数学。事实上大多数的数量关系题目，是根据我们小初高的题目变来的。千万不要害怕，不可能所有题目都非常的难，大多数题目只是“巧”而已，只要肯学，至少是能攻克几个题目的。接下来谈谈学习方法。在这里我们可以分三个阶段进行：

第一阶段：搞懂题目怎么做

所谓的搞懂，不是去记公式，而是自己去推导解题的过程。比如工程问题，自己去推导工作效率比会让我得到什么结果，工作总量又如何设合适等等。其实很多题目，可以用列方程的方法解决，但是很多同学觉得列方程很LOW，但是方程在数量关系问题当中实在是太重要了，一定要强化好。诸如此类的基础理论一定要学扎实，一定要砸瓷实。这个过程可以称之为打基础，大约需要十到十五天的时间。

第二阶段：整理解题方法

在初步掌握了方法之后，再对各类题型进行适当地分类可以让自己的思路更加清晰。比如工程类问题、行程问题等。分类之后可以寻找两大类之间的相同之处，比如上述两个问题就有“时间=总量/效率”，把路程看为工作总量，速度看为工作效率，同样适用该公式。总之需要大家对理论的理解要特别深入，多举一反三，多思考，这个阶段大概需要五到十天。

第三阶段：大量刷题练习

练习又可以分为两个小阶段，第一个阶段是分类练习，第二个阶段是综合练习。分类练习就是针对各种类型的题目反复练习，巩固自己擅长的，弥补自己不足的，大约会用掉十天到十五天；第二个阶段综合练习，可以每天随机选取一套试卷练十个题，不要多练，十个题，不论做对做错，都要进行多角度解析，清空思维误区。这个过程可以一直持续到考试前三天。

总体而言，数量关系不是一个啃不动的硬骨头，大家要静下心，一步步来，相信最终都会有所突破！

多者合作不担忧设立特值解千愁

工程中的多者合作问题在行测考试中屡见不鲜，但考生往往由于时间紧张或者题目材料过长(一般超过三行)，从而对该类题目选择放弃，导致失分。但该类题目一旦理清思路，求解过程会很轻松。所以对于此类问题要尽可能地去做。特值法可以很好的为大家提供解题思路，在后续的解题过程中不迷茫。

工程问题涉及的公式：工作总量=工作效率×工作时间，即W=Pt

特值法的应用

一、题目中出现多个完成工作的时间，将工作总量设为特值，特值设为时间的最小公倍数；

二、题目中出现或者利用已知条件可求多者效率之比，将效率设为特值，效率之比为多少，特值设为多少。

以上为设特值的两种情况，下面通过题目展示其具体应用。

【例题1】某项工程，甲工程队单独施工需要30天完成，乙工程队单独施工需要25天完成。甲队单独施工了4天后，改由两队一起施工，期间甲队休息了若干天，最后整个工程共耗时19天完成，问甲队中途休息了几天？（）

A.1 B.3 C.5 D.7

【答案】D【解析】题目中出现“甲工程队单独施工需要30天完成，乙工程队单独施工需要25天完成”，有两个完成工作的时间，将工作总量W设特值，设为30、25的最小公倍数150，可以求得甲的效率为5，乙的效率为6。题目中描述，“甲队单独施工了4天，最后整个工程共耗时19天”，可以推出乙工作了19-4=15天，那么乙完成的工作量为6×15=90，则甲完成的工作量为150-90=60，完成以上工作量甲需工作60÷5=12天，已知整个工程共耗时19天，则甲休息了19-12=7天。故本题选D。

【例题2】手工制作一批元宵节花灯，甲、乙、丙三位师傅单独做，分别需要40小时、48小时、60小时完成。如果三位师傅共同制作4小时后，剩余任务由乙、丙一起完成，则乙在整个花灯制作过程中所投入的时间是：（）

A.24小时 B.25小时 C.26小时 D.28小时

【答案】A【解析】题目中出现“单独做，分别需要40小时、48小时、60小时完成”，有三个完成工作的时间，将工作总量W设特值，设为40、48、60的最小公倍数240，可以求得三位师傅的效率，甲的效率为6，乙的效率为5，丙的效率为4，“三位师傅共同制作4小时”完成的工作量为(6+5+4)×4=60，剩余任务由乙、丙一起完成，还需(240-60)÷(5+4)=20个小时，则整个过程需要投入4+20=24个小时。故本题选A。

【例题3】一项工程由甲、乙、丙三个工程队共同完成需要22天，甲队工作效率是乙队的二分之三倍，乙队3天的工作量是丙队2天工作量的三分之二。三队同时开工，2 天后，丙队被调往另一工地，那么甲、乙再干多少天才能完成该工程？（）

A.20 B.28 C.38 D.42

【答案】C【解析】题目中出现“甲队工作效率是乙队的二分之三倍，乙队3天的工作量是丙队2天工作量的三分之二”，由此可以得到甲乙的效率之比为3：2，乙丙的效率之比为4：9，则甲乙丙三者的效率之比为6：4：9，则可以假设甲的效率为6，乙的效率为4，丙的效率为9，那么工作总量W=(6+4+9)×22=418，“三队同时开工2天”完成的工作量为(6+4+9)×2=38，剩下的工作量为418-38=380，还需甲乙工作380÷(6+4)=38天。故本题选C。

通过以上三道题目的分析，想必大家对于多者合作的问题已经有所了解，可以多做一做相关的问题，熟能生巧。

整除法巧解计算问题

数量关系是行测考试中令许多考生感到头疼的部分，它的考查方式灵活、难度相对较高，而考场上答题时间紧张，所以数量关系题目经常被考生舍弃。考生要想在时间紧题量大的数量关系中拿到高分，就必须在备考阶段熟练掌握一些特定题型的解题技巧。在众多技巧中整除作为一种题型特征明显、计算思路简单的解题技巧，广大考生在备考时一定要确保能灵活运用。

一般题干中文字表述有“倍”、“每”、“平均”、“整除”或数据中出现小数、分数、百分数、比例时，考生可以结合题干中的计算关系和选项设置判断能否使用整除法。下面我们就结合典型例题详细给大家介绍一下整除的应用环境和方法。

【例题1】苗苗有一堆草莓，乐乐也有一堆草莓。苗苗的草莓五个五个地数，最后剩两个，七个七个地数，最后还是剩两个；乐乐的草莓五个五个地数，最后剩四个，六个六个地数，最后剩三个。已知苗苗比乐乐多8个草莓，则苗苗的草莓数为( )。

A.87 B.92 C.102 D.107

【答案】D【解析】由题意可知，苗苗的草莓数减去2是既是5的倍数又是7的倍数，即苗苗的草莓数减2是35的倍数，只有D项符合，故本题选D。

总结：整除法是一种排除错误选项的方法，当发现所求数据具有整除特性，可根据这一特点迅速选出正确选项。

【例题2】幼儿园的老师将122颗糖分发给全班的小朋友，分发完后发现有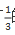的小朋友有两颗糖，有3个小朋友有3颗糖，其他的小朋友都只有1颗糖。问全班共有多少个小朋友？（）

A.57 B.73 C.87 D.92

【答案】C【解析】由“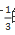的小朋友有两颗糖”，可知全班小朋友的人数是3的倍数，排除B、D。代入A项，若全班共有57个小朋友，则小朋友中有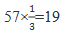人分到了两颗糖，57-19-3=35人分到1颗糖，共需要19×2+3×3+35=82颗糖，与122颗矛盾，排除A项。故本题选C。

总结：根据整除特性判断选项时若只能排除部分错误选项，剩余选项则需要代入验证确定正确答案。

【例题3】高校某专业70多名毕业生中，有96%在毕业后去西部省区支援国家建设，其中去偏远中学支教的毕业生占该专业毕业生总数的20%，比任职大学生村官的毕业生少2人，比在西部地区参军入伍的毕业生多1人，其余的毕业生选择去国有企业西部边远岗位工作。问去国有企业西部边远岗位工作的毕业生有多少人？（）

A.23 B.26 C.29 D.32

【答案】B【解析】由题干可知，“70多名毕业生”说明毕业生人数为71~79的某个整数。“有96%在毕业后去西部省区支援国家建设”，96%化简成最简分数是24/25，说明西部支援人数占毕业生人数的24/25，可知毕业生人数是25的倍数，即75人，则毕业后去西部支援国家建设的有96%×75=72人，其中去中学支教、任职村官、参军入伍的分别有20%×75=15人、15+2=17人、15-1=14人，所以去国有企业西部边远岗位工作的毕业生有72-15-17-14=26人。故本题选B。

总结：整除特性除了可排除错误选项外，有时还可将题干中的未知条件转化为已知条件。题干条件中若存在已知取值范围的未知整数条件(如例3中“70多名毕业生”)，可先根据题干中能体现整除特性的数据(小数、分数、百分数、比例)确定该未知整数符合取值范围的具体值，再以此为已知条件求解问题。

综上所述，考生可以抓住整除的题型特征多加练习，养成善于发现整除关系思维习惯，提高自己的答题速度。