
行测数量关系解题方法
数学运算之方阵问题的求解
方阵问题是数学运算中的一类常考题型,一些考生第一次碰到方阵问题的时候不会求解,为了帮助大家能够快速地解决方阵问题,下面就来讲一讲方阵问题。
方阵问题可分为实心方阵和空心方阵,其实空心方阵可以理解为一个大的实心方阵中减去一个小的实心方阵,所以如果会解决实心方阵问题,那么空心方阵问题自然也能会解决。
先来了解一些实心方阵的常用公式。
一个人数为n×n的实心方阵:
1.方阵总人数=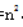 。
。
2.方阵最外层人数=4n-4。
3.方阵相邻层人数相差8(特殊情况:最里面一层人数为1时,与相邻层相差7,其他情况相邻层人数均相差8)。
【例题1】某次运动会需组织长宽相等的方阵。组织方安排了一个鲜花方阵和一个彩旗方阵,两个方阵分别入场完毕后又合成一个方阵,鲜花方阵的人恰好组成新方阵的最外圈。已知彩旗方阵比鲜花方阵多28人,则新方阵的总人数为( )。
A.100 B.144 C.196 D.256
【答案】A【解析】设彩旗方阵为n×n,则总人数为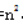 、最外层人数4n-4,由于鲜花方阵的人恰好组成新方阵的最外圈,则鲜花方阵总人数为4n-4+8=4n+4,根据彩旗方阵比鲜花方阵多28人可得:
、最外层人数4n-4,由于鲜花方阵的人恰好组成新方阵的最外圈,则鲜花方阵总人数为4n-4+8=4n+4,根据彩旗方阵比鲜花方阵多28人可得: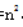 -(4n+4)=28,解得n=8或n=-4(不符合实际),所以n=8,彩旗方阵总人数64,鲜花方阵总人数64-28=36,新方阵的总人数为64+36=100,故本题选A。
-(4n+4)=28,解得n=8或n=-4(不符合实际),所以n=8,彩旗方阵总人数64,鲜花方阵总人数64-28=36,新方阵的总人数为64+36=100,故本题选A。
【例题2】有一列士兵排成若干层的中空方阵,外层共有68人,中间一层共有44人,则该方阵士兵的总人数是( )。
A.296 B.308 C.324 D.348
【答案】B【解析】题干描述为一个中空方阵,最外层有68,中间一层44,根据相邻层人数相差8,68-44=24,所以最外层与中间层相差三层,也就是如果最外层是第一层,往里面数中间层是第四层,所以这个中空方阵一共有七层,且每一层人数构成公差为8的等差数列,中空方阵总人数为44×7=308,故本题选B。
不定方程
数量关系是行测中的必考题型,难度相对较大。通常情况,拿到题目大家都习惯使用方程法进行分析,方程法也确实是我们数量关系部分的重要方法。但有时候,方程可以列出来,但未知量的个数却大于独立方程的个数,没有相应的解题思路。那你可能是遇到了方程中的一类特殊类型——不定方程。那我们应该如何快速解决这一问题呢?
首先我们需要知道什么是不定方程。不定方程是指方程的未知量的个数多于独立方程的个数,分为两种情况:在正整数范围内求解;在任意数范围内求解。接下来我们通过几道例题进行阐述。
【例题1】办公室人员使用红、蓝两种颜色的文件袋装29份相同的文件。每个红色文件袋可装7份文件,每个蓝色文件袋可装4份文件。要使每个文件袋都恰好装满,需要红色、蓝色文件袋分别为几个?( )
A.1、6 B.2、4 C.4、1 D.3、2
【答案】D【解析】假设红色文件袋x个,蓝色文件袋y个,使每个文件袋都恰好装满可得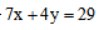 。代入A、B、C选项都不符合,故选择D选项。另解:因x、y只能为正整数,所以4y必为偶数,又因29为奇数,要使等式成立,7x必为奇数,即x为奇数,只有A、D符合。代入A选项,y不是整数,不符合题意,故本题选D。
。代入A、B、C选项都不符合,故选择D选项。另解:因x、y只能为正整数,所以4y必为偶数,又因29为奇数,要使等式成立,7x必为奇数,即x为奇数,只有A、D符合。代入A选项,y不是整数,不符合题意,故本题选D。
因数量关系都是单选题,在没有其它思路的情况下,最快的解题方法就是直接结合选项进行代入求解。但部分题目通过代入较为麻烦,我们还可以用奇偶性进行解题:奇数+奇数=偶数,偶数+偶数=偶数,奇数+偶数=奇数,利用此性质进行求解。
【例题2】小张的孩子出生的月份乘以29,出生的日期乘以24,所得的两个乘积加起来刚好等于900。问孩子出生在哪一个季度?( )
A.第一季度 B.第二季度 C.第三季度 D.第四季度
【答案】D【解析】假设孩子出生月份为x,月份为y,易得29x+24y=900,得到x的值即可得知为第几季度。一年有12个月,需要代入12次,显然不大可取。故需要转换思路,此题可以从数字特性上入手:29为质数,只有1和29两个因数,和900没有非1公因数;24和900有公因数12,即24能被12整除,900也能被12整除,要使等式成立,29x也得能被12整除,x在1-12这个正整数范围内,只能取x=12。故本题选D。
“例题2”这道不定方程题目有真实的生活背景,月份,日期只能取整数,即在正整数范围内求解不定方程。用的是数字的整除特性,整除特性是用的较多的一种解决不定方程的数字特性。尾数法也能解决一些不定方程:某一未知量系数为5的倍数时,它的尾数只能为5或0,利用此特性来解决相应的不定方程。
除了在正整数范围内求解不定方程,还有第二类题型:在任意数范围内求解不定方程。
【例题3】现有甲、乙、丙三种商品,若购买甲1件、乙3件、丙7件共需200元;若购买甲2件、乙5件、丙11件共需350元。则购买甲、乙、丙各1件共需多少元。( )
A.50 B.100 C.150 D.200
【答案】B【解析】设甲、乙、丙的单价分别为x、y、z,易得 本题所求为x+y+z的和,观察选项可知x+y+z为一个定值,即无论其中某个未知数如何取值,其他两个未知数都有相对应的解使x+y+z的和为此定值。观察列式发现z的系数最大,不妨让z=0,此时可得
本题所求为x+y+z的和,观察选项可知x+y+z为一个定值,即无论其中某个未知数如何取值,其他两个未知数都有相对应的解使x+y+z的和为此定值。观察列式发现z的系数最大,不妨让z=0,此时可得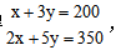 解得x=50,y=50,即x+y+z=50+50+0=100,故本题选B。
解得x=50,y=50,即x+y+z=50+50+0=100,故本题选B。
“例题3”所求的x+y+z的和为一个定值,且对x、y、z并未有正整数的约束,属于在任意数范围内求解不定方程。解决此类问题一般让未知数系数最大的未知数为0,特值进行求解。
关注性价比高
在行测考试中,数量关系一直是难度相对较大的部分。在数量关系中有没有一些思路比较固定,用较少的时间复习,却能有较大的收获题目呢?那么下面给大家介绍几种题型。
【排列组合之隔板模型】
(1)含义
相同元素的不同分堆:把n个相同元素分给m个不同的对象,每个对象至少1个元素,问有多少种不同分法的问题,可以采用“隔板法”。
(2)公式
方法数: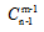 。
。
(3)条件
这类问题模型适用前提相当严格,必须同时满足以下3个条件:
①所要分的元素必须完全相同。
②所要分的元素必须分完,不允许有剩余。
③每个对象至少分到1个,不允许出现分不到元素的对象。
简单应用:题干满足隔板模型的所有条件。
【例题1】有10个相同的篮球,分给7个不同的班,每班至少一个,有多少种分配方案?( )
A.36 B.64 C.84 D.210
【答案】C【解析】此题满足隔板模型的所有条件,直接套用公式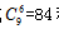 种分配方案。
种分配方案。
【古典概率之定位法解题】
含义:当遇到要同时考虑相互联系的元素时,可以先将其中一个固定,再考虑其他元素的所有可能情况,从而进行求解。
【例题2】一张纸上画了5排共30个格子,每排格子数相同,小王将1个红色和1个绿色棋子随机放入任意一个格子(2个棋子不在同一格子),则2个棋子在同一排的概率:( )
A.不高于15% B.15%~20% C.20% D.20%以上
【答案】B【解析】方法一,5排共有30个格子,每排格子数相同,则每排30÷5=6个格子。总事件是从30个格子中选取2个格子分别放入两个颜色不同的棋子,样本数为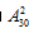 ,所求事件是2个棋子在同一排,则可以先选择1排,再从这一排的6个格子中选取2个格子分别放入两个颜色不同的棋子,分步相乘,样本数为
,所求事件是2个棋子在同一排,则可以先选择1排,再从这一排的6个格子中选取2个格子分别放入两个颜色不同的棋子,分步相乘,样本数为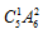 。故所求概率为
。故所求概率为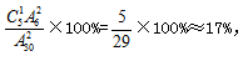 故本题选B。
故本题选B。
方法二,5排共有30个格子,每排格子数相同,则每排有30÷5=6个格子。先从30个格子中任选1个安排红色棋子,此时还剩下29个空格子。若想2个棋子在同一排,则绿色棋子只能挑选红色棋子所在排剩余5个格子中的一个,故2个棋子在同一排的概率为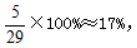 故本题选B。
故本题选B。
【行程问题之牛吃草模型】
含义:同一草场问题是在同一个草场上的不同牛数的几种不同吃法,其中原有草量、每头牛每天吃草量和草每天的生长数量,三个量是不变的。这种题型相对较为简单,直接套用牛吃草问题公式即可进行解答。
(1)追及:一个量使原有草量变大,一个量使原有草量变小
原有草量=(牛每天吃掉的草-每天生长的草)×天数
【例题3】牧场上一片青草,每天牧草都匀速生长。这片牧草可供10头牛吃20天,或者可供15头牛吃10天。问:可供25头牛吃几天?
【答案】5【解析】牛在吃草,草在匀速生长,所以是牛吃草问题中的追及问题,原有草量=(牛每天吃掉的草-每天生长的草)×天数,设每头牛每天吃的草量为“1”,每天生长的草量为X,可供25头牛吃T天,所以(10-X)×20=(15-X)×10=(25-X)×T,先求出X=5,再求得T=5。
(2)相遇:两个量都使原有草量变小
原有草量=(牛每天吃掉的草+其他原因每天减少的草量)×天数
【例题4】由于天气逐渐冷起来,牧场上的草不仅不长大,反而以固定的速度在减少。已知某块草地上的草可供20头牛吃5天,或可供15头牛吃6天。照此计算,可供多少头牛吃10天?( )
【答案】5【解析】牛在吃草,草在匀速减少,所以是牛吃草问题中的相遇问题,原有草量=(牛每天吃掉的草+每天减少的草)×天数,设每头牛每天吃的草量为“1”,每天减少的草量为X,可供Y头牛吃10天,所以(20+X)×5=(15+X)×6=(Y+X)×10,先求出X=10,再求得Y=5。
排列组合中的“三种方法”
“黑板上的排列组合你舍得解开吗……”一听到这句歌词很多同学都在想,这是我舍不舍得的问题吗?这是我会不会的问题啊!那么对于排列组合而言真的那么难吗?作为数量关系板块中的高频考点,我们真的束手无策吗?从最近几年的试题来看,这部分的难度确有上升的趋势,而且题型也越来越灵活,所以我们带大家一起来学习排列组合中的三种小方法。
排列组合的核心:统计方法数
【例题1】甲、乙、丙、丁、戊五个人排成一列,其中甲不站在头或尾的位置,共有多少种不同的排列方法?( )
A.24 B.36 C.72 D.96
【答案】C【解析】甲是这5个人里面有限制条件的元素,所以就优先考虑甲。让他站在除头尾以外的中间的3个位置,有3种选择;然后安排除甲以外的另外4个人,有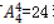 种方法。所以最终共有3×24=72种方法,故本题选C。
种方法。所以最终共有3×24=72种方法,故本题选C。
小结:优限法:对于有限制条件的元素(或位置)的排列组合问题,在解题时优先考虑这些元素(或位置),再去解决其它元素(或位置)。
【例题2】由数字1、2、3、4、5、6、7组成无重复数字的七位数,求三个偶数必相邻的七位的个数:( )
A.459 B.720 C.920 D.4590
【答案】B【解析】因为三个偶数2、4、6必须相邻,所以先将2、4、6三个数宇“捆绑”在一起有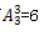 种不同的“排列”方法,再将捆绑后的元素与1、3、5、7进行全排列,有
种不同的“排列”方法,再将捆绑后的元素与1、3、5、7进行全排列,有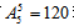 种方法,根据乘法原理共有6×120=720种不同的排法,所以共有720个符合条件的七位数,故选择B项。
种方法,根据乘法原理共有6×120=720种不同的排法,所以共有720个符合条件的七位数,故选择B项。
小结:捆绑法:在解决对于某几个元素要求相邻的问题时,先整体考虑,将相邻元素视作一个大元素进行排序,然后再考虑大元素内部各元素间顺序的解题策略。
【例题3】某学习平台的学习内容由观看视频、阅读文章、收藏分享、论坛交流、考试答题五个部分组成。某学员要先后学习完这五个部分,若观看视频和阅读文章不能连续进行,则该学员学习顺序的选择有多少种?( )
A.96 B.72 C.24 D.120
【答案】B【解析】由题意可得,观看视频和阅读文章不能连续进行,故可以采用插空法,首先考虑另外三个元素,有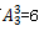 ,这三个元素会形成4个空,然后从这4个空中选出2个安排观看视频和阅读文章,则有
,这三个元素会形成4个空,然后从这4个空中选出2个安排观看视频和阅读文章,则有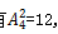 属于分步过程,所以总的有6×12=72种,故本题选B。
属于分步过程,所以总的有6×12=72种,故本题选B。
小结:插空法:插空法就是先将其他元素排好,再将所指定的不相邻的元素插入它们的间隙或两端位置,从而将问题解决。








