政华教育

首先我们要清楚什么样的题目可以考虑用整除，三方面入手。第一，题目中的名词在我们日常生活中以整数出现，比如人数，树的棵树等；第二，出现“整除”，“平均”，“每”等字眼，比如全班人数平均分成5组，则总人数能被5整除；第三，出现分数，小数，百分数，比如全班人数中女生占比3/5，则女生的人数能被3整除。接下来从具体的题目出发，详细给大家介绍。

例1：某知名饮食连锁店进行工作人员调整，在A、B两家店面中，A店员工人数是B店员工人数的2/3，如果从B店调6人到A店，则A店人数是B店的3/4，则两家店共有员工多少人（）？

A.200 B.210 C.220 D.230

【答案】B【解析】题目中出现名词为人数，我们知道人数一定是整数，且出现分数，考虑整除。根据题干“A店员工人数是B店员工人数的2/3”，则两家店员总人数能被2+3=5整除，观察选项无法排除；再根据题干“A店人数是B店的3/4”，则两家店员总人数能被3+4=7整除，观察选项只有B项满足，本题选择B项。

例2：某生产车间有若干名工人，按每四人一组分，多一个人；按每五人一组分，也多一个人；按每六人一组分，还是多一个人，该车间至少有多少名工人（）？

A.31 B.41 C.61 D.122

【答案】C【解析】题目中出现名词为人数，是以整数个出现的，且出现“每”，考虑整除。根据题干“每四人一组分，多一个人”，则总人数-1后能被4整除，同理总人数-1后也能被5和6整除，即总人数-1后是4、5、6的公倍数，求至少，则为最小公倍数60，本题选择C项。

通过例题我们也会发现，对于一些题目我们并不需要把题干全部都看完，抓住关键信息，根据整除进行分析，进而排除选项。当然如果有的题目只能排除2个选项的话，剩余选项我们可以代入到题干中，排除一个即可。

行测备考指导：空瓶换水如何换得“又快又准”

空瓶换水，是公务员考试经常涉及的一种统筹问题，重点考察考生的逻辑思维能力。尽管这类问题并不难，但考生往往因为粗心或考虑不周，没有做到“空瓶换最多的水”这一要求。那针对这种题目，如何做到效益最大化--即喝到最多的水呢，接下来将通过两道题分享一下解题思路。

例1：商店规定4个空瓶可以换1瓶矿泉水。现在有9个空瓶，请问最多可以免费喝多少瓶水（）？

A.4 B.3 C.2 D.6

【答案】B【解析】针对这道题目，我们可以通过平常思维来进行梳理：先拿8个空瓶换2瓶水，喝完之后算上原来1个空瓶，现在总共有3个空瓶。此时为了利益最大化，我们可以和别人“借”一个空瓶，凑成4个空瓶再换一瓶水，喝完之后再把剩下一个空瓶“还”给别人，也就是说9个空瓶最多可以喝到3瓶水。这种“有借有还”的思想，既能做到不亏欠，还使剩余3个空瓶最大化利用，即再换多一瓶水。

这道题目计算数值较小，仅有9个空瓶，但如果数值较大，比如算1000个空瓶最多换多少瓶水的话，这种列举形式虽然还能用，但是会显得非常繁琐复杂。在这里我们推荐一个简单方法帮大家计算。

我们可以把该题中条件“4个空瓶换1瓶矿泉水”可写成恒等式：

4个空瓶=1瓶水=1个空瓶+1“瓶”水

我们再将式子两边各消去1个空瓶而得：3个空瓶=1“瓶”水，也就是说9个空瓶可以换9÷3=3瓶水。

很明显，第二种解法才是在行测考题中比较快速、实用的方法。那我们接下来用这种方法尝试一道正常难度的例题。

例2：某啤酒品牌商家开展“7个空瓶换1瓶啤酒”的优惠促销活动。现在已知张先生在活动促销期间共喝掉347瓶啤酒，问张先生在花最少的钱的情况下，买了多少瓶啤酒（）？

A.297 B.298 C.290 D.302

【答案】B【解析】张先生共喝掉的347瓶啤酒中，有一部分是张先生自己花钱买的，还有另一部分是张先生用空瓶换的。

针对“7个空瓶换1瓶啤酒”的条件我们可以转化成：6个空瓶=1“瓶”啤酒。若假设张先生最少买了X瓶啤酒，根据6个空瓶=1份啤酒可得：347=X+X/6，解得X=297.4，但我们知道啤酒的瓶数必须是整数，因为最少是297.4瓶，瓶数取整就应该是298。综上本题选B。

以上就是关于空瓶换水换得“又准又快”的技巧，希望各位考生课后能够多积累复习，真正掌握解题方法。

行测数量关系：流水行船你不知道的“小秘密”

行程问题一直是数量关系中的重难点题型，很多考生望之生畏，其实考生只要找准方法，掌握做题技巧，这部分分值还是可以拿到的，今天就给大家介绍一种比较特殊的行程问题——流水行船。

特征

所谓流水行船问题，就是指船在江河里航行时，除了本身的前进速度外，还受到流水的推送或顶逆，在这种情况下计算船只的航行速度、时间和所行的路程。

公式

在流水行船问题中，有两个基本公式，如下：

顺水速度=船静水速度+水流速度

逆水速度=船静水速度-水流速度

(以下简称“船速”“水速”)

这两个公式很好理解，顺水速度快，逆水速度慢，已知一个公式里的任意两个速度都可以求出未知的第三个速度。如果已知顺水速度和逆水速度，由和差问题的解题方法，我们也可以求出船速和水速：

船速=(顺水速度+逆水速度)÷2

水速=(顺水速度-逆水速度)÷2

例1：船在静水中的速度为每小时13千米，水流的速度为每小时3千米，船从甲港顺流而下到达乙港用了15小时，从乙港返回甲港需要多少小时（）？

A.18 B.20 C.22 D.24

【答案】B【解析】由题意得，顺水速度为13+3=16千米/小时，逆水速度为13-3=10千米/小时，全程为16×15=240千米，返回所需时间为240÷10=20千米/小时。

例2：甲、乙两港相距360千米，一轮船往返两港需要35小时，逆流航行比顺流航行多花5小时，另一帆船每小时行12千米，这只帆船往返两港需要多少小时（）？

A.50 B.58 C.64 D.70

【答案】C【解析】要求帆船往返两港的时间，要先求出水速，轮船逆流与顺流的时间和与时间差分别是35小时与5小时。因此可求顺流时间和逆水时间，可求出轮船的逆流和顺流速度，由此可求水速。进而可求出另一帆船顺流速和逆流速，从而求得往返的时间。

轮船逆流航行时间为(35+5)÷2=20小时，轮船顺流航行时间为(35-5)÷2=15小时，轮船逆流速度360÷20=18千米/小时，轮船顺流速度为360÷15=24千米/小时，水速为(24-18)÷2=3千米/小时，帆船顺流速度为12+3=15千米/小时，帆船逆流速度为12-3=9千米/小时，帆船往返两港时间为360÷15+360÷9=64小时。

流水行船作为一个特殊知识点，要求广大考生需要掌握有效的备考方法以及快速识别题型特征的能力，同时还需要对各个知识点不断加强练习与巩固，合理安排自己的做题顺序与时间，希望这一部分的内容对大家的备考能有一定的帮助。

捆绑法安排“要挨着”的元素

在行测考试中，数量关系题目的难度众所周知，而其中排列组合问题的难度更是让人望而生畏，但却是近几年来的高频考点。解决排列组合问题的常用方法有优限法、捆绑法、插空法，今天带领大家一起深入研究捆绑法，看看有什么特点，使用时有什么注意事项。

方法介绍：当有元素要求相邻时，可先将要求相邻的元素进行捆绑视作一个整体，再与其它元素进行排序，最后再考虑要求相邻的元素内部是否也需排序。

一、要求相邻的元素，视作一个整体，即绑在一起当成一个大元素参与安排

例1：某高校在开学之际安排了5辆不同客车去4个车站接学生，要求每个车站至少去1辆车，则分配方案共有多少种（）？

A.24 B.48 C.96 D.240

【答案】D【解析】共5辆车对应4个车站，且每个车站至少1辆车，则一定有2辆车去同一个车站，那就可以看作2辆车相邻，5辆车中选出2辆，用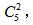将其视为一个大元素(即捆绑在一起)；此时相当于4个元素对应4个位置进行排序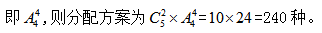，故本题选D。

二、将捆绑后的大元素与其他元素安排好后，考虑大元素内部的元素是否需要排序

例2：6名同事一起去看演出，预定了同一排相邻的6个座位，其中要求甲乙二人必须相邻而坐，则6人选择座位的情况一共有多少种（）？

A.120 B.240 C.480 D.720

【答案】B【解析】因甲乙二人要求相邻，可先将二人捆绑，视作一个大元素，捆绑后与其他4人排序，相当于有5个人进行排序，有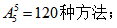而甲乙交换位置对结果有影响，所以甲乙内部有所求为2×120=240种。故本题选B。

三、可能会捆绑多次，依次考虑每个被捆绑后的大元素

例3：为加强机关文化建设，某市直机关在系统内举办演讲比赛，3个部门分别派出3、2、4名选手参加比赛，要求每个部门的参赛选手比赛顺序必须相连，问不同的参赛顺序的种数在以下哪个范围之内（）？

A.小于1000 B.1000-5000 C.5001-20000 D.大于20000

【答案】B【解析】因3个部门的选手比赛顺序必须相连，首先将每一个部门内部的人员进行捆绑看做一个整体，则3个部门的参赛顺序有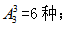其次考虑每一个部门内部选手的参赛顺序，分别有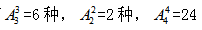。则不同参赛顺序的种数为6×6×2×24=1728种，故本题选B。

通过上面三道题目的讲解，相信大家对捆绑法有了更深一步的理解：遇到有“相邻元素”的问题，先把规定的相邻元素捆绑在一起参与安排；当需要考虑元素的内部排序时则对内部进行逐一排序，有多个被捆绑的大元素，则需要依次考虑。希望大家在今后的学习中能熟练掌握捆绑法。

多者合作不头疼，巧妙特值助你行

在行测考试中，多数同学对数量关系头疼不已，想要拿分，但总是有心无力，今天就来介绍一种好做易上手的题型：多者合作。

工程问题主要研究的是工作总量、效率、时间这三个量之间的基本数量关系，关系式为工作总量=效率×时间，而多者合作指一项工程由多个人或多种方式完成，让我们求具体其中一种方式的效率或所用时间。

这类题目具体应该如何解答呢？我们一起来看看。

一、当题目直接给出多个完工时间，特值工作总量为时间们的最小公倍数

例1：将A、B、C三个水管打开向水池放水，水池24分钟可以灌满；将B、C、D三个水管打开向水池放水，水池30分钟可以灌满；将A、D两个水管打开向水池放水，水池40分钟可以灌满。如果将A、B、C、D四个水管打开向水池放水，水池需多少分钟可以灌满（）？

A.22 B.18 C.15 D.20

【答案】D【解析】题目给出不同水管完成灌水用的时间，可设水池容量为120(24、30、40的最小公倍数)，使得效率为整数，则A、B、C三个水管的效率之和为120/24=5，,B、C、D三个水管的效率之和为120/30=4，A、D两个水管的效率之和为120/40=3，则A、B、C、D四个水管的效率之和为（5+4+3）/2=6。将A、B、C、D四个水管打开向水池放水，水池需120/6=20（分钟）可以灌满。本题选D。

二、当题目给出效率之比或者是有关效率的描述，可设效率为比例数

例2：甲、乙、丙三个工程队的效率比为6∶5∶4，现将A、B两项工作量相同的工程交给这三个工程队，甲队负责A工程，乙队负责B工程，丙队参与A工程若干天后转而参与B工程。两项工程同时开工，耗时16天同时结束。问丙队在A工程中参与施工多少天（）？

A.6 B.7 C.8 D.9

【答案】A【解析】题中给出甲乙丙的效率之比为6：5：4，可设甲、乙、丙效率分别为6、5、4，则A、B两项工程的工作总量为16×(6+5+4)=240，由于A、B工程的工作量相同，即为240÷2=120，在A工程中甲全程16天参与，即甲参与完成A的工作量为16×6=96，则丙在A工程参与施工(120-96)÷4=6天，选A。

三、出现多人/多物同时工作，可设每人/每物单位效率为“1”

例3：修一条公路，假设每人每天的工作效率相同，计划180名工人1年完成，工作4个月后，因特殊情况，要求提前2个月完成任务，则需要增加工人多少名（）？

A.50 B.65 C.70 D.60

【答案】D【解析】题目中给出多名工人一起修一条公路，设每名工人每月的工作量为1，则全部工作量为180×12×1，工作4个月完成工作量180×4×1。设要想提前2个月，则需要增加工人a名，则有180×4×1+(180+a)×(12-4-2)×1=180×12×1，解得a=60。本题选D。

通过以上讲解，希望大家在以后的考试中遇到工程问题时寻找做题的入手点，结合特值法，让工程问题成为自己的拿分点！