
行测数量关系备考技巧学习
单调性巧解数字推理
随着各省公告的陆续发布,2022省考备考行测已经迫在眉睫,而很多省份都会考察数字推理这种题型,我们如果不看特征去一个一个试加减乘除的规律,无疑会浪费掉很多的时间,下面教大家一个利用单调性解数字推理题目的好方法,让你化难为简。
一、具有单调性的数字推理
1.一般的数字推理题目往往具有单调递增或者单调递减的特征,这类具有单调性的题目若最大相邻两项变化幅度不大,最大相邻两项之间的倍数不超过2倍,则可以优先使用加减运算去考虑:
例题:2,5,8,11,14,( )
A.14 B.15 C.16 D.17
【答案】D【解析】本题所给数字单调递增,最大相邻两项倍数关系不到2倍,变化不大,可以优先使用加减运算。本题相邻两项之差为3,是公差为3的等差数列,故所求为14+3=(17)。
2.若最大相邻两项变化幅度较大,最大相邻两项倍数关系超过2倍,往往可以通过乘除或者多次方的角度去考虑:
例题:2,4,12,48,240,( )
A.960 B.1160 C.1440 D.2180
【答案】C【解析】本题所给数字单调递增,最大相邻两项(48,240)的倍数关系为5倍,变化较大,可以优先使用乘除运算。本题后项与前项作商依次为2、3、4、5、(6),故所求为240×6=(1440)。
二、不规则单调性的数字推理
除了上述具有规则单调性的数字推理外,往往还有很多题目单调性不规则,下面我们来看2类不规则单调性题目。
1.波浪型
波浪型指的是题目中的数字忽大忽小,像波浪一样起伏,这样的题目,往往可以优先考虑是组合数列、多次方数列。
例题:4,3,8,6,12,9,16,( )
A.5 B.12 C.14 D.21
【答案】B【解析】本题所给数字忽大忽小,呈现波浪变化趋势,且项数较多,所以可以优先考虑间隔组合或者分组组合数列。本题奇数项4,8,12,16是公差为4的等差数列;偶数项3,6,9,(12)是公差为3的等差数列。
2.抛物线型
抛物线型是指数字的大小变化先由小到大再由大到小,或者先由大到小再由小到大的变化趋势,这类不规则单调性优先考察多次方规律。
例题:1,32,81,64,25,( ),1
A.5 B.6 C.10 D.12
【答案】B【解析】数字由小到大再到小,呈现开口向下的抛物线型的变化规律,考虑使用多次方规律。本题是底数为1,2,3,4,5,(6),7,对应的指数为6,5,4,3,2,(1),0的多次方数。
通过规则单调性、不规则这两大类题型,相信大家对于数字推理题目也有一定的了解,但是行测要想快速地解题还是需要多练习,这样能提高做题速度,希望同学们勤加练习,多去积累,多做总结,相信大家在考试中看到数字推理题就可以从容应对。
行测数量关系简单公式之“快刀斩乱麻”
数量关系是公务员考试行测中的一部分,由于难度较大,往往做题时花费时间较多,其实有一部分题我们可以简化做题步骤,从而更加快速解题,为考试“加速”。通过数据之间的和差倍比,为大家介绍三种题型及其快捷公式。
1.和倍问题
问题描述:已知两数之和及倍数关系,可快速得出这两数。
快捷公式:大+小=和;大=倍×小
推出:小=和÷(倍+1);大=倍×小=和-小
例题:小张与小王同时从某地匀速慢走,两人速度和为40千米/时,且小张速度为小王的3倍,求两人各自的速度?
【解析】小张比小王大,小张与小王之和等于40,小张与小王的倍数=3;则得出:小王=40÷(3+1)=10千米/小时,小张=40-10=30千米/小时。
2.差倍问题
问题描述:已知两数之差及倍数关系,可快速得出这两数。
快捷公式:大-小=差;大=倍×小
推出:小=差÷(倍-1);大=倍×小=差+小
例题:小张比小王大10岁,小张是小王的2倍,则小张与小王各多少?
【解析】小张-小王=10,小张/小王=2;利用公式,则得出:小王=10÷(2-1)=10岁,则小张=10+10=20岁。
3.和差问题
问题描述:已知两数之和及两数之差,可快速得出这两数。
快捷公式:大+小=和;大-小=差
推出:大=(和+差)÷2;小=(和-差)÷2
例题:老张与侄子两人共60岁,老张比侄子大30岁,则他们俩各多少岁?
【解析】已知老张+侄子=60,老张-侄子=30;利用公式,则得出老张=(60+30)÷2=45岁;侄子=45-30=15岁。
希望考生们熟练掌握这部分公式,考试中遇到相应题目得以应用,为自己赢得时间,争取未来。
排队取水,先快后慢才完美
在公务员考试行测中,数量关系往往是令大多数考生头疼的一个部分,在大部分的情况下都是做不完的题型状态,但要想拿高分又不能放弃数量,所以我们需要在较短时间内尽可能多的做出几道较简单的数量题目。那么什么样的题目会比较简单呢?接下来为大家介绍一种简单的排队取水问题。
什么是排队取水问题
已知几个人到水龙头取水的时间不同,问这几个人取水时间加等待时间最短是多久?
排队取水问题的解题原则
让取水时间短的优先取水。
示例1:有甲、乙、丙、丁4人去水房打水,四人打水所需的时间分别为2、5、8、10分钟,若只有一个水龙头,要想4人打水和等待的时间之和最短,则最短时间为多少( )?
A.46 B.47 C.48 D.49
【答案】D【解析】由问题可知,要求4人打水和等待的时间之和最短。首先,4个人打水的总时间是不变的,共2+5+8+10=25分钟,所以只需让等待时间最短即可。而等待的总时间会随着先后安排的人员顺序的改变而变化,如果想要让等待的总时间最短,就需要让打水时间最短的人先打,打水时间长的后打。由此可得出按照甲、乙、丙、丁的顺序打水才能让总时间最短。甲先打2分钟,其他三人一共等待了3×2=6分钟;乙打水5分钟,剩下两人共等待了2×5=10分钟;丙打水8分钟,剩下一人共等待了1×8=8分钟。因此打水和等待时间之和最短为:25+6+10+8=49分钟。以上是将打水时间和等待时间分开计算再进行相加,但如果我们将打水和等待时间进行综合,即可直接列式为4×2+3×5+2×8+1×10=49分钟。
方法总结:第一步,确定打水顺序,让打水时间短的人先打,打水时间长的人后打;第二步,计算最短时间为n×a+(n-1)×b+(n-2)×c+……,(打水时间a<b<c......,n为打水人数)。
现在我们掌握了只有一个水龙头时排队取水问题的规律,那如果有多个水龙头又该如何解决呢?接下来我们再看下一道题。
示例2:7辆车要维修,一名工人修这7辆车分别需要12,17,8,18,23,30,14分钟,每辆车停开1分钟,经济损失11元。现由3名工效相同的维修工人各自单独工作,要使经济损失最小,至少要损失多少元( )?
A.1991 B.1178 C.619 D.181
【答案】A【解析】这个题目虽然不是描述排队取水,但由问题可知,要使经济损失最小,就要使总停产时间尽可能缩短,而停产时间由维修时间和车辆等待时间组成,7辆车总维修时间是不变的,所以只需让车辆等待时间最短即可。其实我们会发现,这里的维修时间就相当于“取水时间”,车辆等待时间就相当于“排队等待时间”,而工人就相当于“水龙头”。所以这个题目可以按照排队取水问题的规律解题。要想使车辆等待时间最短,显然应先修理修复时间短的车辆。由于三名维修工的效率相同,对每一个工人来说都应该是安排时间短的先维修,具体安排如下图所示(假设用ABCDEFG按照维修时间从少到多来表示这7辆车):
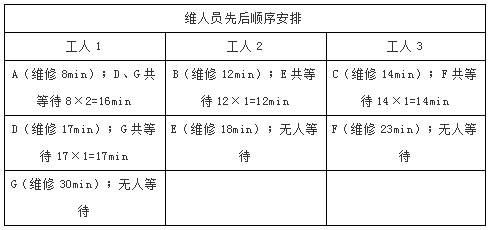
我们将维修和等待时间进行综合后可得到,最短时间列式即为3×8+2×17+1×30+2×12+1×18+2×14+1×23=181分钟,至少要损失181×11=1991元。
通过第二题可以发现,当出现多个“水龙头”时,我们的解题原则与一个水龙头是相同的,最后把各个水龙头时间相加即可。对于这种具有明显模型的题目,只要我们理解了基本原则就可以快速的解决这一类问题。
掌握“特值”,多者合作迎刃而解
在最近几年的公务员考试行测卷中,有一类题型容易被大家忽视,即:工程问题中的多者合作问题。大家总是潜意识里畏难,觉得未知量很多不敢下手。其实,此类问题是一组极为有规律的题型,难度并不大,只要掌握了其中的规律,解题就变得轻松很多。下面便为大家介绍多者合作问题的基本题型和解决这类问题的一种简单快速的方法——特值法。
多者合作,顾名思义就是多个元素(人或者机器)一起合作去完成某件事情,其中效率之间可以加和的一类问题。主要有三种设特值的方法:设工作总量、设工作效率和设每个元素单位时间内的工作量为1。
一、设工作总量
方法技巧:若题干中给出了完成某项工程的若干时间,设工作总量为1,进而表示工作效率。
例1:有一项工作,甲单独做需要10小时完成,乙单独做需要15小时完成。那么如果两人合作完成这项工作需要多长时间( )?
A.4小时 B.5小时 C.6小时 D.7小时
【答案】C【解析】设工作总量为1,则甲的工作效率为1/10,乙的效率为1/15,两人合作完成的时间为工作总量除以效率和,即: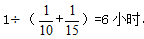 。
。
二、设工作效率
方法技巧:若题干给了多者之间的工作效率之比或者可以由题干推导出工作效率之间的比值关系,设工作效率为最简比,进而表示出工作总量。
例2:甲工程队与乙工程队的效率之比为4:5,一项工程由甲工程队先单独做6天,再由乙工程队单独做8天,最后由甲、乙两个工程队合作4天刚好完成,如果这项工程由甲工程队或乙工程队单独完成,则甲工程队所需天数比乙工程队所需天数多:( )
A.3天 B.4天 C.5天 D.6天
【答案】C【解析】设甲的效率为4,乙的效率为5,则这项工程的工作总量W=4×6+5×8+(4+5)×9=100。甲单独完成的时间为工作总量除以甲的效率,即:100÷4=25;乙单独完成的时间为工作总量除以乙的效率,即:100÷5=20。所以甲单独完成天数比乙要多:25-20=5天。
三、设每个元素单位时间内的工作量为1
方法技巧:若题干涉及到多个效率相同的元素(人或机器)合作,往往将每元素单位时间内的工作量设为值1,即直接用元素的数量代表工作效率。
例3:建筑公司安排100个工人去修某条路,工作2天后抽调走30人,又工作5天后再抽调走20人,总共用时12天修完。如果希望这条路在10天修完,且中途不得增减人手,则要安排多少名工人( )?
A.80人 B.90人 C.100人 D.120人
【答案】A【解析】由题意可以设每个工人单位时间内完成的工作量为1,则工作总量W=100×2+(100-30)×5+(100-30-20)×(12-2-5)=800,则要想10天完成工作,需要工人800÷10=80个。
通过以上介绍,相信各位同学已经掌握工程问题关于多者合作的这一考点,希望各位同学多加练习并熟记方法,在考场中游刃有余。








