行测数量关系解题技巧

行测数量关系：当一元二次函数极值遇上零点

回忆懵懂的初中学生时代，各位都曾经学习过一元二次函数，但是在随着时间长河的涓涓流淌，曾经记得很熟的知识也被不断地慢慢遗忘，而一元二次函数也是公务员考试中的一个知识点。接下来，一起来唤醒记忆深处那曾被遗忘的内容。

理论铺垫

对于一元二次函数，需要了解到其图像是关于对称轴对称的抛物线，并且最值是在对称轴位置取得。一元二次函数表达式有一般式、顶点式和零点式等多种表达式，而在考试中主要是针对零点式的考查，所谓的零点式是什么呢？

零点式指的是形如y=ax²+bx+c(a≠0)(a、b、c是常数)的函数，若y=0有两个实根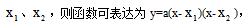此表达式即为零点式，同时抛物线与x轴有交点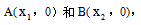这两个点即为零点，而零点是关于对称轴对称的，所以y的最值在对称轴取得。

对于使用零点法解决一元二次函数的步骤为：

第一步：通过观察二次项的系数a，确定抛物线开口方向。若a>0，抛物线开口向上，有最小值，没有最大值(建议删掉)；若a<0，抛物线开口向下，有最大值，没有最小值(建议删掉)。

第二步：令y=0，得出两个实根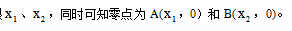

第三步：通过零点坐标得出对称轴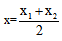，将x数值代入函数式得出y的最值。

例题1：某商品的进货单价为80元，销售单价为100元，每天可售出120件。已知销售单价每降低1元，每天可多售出20件。若要实现该商品的销售利润最大化，则销售单价应降低的金额是：（   ）

A.5元      B.6元      C.7元           D.8元

【答案】C【解析】所求为销售利润最大化，题干中给出的条件为进价、售价和销量，可以利用公式：总利润=(售价-进价)×销量，表达出数据之间的关系，不妨设销售单价应降低的金额为x元，则每天多售出20x件，可得总利润y=(100-x-80)(120+20x)，得出零点式的一元二次函数表达式。

第一步：通过观察二次项的系数a=-20，a<0，抛物线开口向下，有最大值，没有最小值(建议删掉)。

第二步：令y=0，得出两个实根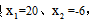同时可知零点为A(20，0)和B(-6，0)。

第三步：通过零点坐标得出对称轴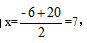即当销售单价降低7元时，得到销售利润最大值。故选择C项。

例题2：某苗木公司准备出售一批苗木，如果每株以4元出售，可卖出20万株，若苗木单价每提高0.4元，就会少卖10000株。那么，在最佳定价的情况下，该公司最大收入是多少万元？（   ）

A.60       B.80        C.90           D.100

【答案】C【解析】所求为销售收入最大化，题干中给出的条件为售价和销量，可以利用公式：总收入=售价×销量，表达出数据之间的关系，不妨设提高金额为0.4x元，则每天少售出x万株，可得总收入y=(4+0.4x)(20-x)，得出零点式的一元二次函数表达式。

第一步：通过观察二次项的系数a=-0.4，a<0，抛物线开口向下，有最大值，没有最小值(建议删掉)。

第二步：令y=0，得出两个实根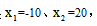同时可知零点为A(-10，0)和B(20，0)。

第三步：通过零点坐标得出对称轴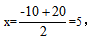即x=5时，得到销售收入最大值y=(4+0.4×5)×(20-5)=90万元。故选择C项。

通过上述例题的解析，各位对零点式的一元二次函数解题思路应该能有一个认识，需要依照对题干的理解整理出函数的表达式，然后利用解题步骤逐步推出即可。各位考生在以后做题中需要多加练习，熟练掌握。

行测排列组合题：回不到原来的位置了，怎么办

在行测里数量关系一直是困扰大家的难题，其中的排列组合更是答题路上的拦路虎。排列组合问题灵活性强，考点多，想要真正学好难度较大，但排列组合问题也有一些固定的模型，我们只要掌握了这些模型对于排列组合问题也是可以拿分的，今天就带大家来了解一下关于错位重排问题。

错位重排是伯努利和欧拉在错装信封时发现的，因此又称伯努利-欧拉装错信封问题。问题表述为：编号是1、2、...n的n封信，装入编号为1、2、...n的n个信封，要求每封信和信封的编号不同，问有多少种装法？(记n封信的错位重排数为)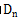

(1)若n=1，1封信对应1个信封，无法错位，故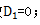

(2)若n=2，2封信对应2个信封，要实现错位，编号为1的信不能放入编号为1的信封，因此只能是编号为1的信放入编号为2的信封，编号为2的信放入编号为1的信封，有1种装法，故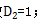

(3)若n=3，3封信对应3个信封，要实现错位，编号为1的信不能放入编号为1的信封，因此只能是编号为1的信放入编号为2或3的信封。若编号为1的信放入编号为2的信封，则编号为2的信只能放入编号为3的信封，编号为3的信放入编号为1的信封，此为第一种情况；若编号为1的信放入编号为3的信封，则编号为2的信只能放入编号为1的信封，编号为3的信放入编号为2的信封，此为第二种情况。因此，共有2种装法，故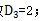

(4)若有n封信，n封信对应n个信封，要实现错位，编号为1的信不能放入编号为1的信封，因此只能是编号为1的信放入编号为2、3、4......的(n-1)个信封。若编号为1的信放入编号为2的信封，则编号为2的信有两种情况划分，一种是放入编号为1的信封，则剩余(n-2)封信不能放入(n-2)个信封中；另一种是不放入编号为1的信封，则剩余(n-1)封信不能放入(n-1)个信封中，因此，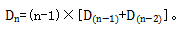

以上就是伯努利-欧拉装错信封问题的推导过程，从推导中我们会发现此过程是较为复杂且费时的。而在公务员考试行测试卷中，我们只需要能认出题目类型，会利用公式解答即可。接下来我们就来看看此类型的题型特征以及答题策略吧！

题型特征

错位重排是指元素本来有一一对应的位置，现在需要把元素的位置重新排列，使每个元素都不在原来位置上的排列问题。简单描述就是元素和位置的对应关系要重新排列且不能恢复原本的位置关系，求其方法的总数。

答题策略

错位重排原理很复杂，但是结论很简单，我们只需要记住结论就能快速解决这一问题。

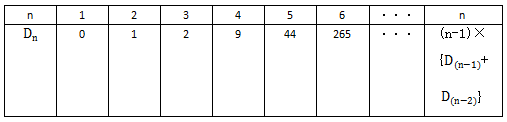
例1：编号1、2、3、4的四封信分别装入编号为1、2、3、4的四个信封，每封信要装入与自身不同编号的信封，问共有多少种装法？（   ）

A.2       B.6       C.9          D.12

【答案】C【解析】每封信要装入与自身不同的编号，也就是元素和位置的对应关系要重新排列，这一问题属于错位重排问题，4个元素的错位重排方法是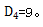

例2：编号1至6的六封信分别装入编号为1至6的6个信封里，每个信封放一封信，其中恰有2封信与信封的编号相同的方法有多少种？（    ）

A.9              B.35      C.135          D.265

【答案】C【解析】这道题目属于错位重排的复杂情况，6封信有2封信会放入对应编号的信封，有4封信会放入编号不对应的信封。首先，我们需要从6封信中挑出4封信放入编号不对应的信封，也就是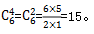接着，还需要考虑这四封信错位重排的方法数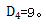，根据分步考虑使用乘法原理可知最终的结果是15×9=135。

例3：本周销售部的甲乙丙三名业务员分别从A、B、C三地出差归来，现需安排下周再去这三地出差的任务，若三人各去一地，但均不返回归来地的概率为(   )。

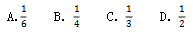
【答案】C【解析】三人各去一地出差的总样本数为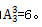三人均不返回归来地，说明元素和位置的对应关系要重新排列，且不能恢复原来的位置关系，属于错位重排，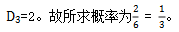

通过以上3个例题，我们发现只要清楚了错位重排这种题目的基本题型特征，在做题的时候直接应用其结论即可。同学们，记住表格里的常考数据以及基本公式了吗？记住了就去做做题，巩固一下！

空瓶到底换了几瓶水

行测数量关系一直是困扰大家的难题，其中的统筹问题更是题型变化多样，灵活性强，考点多，想要真正学好难度较大，但其中也有一些固定的模型，今天通过一些例题来了解一下统筹问题中的空瓶换水问题。

例1：3个矿泉水瓶可以换一瓶矿泉水，现有9个空矿泉水瓶，问不用买最多可以喝到几瓶水？（   ）

A.3      B.4       C.5          D.6

【答案】B【解析】第一步：9个空瓶子换3瓶水，首先喝到了3瓶水；第二步：3瓶水喝完以后剩下3个空瓶可以换1瓶水；第三步：换来1瓶水再喝完会剩下1个空瓶，1个空瓶不能进行更换。故一共喝了4瓶水。

例2：3个矿泉水瓶可以换一瓶矿泉水，现有10个空矿泉水瓶，问不用买最多可以喝到几瓶水？（   ）

A.3     B.4     C.5           D.6

【答案】C【解析】例二和例一问法一致，只是改变了空瓶数量，我们不妨再来推导一次。第一步：10个空瓶子换3瓶水，首先喝到了3瓶水；第二步：3瓶水喝完以后剩下3个空瓶加上最开始没有用的1个空瓶，此时有4个空瓶可以换1瓶水；第三步：换来1瓶水再喝完会剩下1个空瓶，加上之前没有用的1个空瓶共2个空瓶，此时我们手上只有两个空瓶按道理不能进行更换，但是我们可以向老板借一瓶水，把水喝了，现在就有3个空瓶再去换一瓶水就可以还给老板。故一共喝了5瓶水。

通过前两个题目我们发现这种利用空瓶换水的题目我们可以一步一步去推导，但是比较浪费时间，而且遇到例二这种题目我们还需要考虑借水问题，比较麻烦。而我们通过此类题目不难发现我们最后关注的是喝到了几瓶水，而不是换了几瓶水。那我们就可以把1瓶水=1份水+1个空瓶，根据题意，3个空瓶换1瓶水，可以看成3个空瓶=1瓶水=1份水+1个空瓶，通过化简，就得到了2个空瓶=1份水，我们现在再来利用这一规律解题：例一，9个空瓶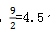，份水，向下取整就是4瓶水；例二，10个空瓶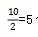，份水，所以喝了5瓶水，通过这样计算就简单很多。

所以针对空瓶换水类型的题目我们可以总结一个规律：如果A个空瓶可以换1瓶水，一共有B个空瓶，最多可以喝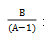瓶水。

通过以上两道例题相信大家对空瓶换水已经有了一定了解与认识，对于空瓶换水问题我们重点要掌握的就是换水的规律：如果A个空瓶可以换1瓶水，一共有B个空瓶，最多可以喝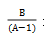瓶水。也就是说如果题目告知了空瓶子数量，我们可以直接套用规律；如果知道的是换水后喝到的水的数量，可以通过此规律列方程解题。那大家快去通过一些例题再巩固巩固吧！

行测数量关系日期问题知多少

日期问题是数学运算中的一类题型，这类题目与日常知识密切联系，理论知识并不难，更多是需要掌握相关结论并结合题型特点来解题，同时，能掌握一些运算技巧就更是锦上添花。接下来带大家一起整理汇总日期问题的相关结论并加之运用，解决此类问题。

认识常考日期

我们不妨按照时间概念的大小将常见的日期逐一整理。

1.年：分为平年和闰年，平年365天，闰年366天。

判定方法是“四闰百不闰，四百又闰。”也就是说，对于非整百年，该年是4的倍数即是闰年，对于整百年，通常不是闰年，除非是400倍数的年份，则也是闰年，其余都是平年。

2.月：分为大月和小月。

大月均是31天，分别有1月、3月、5月、7月、8月、10月、12月；小月除2月外其余是30天，分别有4月、6月、9月、11月，2月在平年是28天，闰年是29天。

3.星期：连续七天为一星期，即一周。

星期数问题本质是循环问题，其最小循环周期为7天，即每过7天，星期保持不变。则对于“求过n天的星期数”这类问题关键是看n除以7以后的余数是几，星期对应加几。比如：2021年8月2日星期一，问再过15天星期几？求解方法15除以7等于2余1，所以星期一加1即星期二。由此可得，每过一个大月，星期数加3；每过一个非2月的小月，星期数加2。

例1：已知2017年6月16日是星期五，那么2017年8月1日是星期几？（   ）

A.星期一   B.星期二      C.星期三      D.星期日

【答案】B【解析】星期数本质是以7天为一周期的循环问题，首先从6月16日开始，6月还剩14天，过14天星期数不变；7月有31天，星期数加3；8月1日星期数再加1。故星期五加4得到星期二，答案为B。

例2：已知2020年4月1日是星期四，那么10年后的4月1日是星期几？（   ）

A.星期一     B.星期二         C.星期三        D.星期四

【答案】B【解析】已知每过一个平年，星期数加1；每过一个闰年，星期数加2。从2020年4月1日到2021年4月1日是平年365天，其2月为2021年2月，28天。以此类推，这10年中共2个闰年，8个平年，所以在星期四的基础上加12，为星期二。故答案为B。

例3：如果某月里，星期五、星期六、星期日各有5天，那么该月的1日是星期几？（   ）

A.星期五     B.星期六         C.星期日        D.星期一

【答案】A【解析】对于一个月而言，一定包含完整的四周，即28天，也就是每个星期X都至少有4天，题中这月星期五、星期六、星期日均5天，说明本月有31天，最后的三天，29日、30日、31日分别为星期五、星期六、星期日。而所问该月1日其星期与该月29日星期一致，即星期五。故答案为A。

综上，是日期问题的相关理论和结论应用，难度不大，大家要注意的是常识理论记忆的精准性，尤其对于闰年的判定，很多考生的记忆是有偏差的，星期问题的个别题可能复杂，注意对其本质循环周期的理解和结论的应用，必要的时候也可以画图辅助理解。