政华教育

年龄问题在公务员考试行测试卷中是一类常考题型。这类问题经常会伴随着多个人在不同时间下年龄之间的关系，或是给出多人的年龄和。这类问题在日常生活中也经常遇到，主要考察大家的思维方式，相对来说，考法灵活，思维量小，难度系数一般，在考场上正常发挥就能解出结果。那么如何用正确的思考方式解决年龄问题，政华教育带大家去学习。

对于年龄问题主要包含的知识点有以下两点：

1、过了x年，一个人的年龄就长了x岁，同理，两个人的年龄和就长了2x岁。

2、无论两人的年龄如何变化，二者的年龄差始终是不会变的，如果发生变化了，意味着一方还未出生。

而在我们处理年龄问题的方法上，主要可以依据选项去代入排除，或者也可以通过题目中所给出的等量关系建立方程。接下来，让我们通过几个例题，来掌握年龄问题如何解决。

例题1：甲乙两人的年龄和是63岁，当甲是乙现在年龄的1/2时，乙当时的年龄是甲现在的年龄，乙比甲大几岁？（）

A.10 B.9 C.8 D.7

【答案】B【解析】设现在甲年龄为x岁，乙年龄为y岁。根据甲乙年龄和可得方程x+y=63，根据当甲是乙现在年龄的1/2时，乙当时的年龄是甲现在的年龄，由于年龄差不变，可得方程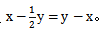解得x=27，y=36。故乙比甲大36-27=9岁。

例题2：小明和爷爷在做数学游戏，小明说：“我比弟弟大10岁，而且我比爷爷小我年龄的4倍”，爷爷和小明年龄的总和是弟弟年龄的18倍，问爷爷与弟弟年龄之和比小明年龄大多少岁？（）

A.65 B.60 C.62 D.58

【答案】A【解析】由题目条件可设小明的年龄为x岁，其弟弟为(x-10)岁，爷爷为5x岁，“爷爷和小明年龄的总和是弟弟年龄的18倍”可列式子x+5x=18(x-10)，解得x=15岁，故爷爷年龄为75岁，弟弟年龄为5岁，所求为75+5-15=65岁。

例题3：小强的爸爸比小强的妈妈大3岁，全家三口的年龄总和是74岁，9年前这家人年龄总和是49岁，那么小强的妈妈今年多少岁？（）

A.32 B.33 C.34 D.35

【答案】A【解析】一般情况下，三人今年的年龄之和是74岁，9年前三人的年龄之和应是74-9×3=47岁。现在已知9年前三人的年龄之和49岁，说明9年前小明是“-2”岁，即小明是在7年前出生的，今年7岁，则今年爸爸、妈妈年龄之和是74-7=67岁，爸爸比妈妈大3岁，则妈妈年龄是(67-3)÷2=32岁。

通过前面三个例题的讲解，大家对年龄问题的求解有了一定了解。年龄问题也没想象这么难，只要我们将生活中关于年龄的知识运用在其中，对于年龄问题的解决定是手到擒来。

行测数量关系：小小特值法，解决大问题

数量关系是行测考试中常考的一类题型，但同时又是考生们最头疼的部分。很多考生对数量关系题目都畏之如虎，但是这并不意味着数量题目无法入手，比如说行程、工程以及不定方程中在任意范围内求解的题型都可以通过设特值的方法去求解。下面带大家一起来学习一下它。

定义

通过设题目中某些未知量为特殊值，从而简化运算的方法。

应用环境

1.题目中存在具有任意性的量。

2.题目中的概念间存在A×B=M的关系，且要求出其中一个，而另外两个未知。

例题展示

(一)行程题目

例1：甲从A地到B地需要30分钟，乙从B地到A地需要45分钟，甲乙两人同时从A、B两地相向而行，中间甲休息了20分钟，乙也休息了一段时间，最后两人在出发40分钟后相遇。问乙休息了多少分钟？（）

A.25 B.20 C.15 D.10

【答案】A【解析】设AB的距离是90，则甲每分钟走90÷30=3，乙每分钟走90÷45=2，由于甲走了40-20=20分钟，走的距离为3×20=60，则乙走的距离为90-60=30，用时为30÷2=15分钟，所以乙休息了40-15=25分钟，故选A。

(二)工程题目

例2：某新建农庄有一项绿化工程，交给甲、乙、丙、丁4人合作完成。已知4人的工作效率之比为3∶5∶4∶6，甲、乙合作完成所需时间比丙、丁合作多9天，则4人合作完成工程所需时间是∶( )

A.17天 B.18天 C.19天 D.20天

【答案】D【解析】已知甲、乙、丙、丁工作效率之比为3∶5∶4∶6，设四人的效率分别为3、5、4、6，甲、乙合作完成所需时间为t天，则丙、丁合作完成的时间为t-9天，根据工作总量一定有(3+5)×t=(4+6)×(t-9)，解得t=45，工作总量为(3+5)×45=8×45，所求为8×45÷(3+5+4+6)=20天，故选D。

(三)不定方程题目

例3：现有甲、乙、丙三种货物，若购买甲1件、乙3件、丙7件共需200元；若购买甲2件、乙5件、丙11件共需350元。则购买甲、乙、丙各1件共需( )元。

A.50 B.100 C.150 D.200

【答案】B【解析】设购买甲、乙、丙各1件分别需花x、y、z元，则有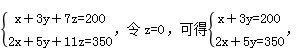上式×2-下式，可得y=50，代入上式可得x=50，因此所求x+y+z=50+50+0=100，即购买甲、乙、丙各1件需要100元，故选B。

以上就是关于用特值法去解决行程、工程以及不定方程的题目梳理，相信大家以后遇到同种类型题目的时候能想起用特值法去解决。

行测排列组合问题之切忌一条路走到黑

行测考试中，排列组合问题出现的频率近几年有增多的趋势，很多小伙伴却也为这样的题型头疼不已往往选择放弃，尤其是一些需要分成很多类去讨论的题目，费时费力的同时，一不小心还会有漏掉的情况，相对来说性价比并不高。排列组合确实是考试中的一个难点，今天政华教育带领大家一起学习排列组合中常用的一种方法间接法，用另一种视角进行分类求解。

知识点拨

在解决一些需要分类讨论的排列组合问题时，有的时候会发现正向求解要分类的情况非常多，比较复杂，我们可以用逆向思维去思考，看看其对立面的情况分类是否较少，那么我们就可以用总的方法数减去对立面的方法数即可得到我们所求的方法数，这样分类的情况和计算量都相应的减少了，这种解法我们称之为间接法。

例题：要从三男两女中安排两人周日值班，至少有一名女职员参加，有多少种不同的安排方法？（）

A.7 B.10 C.14 D.20

【答案】A【解析】方法一，包含两种情况，第一种为1名女职员1名男职员，第二种为2名女职员。第一种情况：1女1男，先从2名女职员中选择1名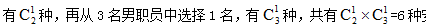，安排方法。第二种情况：2名女职员，有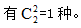分类相加，共有6+1=7种安排方法。

方法二，如果选的2人没有任何限制，从5人中选择2人共有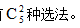种选法。而所求“至少有1名女职员参加”的对立面为“没有女职员参加”。没有女职员参加意味着两名男职员参加，从3名男职员中选择两名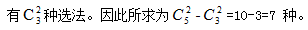，故本题选A。

小结

通过以上题目的练习，同学们能够发现间接法可以减少我们的计算量快速解决问题，那以后我们什么时候可以应用间接法呢？

特征：①正面分析时分类较多，而对立面的分类较少；②题干中出现“至多”，“至少”等字眼。

相信大家通过练习后再遇见此类题目，不要轻易放弃，可以尝试去做一做，希望对于大家的备考有所帮助。

行测指导：用“隔板法”轻松解决相同元素的分配

众所周知，在行测考试中，数量关系会出现排列组合问题，而对于这类问题，许多考生常常会觉得相对较难，而且还相对浪费时间，总认为排列组合都是复杂题。但是，在排列组合的题目中真实存在着一个题型，不仅解题的思维简单而且方法固定——那就是关于相同元素的分配问题。

对于相同元素分配给不同对象的过程中，首先，相同的元素不需要进行排列也不需要进行选择，其次，这类题型只需要对不同对象拥有的元素个数进行分类即可。最后，可以利用“隔板法”去完成所有的分配过程。接下来我们就结合例题详细说明如何操作。

例1：有8个完全相同的小球，想要放入一号、二号、三号盒子中，要求每个盒子中都至少有一个球，问满足条件的分配方式有几种？（）

A.28 B.21 C.15 D.10

【答案】B【解析】首先，题目满足相同元素分配给不同对象的题目特征。其次，我们可以利用“隔板法”在8个相同小球的内部，插入两个板，将小球分成三个部分，又因为在内部插板，所以能够满足每个部分都至少有一个球，将每个部分对应一个盒子的话，也就能够满足每个盒子都至少有一个的要求(如下图)。最后，我们需要在7个空隙中选择2个位置插板，因为空隙和空隙相同，而且插入的板和板之间也是相同的，所以不需要考虑顺序要求，直接用组合数所以选B项

例2：有8个完全相同的小球，想要放入一号、二号、三号盒子中，要求一号和二号盒子中都至少有一个球，三号盒子中至少有两个球，问满足条件的分配方式有几种？（）

A.28 B.21 C.15 D.10

【答案】C【解析】常规的“隔板法”能够满足的是每个对象都至少有一个元素，但是这道题想要三号盒子中至少有两个球，那可以从8个球里拿出一个先放入到三号盒子中，三号盒子现在也至少需要一个就能够满足要求。然后再利用“隔板法”在余下的7个球形成的不同空隙中选两个空插板(如下图)。同例1，不需要排序，所以直接所以选C项。

例3：有8个完全相同的小球，想要放入一号、二号、三号盒子中，要求一号和二号盒子中都至少有一个球，三号盒子中可为空，问满足条件的分配方式有几种？（）

A.28 B.21 C.15 D.10

【答案】A【解析】常规的“隔板法”能够满足的是每个对象都至少有一个元素，但是这道题想要三号盒子中可为空，那通过例2的经验可知，可先将三号盒子中的球从理论上先拿出一个球，放入到8个相同的球里，现在每个元素都满足至少有一个的条件。然后再利用“隔板法”在现有的9个球形成的不同空隙中选两个空插板(如下图)。同例1，不需要排序，所以直接所以选A项。

通过例题和练习的讲解，相信大家对“隔板法”的应用已经有所理解和掌握，那之后再做到关于相同元素分配给不同对象这类题目，就可以先将每个对象的数量要求转换成“每个对象至少有一个元素”这种模型，然后借用“隔板法”，在已有元素形成的内部空隙中插板来轻松解决。

希望今后大家多多练习，再次遇到此类题目能够快速准确地计算出结果。